Задача 3.4

Какую долю η кинетической энергии теряет нерелятивистская α-частица при упругом рассеянии под углом 60º в СЦИ на покоящимся ядре ¹²С?

Решение. Построим векторную диаграмму импульсов. ОтрезокАВ, изображающий импульс налетающей α-частицы, делим на 4 равных части, т.к.m_α:M(¹²С) = 1 / 3. От точкиАотсчитываем одну часть и ставим точкуО. Далее построения не отличаются от построений в предыдущей задаче.

Искомая доля будет равна

.

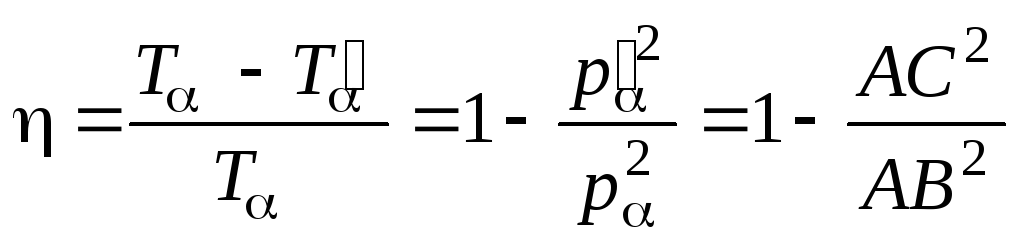Из треугольника АОС, используя теорему косинусов, находим

АС²= 1 + 9 – 2·1·3·cos(π-) = 1 + 9 + 3 = 13,

тогда

.

Рекомендуется получить формулу для вычисления η с произвольными углами .

Задача 3.5

Н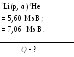айти энергию реакции⁷Li(p,α)⁴He, если известно, что удельная энергия связи в ядрах⁷Liи⁴Heравна соответственно 5,50 и 7,06 МэВ/нуклон.

Решение. Согласно (3.2)

Q=M(⁷Li) +m_p– 2М(⁴Не).

Используя формулу для полной энергии связи ядра:

ΔW(A,Z)= Zm_p + (A –Z)m_n – M(A,Z),

получим, что

Q = 3m_p + 4m_n - ΔW(⁷Li) + m_p – 2(2m_p + 2m_n – ΔW(⁴He)) =

= 2·ΔW(⁴He) – ΔW(⁷Li) = 2·4·– 7·=

= 8·7,06 – 7·5,60 = 17,3 МэВ.

Задача 3.6

Получить формулу (3.6).

Решение. Из формулы (3.3) для эндоэнергетической реакции (Q < 0):

|Q| = T1 –T2 = M2 – M1,

(3.6.1)

где Т₁ =T_а+T_АиМ₁=m_а+М_А,Т₂= T_b+T_BиМ₂=m_b+М_B, – суммарные кинетические энергии и суммарные энергии покоя частиц до и после реакции (3.1). Выражение (3.6.1) справедливо в любой инерциальной системе отсчета. Определим порог реакции как минимальное значение кинетической энергии (Т_а)_пор налетающей частицыав ЛСК (частицаАв ЛСК покоится!), при которой кинетические энергии образовавшихся частицbиВравны нулю в СЦИ. Для решения задачи удобно воспользоваться релятивистским инвариантом

Е²–p²с²=inv,

который сохраняется для любой изолированной системы в любой инерциальной системе отсчета. Здесь Е = М+Ти– полная энергия и суммарный импульс произвольной изолированной системы тел. Инвариант системы до реакции при пороговой энергии (Т_а)_порв ЛСК

inv1 = [M1+ (Та)пор]2 – ,

(3.6.2)

но

+ m_а²=[m_а+ (Т_а)_пор]²,

откуда

= + 2m_а·(Т_а)_пор.

Подставляя полученное выражение в (3.6.2) и выполняя необходимые преобразования, получим:

inv1 = .

(3.6.3)

В СЦИ инвариант для частиц с энергией покоя М₂, образовавшихся в результате эндоэнергетической реакции, будет равен:

inv2 = ,

(3.6.4)

т.к. их суммарная кинетическая энергия в СЦИ при пороговой кинетической энергии (Т_а)_порравна нулю.

Приравнивая инварианты (3.6.3) и (3.6.4), получим

(Та)пор=(M22 – M12)/ 2MА = (M2 – M12) (M1+ M2) / 2MА= = (M2 – M1) (M1+ M2 + M1 – M1)/ 2MА = (M2 – M1)[2M1+ + (M2 – M1)]/2MА= |Q| +,

(3.6.5)

так как согласно (3.6.1) (M₂ –M₁) = |Q|. Полученное выражение является точным и справедливо при любых скоростях налетающей частицыа. Но при |Q| < 100 МэВ второе слагаемое в (3.6.5) ничтожно мало по сравнению с первым и поэтому нерялитивистское приближение имеет вид:

.

(3.6.6)

Однако второе слагаемое в (3.6.5) становиться значимым при расчете пороговой энергии ядерных реакций, приводящих к рождению барионов и гиперонов.

Решим эту же задачу для нерелятивистского случая, когда .

Запишем (3.6.1) в СЦИ:

,

(3.6.7)

где верхний знак «~» указывает на принадлежность к СЦИ, а по определению. Кинетическая энергияТ₁частицаиАв ЛСК ив СЦИ связаны следующим образом:

,

(3.6.8)

где

(3.6.9)

есть суммарная кинетическая энергия частиц аиА, движущихся в ЛСК со скоростью ,скоростью движения СЦИ относительно ЛСК.

Согласно принципу относительности Галилея скорости частиц в ЛСК и СЦИ связаны следующим образом:

,

(3.6.10)

т. к. в ЛСК.

Используя (3.6.10), запишем закон сохранения импульса

.

(3.6.11)

Поскольку суммарный импульс частиц аиАв СЦИ равен нулю, то , и тогда из (3.6.11) скорость движения СЦИ относительно ЛСК

.

(3.6.12)

Решая систему уравнений (3.6.8), (3.6.9), (3.6.12) и учитывая, что , получим связь междуТ₁ивнерелятивистскомслучае

.

(3.6.13)

Подставив из (3.6.13) в (3.6.7), получим выражение

,

(3.6.14)

которое совпадает с (3.6.6). Еще раз обращаем внимание, что выражения (3.6.6) и (3.6.14) приближенные и действительны только в нерелятивистских случаях.