Розділ 3. Основи теорії графів. Деякі алгоритми на графах.
3.1. Основні визначення.
Серед дисциплін та методів дискретної математики теорія графів (в першу чергу алгоритми на графах) знаходять найбільш широке вживання у програмуванні. Графи є досить зручною моделлю при розв’язанні багатьох важливих та складних задач, що пов’язані з багатьма напрямками людської діяльності (економіка, хімія, радіотехніка тощо). Графи тісно пов’язані з відношеннями, які, в свою чергу, можна повністю виразити через поняття множини (див. Підрозділ 1.2). Проте незалежне визначення графу як відношення є більш зручним введення спеціальних термінів та позначень спрощує викладання теорії та робить її більш зрозумілою. В цьому підрозділі даються основні визначення, що пов’язані з графами.
Як це не дивно, для поняття „граф” нема загальновизначенного єдиного означення. Різні автори називають „графом” дуже схожі, але все-таки різні об’єкти. Ми в основному будемо користуватися визначеннями з підручників [Бондаренко, Новиков].
Нехай
задані деяка непорожня скінченна множина
![]() (множинавершин)
та сукупність невпорядкованих пар
(множинавершин)
та сукупність невпорядкованих пар
![]() множини
множини![]() (елементи в
(елементи в![]() можуть повторюватися).Графом
(точніше неорієнтованим
графом)
можуть повторюватися).Графом
(точніше неорієнтованим
графом)
![]() називається пара
називається пара![]() .
Елементи множини
.
Елементи множини![]() називаютьвершинами
графа
називаютьвершинами
графа
![]() ,
а елементи з
,
а елементи з![]()
його ребрами.
Аналогічно визначаються
орієнтовані
графи (або орграфи),
у яких
його ребрами.
Аналогічно визначаються
орієнтовані
графи (або орграфи),
у яких
![]() складається з упорядкованих пар. Ребра
неорієнтованих графів позначатимемо
у круглих дужках, а орієнтованих
у квадратних.
складається з упорядкованих пар. Ребра
неорієнтованих графів позначатимемо
у круглих дужках, а орієнтованих
у квадратних.
Якщо в
![]() містяться однакові пари, то такі ребра
називаютькратними.
Ребра виду
містяться однакові пари, то такі ребра
називаютькратними.
Ребра виду
![]() називаютьпетлями.
Якщо граф не містить петель та кратних
ребер, то його називають простим.
Далі, якщо не буде сказано інакше, ми
розглядаємо лише прості графи. У таких
графах сукупність невпорядкованих пар
називаютьпетлями.
Якщо граф не містить петель та кратних
ребер, то його називають простим.
Далі, якщо не буде сказано інакше, ми
розглядаємо лише прості графи. У таких
графах сукупність невпорядкованих пар
![]() стає множиною, яку називають множиноюребер.
стає множиною, яку називають множиноюребер.
Як
правило, в графі
![]() ми будемо нумерувати елементи множини
вершин
ми будемо нумерувати елементи множини
вершин![]() .
У такому випадку одержимограф
із поміченими вершинами.
Якщо ребро
.
У такому випадку одержимограф
із поміченими вершинами.
Якщо ребро
![]() належить множині ребер
належить множині ребер![]() ,
то вершини
,
то вершини![]() та
та![]() називаютьсуміжними.
Також говорять, що вершини
називаютьсуміжними.
Також говорять, що вершини
![]() та
та![]() інцидентні
ребру
інцидентні
ребру
![]() та навпаки. Два ребрасуміжні,
якщо вони мають спільну вершину.
та навпаки. Два ребрасуміжні,
якщо вони мають спільну вершину.
Нехай
![]() та
та![]() .
Розглянемо чотири основні способи
задання цього графа:
.
Розглянемо чотири основні способи
задання цього графа:
а) діаграма графа. Вершини позначаються крапками або кругами із відповідними номерами; ребра лініями;
б) перелік вершин та ребер;
в) матриця
суміжності. Це квадратна
![]() -матриця,
в якій елемент
-матриця,
в якій елемент![]() -го
рядка та
-го
рядка та![]() -го
стовпця
-го
стовпця![]() дорівнює одиниці, якщо в
дорівнює одиниці, якщо в![]() існує ребро
існує ребро![]() ,
а у протилежному випадку
,
а у протилежному випадку![]() .
Зауважимо, що для неорієнтованих графів
матриця суміжності є симетричною
відносно головної її діагоналі.
.
Зауважимо, що для неорієнтованих графів
матриця суміжності є симетричною
відносно головної її діагоналі.
г) список.
Цей список складається з
![]() рядків, у рядку з номером
рядків, у рядку з номером![]() у зростаючому порядку перелічують
вершини, які є суміжними з вершиною
у зростаючому порядку перелічують
вершини, які є суміжними з вершиною![]() .
Для орграфів перелічують всі номери
вершин
.
Для орграфів перелічують всі номери
вершин![]() ,
для яких існує ребро
,
для яких існує ребро![]() .
.
Проілюструємо способи задання графів на наступному прикладі.
Приклад
3.1. Побудувати діаграму,
матрицю суміжності та список неорієнтованого
графа
![]() ,
у якого
,
у якого![]() та
та![]() .
.
-
діаграма графа

матриця суміжності
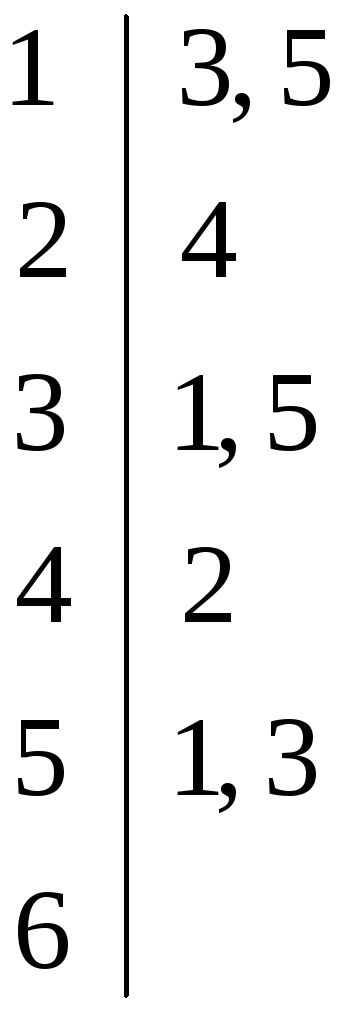
список ■
Рис. 3.1. Способи задання графа.
Степенем
вершини
![]() називається кількість ребер, інцидентних
цій вершині (позначається
називається кількість ребер, інцидентних
цій вершині (позначається![]() ).
Вершина степеня 0 називаєтьсяізольованою,
а вершина степеня 1
висячою.
).
Вершина степеня 0 називаєтьсяізольованою,
а вершина степеня 1
висячою.
Оскільки кожне ребро є інцидентних двом вершинам, то в суму степенів вершин графа кожне ребро входить двічі. Тому справедливе
Твердження
3.1. Сума степенів
вершин графа
![]() дорівнює подвоєній кількості його
ребер.
■
дорівнює подвоєній кількості його
ребер.
■
Виділимо
наступні види графів. Граф
![]() називаєтьсяпорожнім,
якщо всі його вершини є ізольованими
(тобто граф не має жодного ребра). Граф
називаєтьсяпорожнім,
якщо всі його вершини є ізольованими
(тобто граф не має жодного ребра). Граф
![]() називаєтьсяповним,
якщо будь-які його дві вершини суміжні.
Повний граф з
називаєтьсяповним,
якщо будь-які його дві вершини суміжні.
Повний граф з
![]() вершинами позначають
вершинами позначають![]() .
Для повного графа справедливе
.
Для повного графа справедливе
Твердження
3.2. Граф
![]() має
має![]() ребер.
ребер.
Доведення.
У повного графа
![]() степінь кожної з
степінь кожної з![]() вершин дорівнює
вершин дорівнює![]() .
Сума степенів графа дорівнює
.
Сума степенів графа дорівнює![]() .
З твердження 3.1 випливає, що граф
.
З твердження 3.1 випливає, що граф
![]() має
має![]() ребер.
■
ребер.
■
Граф
![]() називаєтьсядвочастковим,
якщо існує таке розбиття множини його
вершин
називаєтьсядвочастковим,
якщо існує таке розбиття множини його
вершин
![]() на дві підмножини (частки)
на дві підмножини (частки)![]() та
та![]() ,
що кінці будь-якого ребра графа належать
різним часткам. Двочастковий граф
називаєтьсяповним
двочастковим, якщо
будь-які дві його вершини, що належать
різним часткам, є суміжними. Повний
двочастковий граф, частки якого
,
що кінці будь-якого ребра графа належать
різним часткам. Двочастковий граф
називаєтьсяповним
двочастковим, якщо
будь-які дві його вершини, що належать
різним часткам, є суміжними. Повний
двочастковий граф, частки якого
![]() і
і![]() складаються відповідно з
складаються відповідно з![]() та
та![]() вершин, позначають
вершин, позначають![]() .
.
Маршрутом
або шляхом,
що з’єднує вершини
![]() та
та![]() називається скінченна послідовність
називається скінченна послідовність![]() вершин та ребер, у якій будь-які два
сусідні елементи є інцидентними один
одному. Оскільки ми розглядаємо лише
прості графи, то в маршрутах ми будемо
указувати лише вершини. Отже,маршрутом
у графі
вершин та ребер, у якій будь-які два
сусідні елементи є інцидентними один
одному. Оскільки ми розглядаємо лише
прості графи, то в маршрутах ми будемо
указувати лише вершини. Отже,маршрутом
у графі
![]() назвемо таку послідовність
вершин
назвемо таку послідовність
вершин
![]() ,
що всі пари
,
що всі пари![]() належать множині ребер
належать множині ребер![]() .
Число ребер у маршруті називають йогодовжиною.
Маршрут називають замкненим,
якщо його кінці співпадають (тобто
.
Число ребер у маршруті називають йогодовжиною.
Маршрут називають замкненим,
якщо його кінці співпадають (тобто
![]() ).
Маршрут, в якому всі ребра попарно різні
називаютьланцюгом,
а маршрут, в якому всі вершини попарно
різні (крім, можливо, кінців маршруту)
простим ланцюгом.
Замкнений ланцюг називається циклом,
а замкнений простий ланцюг
простим циклом.
Простий цикл довжини 3 називається
трикутником,
довжини 4
чотирикутником
і т.д.
).
Маршрут, в якому всі ребра попарно різні
називаютьланцюгом,
а маршрут, в якому всі вершини попарно
різні (крім, можливо, кінців маршруту)
простим ланцюгом.
Замкнений ланцюг називається циклом,
а замкнений простий ланцюг
простим циклом.
Простий цикл довжини 3 називається
трикутником,
довжини 4
чотирикутником
і т.д.
Граф називається зв’язним, якщо будь-які дві його вершини можуть бути з’єднані деяким маршрутом.
Введемо
деякі операції на графі
![]() .
.
Доповненням
цього графа називається граф
![]() ,
вершини якого ті ж самі, що і у
,
вершини якого ті ж самі, що і у![]() ,
та будь-які дві вершини графа
,
та будь-які дві вершини графа![]() суміжні тоді і тільки тоді, коли вони
несуміжні у
суміжні тоді і тільки тоді, коли вони
несуміжні у![]() .
.
Операція
вилучення вершини
![]() із графа
із графа![]() полягає у вилученні з множини
полягає у вилученні з множини![]() елемента
елемента![]() ,
а з множини
,
а з множини![]()
усіх ребер, інцидентних вершині
усіх ребер, інцидентних вершині
![]() .
Такий граф позначають
.
Такий граф позначають![]() .
.
Операція
вилучення ребра
![]() із графа
із графа![]() полягає у вилученні з множини
полягає у вилученні з множини![]() елемента
елемента![]() .
Такий граф позначають
.
Такий граф позначають![]() .
.
Операція
підрозбиття ребра
![]() у графі
у графі![]() полягає у вилученні з множини
полягає у вилученні з множини![]() елемента
елемента![]() ,
додавання до множини
,
додавання до множини![]() нової вершини
нової вершини![]() та додавання до множини
та додавання до множини![]() нових ребер
нових ребер![]() та
та![]() .
.
Два графа називаються гомеоморфними, якщо їх можна отримати з одного й того самого графа за допомогою підрозбиття його ребер.
Граф
![]() називаєтьсяпідграфом
графа
називаєтьсяпідграфом
графа
![]() і позначається
і позначається![]() ,
якщо
,
якщо![]() та
та![]() .
Якщо виконується
.
Якщо виконується![]() ,
то
,
то![]() називаютьвласним
підграфом графа
називаютьвласним
підграфом графа
![]() і позначають
і позначають![]() .
Іншими словами, якщо виконується
.
Іншими словами, якщо виконується![]() ,
то граф
,
то граф![]() є результатом виконання скінченої
кількості операцій вилучення ребер
та/або вершин з графа
є результатом виконання скінченої
кількості операцій вилучення ребер
та/або вершин з графа![]() .
.
Компонентою
зв’язності графа
називається максимальний зв’язний
підграф у графі. Так граф із приклада
3.1 має три компоненти зв’язності:
![]() .
.
Зв’язний граф без циклів називається деревом. Крім наведеного означення можна надати ще кілька еквівалентних визначень дерева.
Твердження
3.3. Для графа
![]() з
з
![]() вершинами та
вершинами та![]() ребрами рівносильні такі властивості:
ребрами рівносильні такі властивості:
1.
![]() зв’язний і не має циклів.
зв’язний і не має циклів.
2.
![]() зв’язний і кількість його вершин на
одиницю перевищує числа ребер:
зв’язний і кількість його вершин на
одиницю перевищує числа ребер:![]() .
.
3.
![]() не містить циклів та
не містить циклів та![]() .
.
4.
![]() не містить циклів та додавання ребра
між будь-якими несуміжними вершинами
призводить до появи циклу.
не містить циклів та додавання ребра
між будь-якими несуміжними вершинами
призводить до появи циклу.
5.
![]() зв’язний, але втрачає цю властивість
при вилученні будь-якого ребра.
зв’язний, але втрачає цю властивість
при вилученні будь-якого ребра.
6. Будь-які
дві вершини
![]() з’єднує єдиний ланцюг. ■
з’єднує єдиний ланцюг. ■
Остовом
(або
кістяковим
деревом)
зв’язного графа
![]() називається таке дерево
називається таке дерево
![]() ,
що є підграфом графа
,
що є підграфом графа
![]() ,
і множина вершин якого збігається з
множиною вершин
,
і множина вершин якого збігається з
множиною вершин![]() .
Більш детально про побудову кістякових
дерев графа будемо говорити у підрозділі
3.3.
.
Більш детально про побудову кістякових
дерев графа будемо говорити у підрозділі
3.3.
Графи
![]() та
та![]() називаютьсяізоморфними,
якщо існує таке взаємно однозначне
відображення
називаютьсяізоморфними,
якщо існує таке взаємно однозначне
відображення
![]() множини вершин
множини вершин![]() на множину вершин
на множину вершин![]() ,
що ребро
,
що ребро![]() належить
належить![]() тоді і тільки тоді, коли ребро
тоді і тільки тоді, коли ребро![]() належить множині ребер
належить множині ребер![]() .
Відображення
.
Відображення![]() називаєтьсяізоморфізмом.
Наявність ізоморфізму між графами
називаєтьсяізоморфізмом.
Наявність ізоморфізму між графами
![]() та
та![]() позначатимемо
позначатимемо![]() ,
а його відсутність
через
,
а його відсутність
через
![]() .
Справедливе таке очевидне
.
Справедливе таке очевидне
Твердження
3.4. Нехай
![]() ,
,![]() та
та![]()
деякі графи.
деякі графи.
Якщо
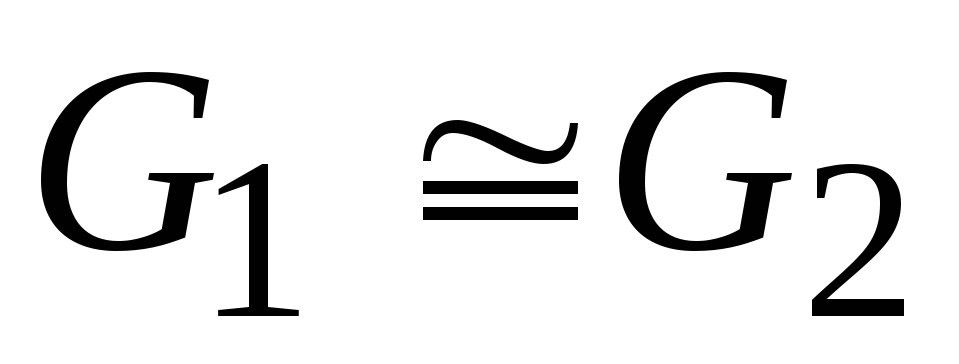 та
та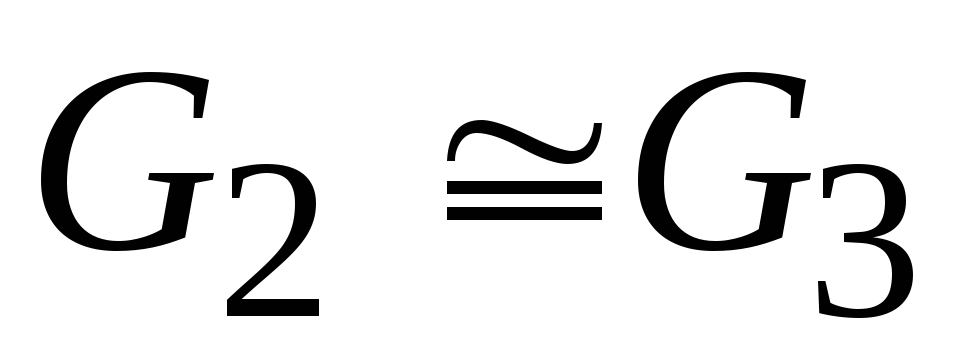 ,
то
,
то ;
;Якщо
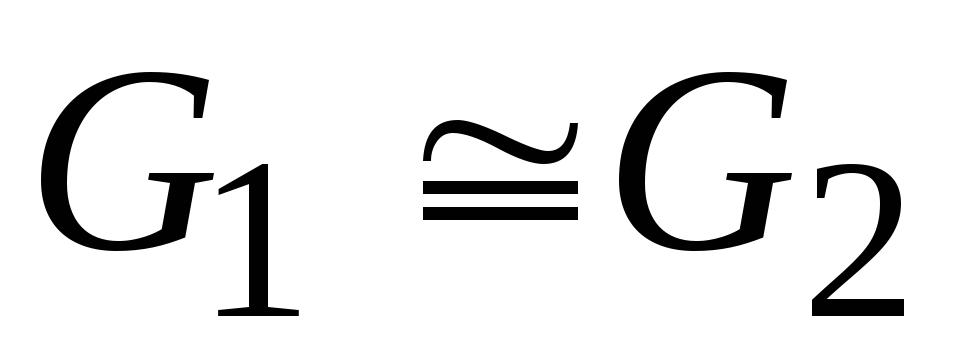 та
та ,
то
,
то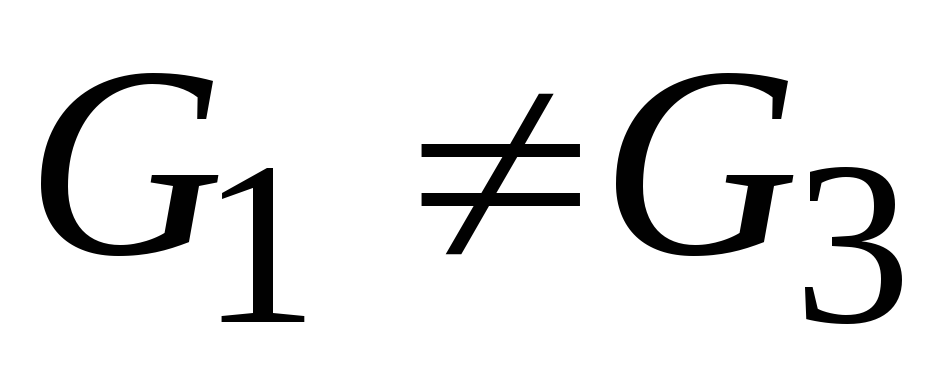 .
■
.
■
Зауважимо,
що у випадку
![]() та
та![]() наявність чи відсутність ізоморфізму
між графами
наявність чи відсутність ізоморфізму
між графами![]() та
та![]() невідома.
невідома.
Зрозуміло, що у ізоморфних графів однакова кількість вершин та ребер, однакова кількість вершин кожного степеня тощо. Проте невідомо жодного набору достатніх ознак, за якими можна сказати, що графи є ізоморфними.
На практиці визначення наявності ізоморфізму між графами є дуже складною задачею. До її розв’язання можна підійти наступним чином: вершини першого графу нумерують довільно, а вершини другого у відповідності із нумерацією вершин першого. Якщо для другого графу це можна зробити, то графи ізоморфні, а якщо можна довести, що цього зробити не можна, то графи не ізоморфні. Розв’язання цієї задачі значно полегшується у випадку, коли можна однозначно співставити хоча б одну вершину в обох графах.
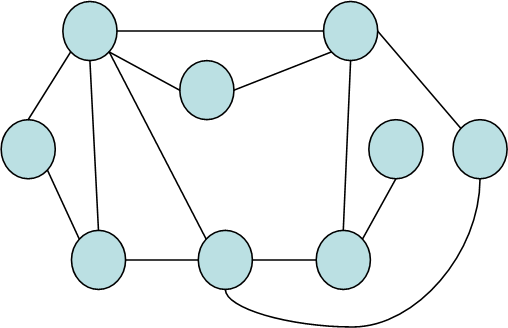
Приклад 3.2. Визначити, які графи з наведених на рис. 3.2. є ізоморфними між собою.
|
а) |
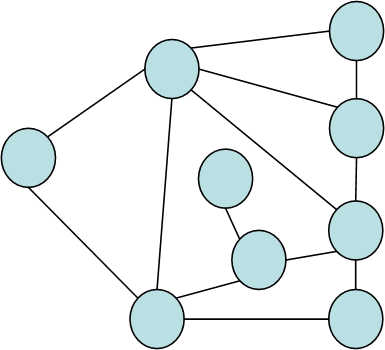
б) |
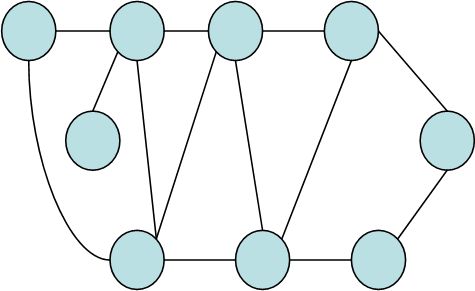
в) |
|
|
|
|
Рис. 3.2. Графи (а), (б) та (в).
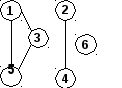
Довільним чином нумеруємо вершини графа (а).
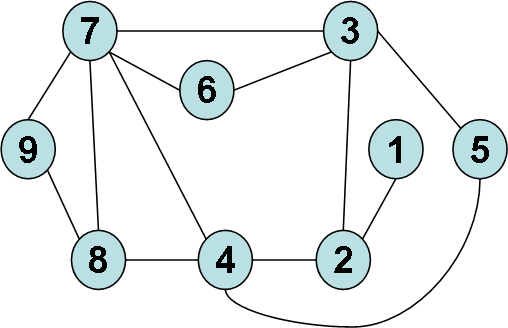
Рис. 3.3. Нумерація вершин графа (а).
У відповідності до цієї нумерації будемо нумерувати вершини графа (б).
Оскільки граф (б) має лише одну висячу вершину, то ми їй надамо номер 1. Ця вершина в графі (а) суміжна з вершиною 2, тому ми можемо однозначно надати номер 2 в графі (б):
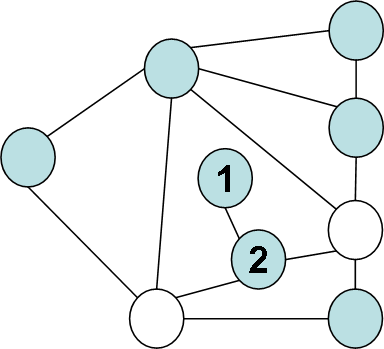
Рис. 3.4. Однозначна нумерація вершин 1 та 2 графа (б).
В графі (а) вершина 2 суміжна ще вершинам 3 та 4, які мають степінь 4. Такі самі вершини існують в графі (б) (вони виділені білим кольором). Треба з’ясувати яка вершини в графі (б) відповідають вершинам 3 та 4 графа (а). В графі (а) вершина 3 суміжна вершинам зі степенями 5, 3, 2, 2, а вершина 4 5, 3, 3,2. Тому ми можемо однозначно надати номери 3 та 4 виділеним вершинам графа (б).
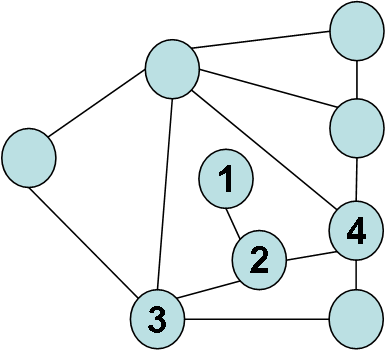
Рис. 3.5. Однозначна нумерація вершин 1, 2, 3 та 4 графа (б).
Тепер ми можемо однозначно надати номери 8 (суміжна з вершиною 4 та має степінь 3); 7 (суміжна з вершинами 3, 4 та має степінь 5); 5 (суміжна з вершинами 3, 4 та має степінь 2); 6 (суміжна з вершиною 3 та має степінь 2); 9 (суміжна з вершинами 7, 8 та має степінь 2):
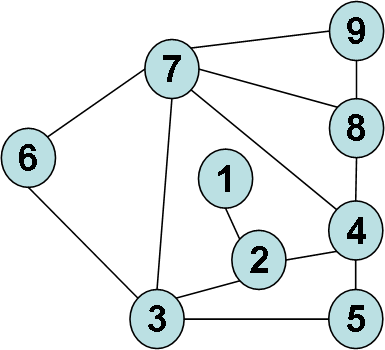
Рис. 3.6. Остаточна нумерація вершин графа (б).
Таким чином одержали, що граф (а) є ізоморфним графу (б).
Визначимо тепер, чи є ізоморфними графи (а) та (в). Вершини графу (а) нумеруємо так, як і в попередньому випадку. Так саме, ми можемо однозначно надати номери 1 та 2 вершинам графу (в):
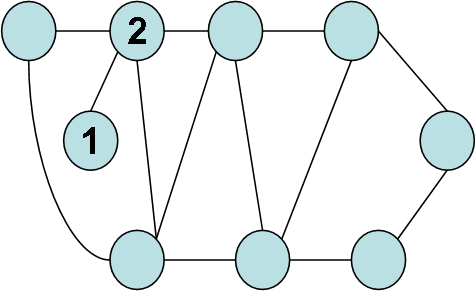
Рис. 3.7. Однозначна нумерація вершин 1 та 2 графа (в).
Проте в графі (а) вершина 2 має степінь 3, а у графі (в) степінь 4. Тому графи (а) та (в) не є ізоморфними.
Оскільки
![]() ,
та
,
та![]() ,
то за твердженням 3.3
,
то за твердженням 3.3![]() .
■
.
■
Виділимо ще один важливий вид графів.
Граф
![]() називається
планарним,
якщо його діаграму можна зобразити
(„укласти”) на площині чи сфері так,
щоб ребра перетиналися лише у вершинах.
Плоским
називається граф, діаграма якого містить
перетини ребер лише у вершинах. Таким
чином планарний граф є ізоморфним
деякому плоскому графу. На рис. 3.8 граф
(а) не є плоским, але є планарним, оскільки
він ізоморфний плоскому графу (б).
називається
планарним,
якщо його діаграму можна зобразити
(„укласти”) на площині чи сфері так,
щоб ребра перетиналися лише у вершинах.
Плоским
називається граф, діаграма якого містить
перетини ребер лише у вершинах. Таким
чином планарний граф є ізоморфним
деякому плоскому графу. На рис. 3.8 граф
(а) не є плоским, але є планарним, оскільки
він ізоморфний плоскому графу (б).

(а) (б)
Рис. 3.8. Приклад планарного та плоского графа.
Внутрішньою гранню плоского зв’язного графа називається скінченна область площини, що обмежена простим циклом та не містить жодного ланцюга, кінці якого належать цьому циклу. Крім внутрішніх граней кожний плоский граф має необмежену зовнішню грань. Так граф (б) з рис. 3.8 має три грані, з яких дві є внутрішніми (2 – 4 – 5 та 1 3 5 4).
Взаємозв’язок між кількістю вершин, ребер та граней плоского графа був знайдений Леонардом Ейлером у 1736 році:
Теорема
Ейлера для плоского графа.
Нехай плоский граф має
![]() вершин,
вершин,![]() ребер та
ребер та
![]() ребер. Тоді
ребер. Тоді![]() .
■
.
■
Важливим
наслідком теореми Ейлера є той факт, що
графи
![]() та
та![]() не є планарними.
не є планарними.
У 1927 році радянський математик Л.С. Понтрягін довів (але не опублікував) критерій планарності графа. Цей критерій незалежно від Л.С. Понтрягіна у 1930 році опублікував американський математик К. Кураторський.
Теорема
Понтрягіна-Куратовського.
Граф є планарним тоді і лише тоді, коли
він не містить підграф, гомеоморфний
![]() або
або![]() .
■
.
■