Сначала дописать это (окончание лекции)
6. Моменты распределения
Для подробного описания особенностей распределения используются дополнительные характеристики, в частности, определяются моменты распределения.
Моментами k-го порядка называется средняя из k степеней отклонений вариантов х от некоторой постоянной величины А:
При исчислении средней в качестве весов могут быть использованы частоты, частости и вероятности.
Эмпирические моменты – при использовании в качестве весов частот и частостей.
Теоретические моменты – при использовании вероятностей.
Порядок момента определяется величиной k.
Эмпирический
момент k-го
порядка определяется как отношение
суммы произведений k-х
степеней отклонений вариантов от
постоянной величины А
на частоты к сумме частот:
.
В зависимости от выбора постоянной величины А различают три вида моментов.
Условные
и начальные
относительно
моменты
(
)
получаются приА
равном некоторой произвольной величине
(начало отчета)
:
.
Этот вид момента применяется для
упрощения расчетов основных характеристик
ряда распределения.
2.
Начальные
моменты
(
)
получаются, еслиА
= 0:
.
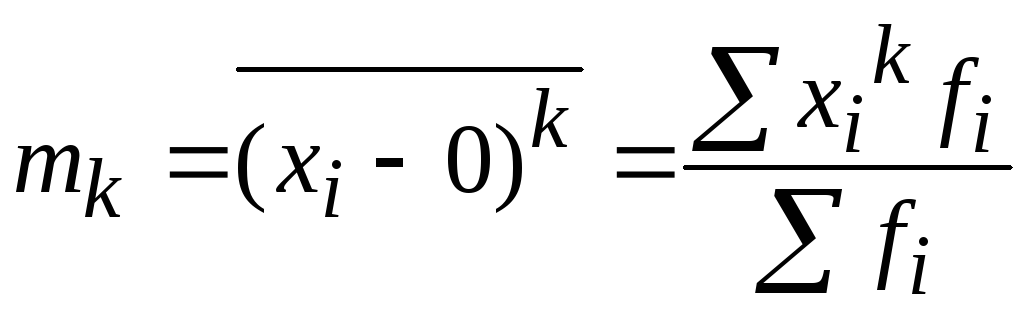(7.22)
3.
Центральные
моменты
(
)
получаются, если за постоянную величинуА
взять среднюю арифметическую (
):
.
(7.23)
Замечания:
А) в статистической практике пользуются в основном моментами 1-го, 2-го, 3-го и 4-го порядков;
Б)
начальный
момент 1-го порядка представляет собой
среднюю арифметическую и используется
как показатель центра распределения
(
);
В) начальные моменты 2-го, 3-го, 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов;
Г)
центральный
момент 1-го порядка всегда
равен нулю
=
0;
Д)
центральный
момент 2-го порядка представляет собой
дисперсию и служит основной мерой
колеблемости признака (
);
Е)
центральный
момент 3-го порядка служит мерой асимметрии
распределения, а если распределение
симметрично,
то он равен нулю (
);
Ж) центральный момент 4-го порядка применяется при вычислении эксцесса;
З) условные моменты 1-го, 2-го, 3-го, 4-го порядков не имеют самостоятельного значения, а используются для упрощения вычислений центральных моментов;
7. Изучение формы распределения
Для обобщающей характеристики особенностей формы распределения применяются кривые распределения.
Кривая распределения выражает графически (через полигон, гистограмму) закономерность распределения единиц совокупности по величине варьирующего признака (различают эмпирические и теоретические кривые распределения).
Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдений, в которой отражаются как общие, так и случайные условия, определяющие распределение.
Теоретическая кривая распределения – это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения
Кривые распределения могут быть одно-, двух- и многовершинными.
Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп. Для однородных совокупностей характерны одновершинные распределения. В следующих разделах рассмотрим одновершинные распределения.