
Асинхронные машины
.pdf
г) Начальный пусковой момент.
Вращающий момент при s = l называется начальным пусковым моментом. Его значение найдем, подставив в (3-129) s = l:
|
|
|
|
|
m U 2 r |
|
|
|
|
||
M |
|
|
|
|
1 |
1 |
2 |
|
|
|
|
нач |
ω [(r c r )2 |
|
(x |
c x )2 ] |
|
|
|||||
|
|
|
. |
(3-134) |
|||||||
|
|
1 |
1 |
1 |
2 |
|
1 |
1 |
2 |
||
|
|
|
|
|
|||||||
Уравнением (3-134) устанавливается зависимость Мнач = f( r2 ), которую мы будем рассматривать при изучении вопросов пуска в ход двигателей. Та же зависимость может быть получена из кривых рис. 3-44.
В предыдущем рассматривался электромагнитный момент, развиваемый ротором. При определении момента на валу нужно учесть механические (на трение) и добавочные потери, а также потери, вызванные пульсациями поля в зубцах статора и ротора. Практически электромагнитный момент мало отличается от полезного момента на валу, так как указанные потери незначительны.
3-14. Устойчивость работы машины
а) Двигатель.
Рассмотрим вначале вопрос об устойчивости работы трехфазного асинхронного двигателя. Напишем уравнение вращающих моментов, действующих на ротор двигателя при изменении его скорости вращения:
M M ст |
J |
dω |
M изб |
|
|
dt |
, (3-135) |
||||
|
|
|
где М — момент, развиваемый двигателем;
Мст — статический момент или момент сопротивления рабочего механизма, приводимого двигателем во вращение (с учетом потерь в самом двигателе);
J dω
dt — избыточный момент (положительный или отрицательный), обусловленный изменением кинетической энергии всех вращающихся частей двигателя и приводимого им во вращение механизма, имеющий общий приведенный к валу двигателя момент инерции J.
J dω |
|
Момент |
dt называется также динамическим или моментом сил инерции. Выражение для |
него может быть получено следующим образом: кинетическая энергия вращающихся частей равна
A J |
ω2 |
|
|
|
|
dA |
|
|||||
2 первая производная энергии по времени dt |
— мощность; мощность, деленная на угловую |
|||||||||||
|
||||||||||||
|
|
1 dA |
J |
dω |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
частоту, ω dt |
dt — динамический момент. |
|
||||||||||
|
|
|||||||||||
|
|
|
|
|
dω |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
При dt |
|
|
|
||||||||
|
|
и Мизб = 0, следовательно, М - |
Мст = 0. В этом случае двигатель работает с |
|||||||||
постоянной частотой вращения, момент двигателя М уравновешивается статическим моментом Мст, т. е М = Мст. Однако практически указанное равенство не может сохраняться длительно. Всегда возможны возмущения режима, которые вызовут изменения М или Мст и, следовательно, изменение
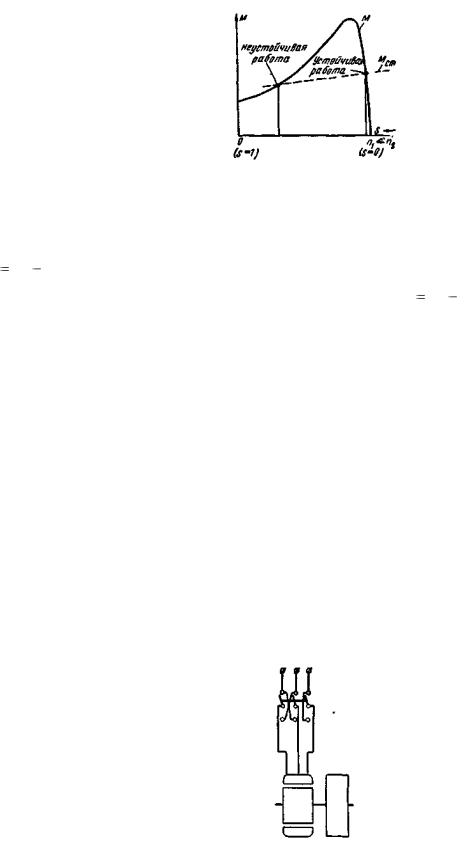
частоты вращения. Если по прекращении возмущения система (состоящая в данном случае из двигателя и механизма) стремится вернуться в исходное состояние и к нему возвращается, то она представляет собой устойчивую систему.
Обратимся к рис. 3-45, где представлена кривая момента двигателя M = f(n2). Она легко может быть получена из ранее приведенной кривой M = f(s), так как n2 = (1—s)n1. На том же рисунке приведена пунктирная кривая Mст = f(п2), соответствующая, например, изменению момента подъемного крана при изменении частоты вращения. Точки пересечения этой кривой с кривой момента двигателя получаются при равенстве М = Мст .
Рис. 3-45. К рассмотрению устойчивости работы асинхронного двигателя.
Правая точка соответствует устойчивой работе; здесь при возмущении, вызвавшем
положительное приращение частоты вращения, |
возникает отрицательный избыточный момент |
M изб M M ст , стремящийся замедлить вращение; при возмущении, вызвавшем отрицательное |
|
приращение частоты вращения, избыточный |
момент M изб M M ст будет положительным, |
ускоряющим вращение. В левой точке устойчивая работа невозможна, так как здесь при отклонении частоты вращения в любую сторону возникает избыточный момент, действующий в ту же сторону.
Следовательно, неравенство |
|
|||||||
|
dM ст |
|
dM |
|
dMст |
|
dM |
|
|
dn2 |
> dn2 или |
|
|||||
|
ds |
< ds |
(3-136) |
|||||
может служить критерием устойчивости работы. При соблюдении этого неравенства работа будет устойчивой, при несоблюдении его — неустойчивой.
б) Тормоз.
Обратимся к рассмотрению работы машины тормозом. Этот режим работы (при s > l) иногда применяется при необходимости быстро затормозить механизм, приводимый во вращение асинхронным двигателем. В этом случае применяется та же схема, что и при реверсировании двигателя (рис. 3-46).
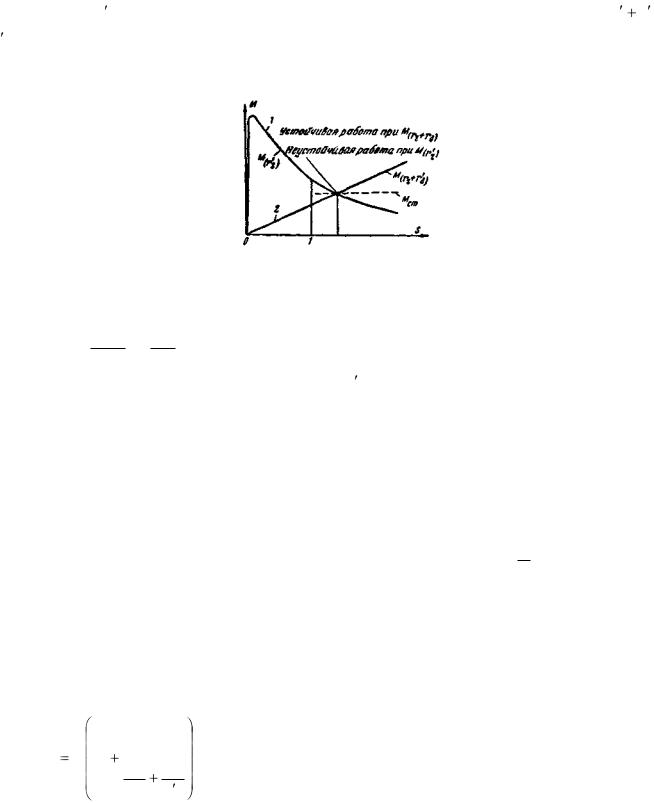
Рис. 3-46. Схема для реверсирования двигателя (изменения направления вращения) и для перевода его в режим работы тормозом (для сокращения времени выбега).
Для перевода машины в тормозной режим нужно изменить в ней направление вращения поля, что делается при помощи показанного на рис. 3-46 переключателя.
Если тормозной режим используется только для быстрой остановки машины, то устойчивость этого режима не имеет значения; но иногда требуется длительная работа машины в режиме тормоза, например в случае, когда рабочим механизмом является подъемный кран. Такая работа также должна быть устойчивой. На рис. 3-47 приведены кривые M = f(s): 1 — при обычном
сопротивлении r2 , обмотки ротора, 2 — при увеличенном сопротивлении цепи ротора r2 rд , где
rд — добавочное сопротивление (приведенное к обмотке статора), вводимое в цепь ротора; здесь же приведена кривая Mст = f(s) подъемного крана.
Рис. 3-47. Устойчивость работы машины в тормозном режиме.
Очевидно, только при второй кривой M = f(s) работа в тормозном режиме будет устойчивой, dMст dM
так как здесь ds < ds . Следовательно, для устойчивой работы тормозом нужно в цепь ротора
включить относительно большое сопротивление rд , что приводит также к уменьшению тока в обмотке ротора, а следовательно, и в обмотке статора.
3-15. Схемы замещения
Теория асинхронной машины основана на ее аналогии с трансформатором (§ 3-7 — 3-12). Необходимые величины и зависимости, характеризующие работу вращающейся машины, можно получить, заменив ее неподвижной машиной, работающей как трансформатор. При этом активное
r2
сопротивление роторной цепи, как указывалось, должно быть взято равным s .
На основе полученных ранее уравнений мы можем получить, так же как для трансформатора, схему замещения асинхронной машины, позволяющую легко найти соотношения между величинами, характеризующими ее работу.
Обратимся к уравнению (3-123) и перепишем его в следующем виде:
|
|
|
|
1 |
U1 |
I1 |
Z1 |
1 |
1 |
|
|
|
Z12 Z2s . (3-137)
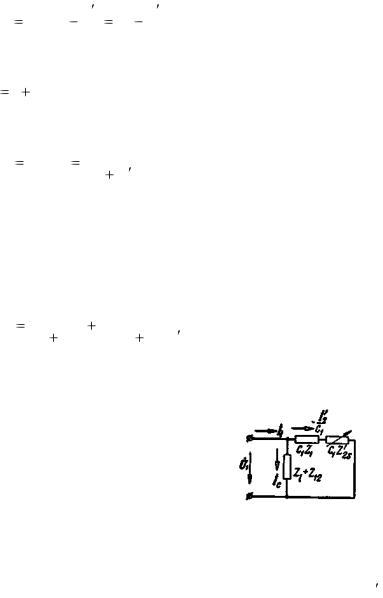
Выражению в скобках соответствует сопротивление схемы, приведенной на рис. 3-48.

Рис. 3-48. Схема замещения синхронной машины (Т-образная).
Уравнения напряжений и токов для этой схемы, составленные согласно законам Кирхгофа, будут такие же, как для машины [уравнения (3-115)— (3-117)]. Поэтому она называется схемой замещения асинхронной машины. Можем написать:
Z |
|
r2 |
|
jx2 r2 jx2 |
r2 |
1 |
|
s |
Z2 |
r2 |
1 s |
|
|||
2 s |
s |
|
|
|
|
s |
|
|
s |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
, (3-138) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Z2 |
r2 jx2 |
— сопротивление роторной обмотки при s = l. |
|||||||||||||
|
|
|
|
|
r |
1 |
|
s |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
s |
|
|
|
|
|
|
|
Активное |
сопротивление |
|
|
|
|
|
|
можно |
рассматривать как внешнее сопротивление, |
||||||
|
|
|
|
|
|
|
|||||||||
включенное в обмотку неподвижного ротора. Машина в этом случае работает как трансформатор,
имеющий чисто активную нагрузку. Электрическая мощность m1 I 2 2 r2 1 s s , отдаваемая таким
трансформатором, равна механической мощности P2 , развиваемой ротором при работе машины, например двигателем со скольжением s, что следует из полученного ранее равенства (3-70а) или (3- 100).
Можно вместо схемы рис. 3-48 получить схему, более удобную для исследования асинхронной машины, позволяющую составить простые расчетные формулы для токов, мощностей,
cos 1 и построить круговую диаграмму.
Из схемы рис. 3-48 следует:
|
|
|
|
|
|
1 |
|
|
U1 |
Z1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 0c |
(U1 - I1 Z1 ) |
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
||||||
|
Z12 |
|
Z12 |
Z12 . |
(3-139) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставив это значение I 0с |
в уравнение токов I1 |
I 0с |
I 0 , получим: |
|||||||||||||||||
|
U1 |
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I1 |
|
|
I1 |
|
|
|
|
I 2 |
|
|
|
|
|
|
|
|
|
|||
Z12 |
Z12 |
|
|
; |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсюда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 (1 |
|
) |
|
|
U1 |
I 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Z12 |
|
|
Z12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и
|
|
|
|
|
U |
1 |
|
|
|
I 2 |
|
|
I 2 |
|
|||
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
I c |
|
|
|
|
|
|
C1 Z12 |
|
|
C1 |
C1 , |
(3-140) |
||||||||||
|
|
|
|
|
|
|
|||||||||||
C1 |
|
1 |
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 |
|
|
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
[см. также (3-126)]; |
||||||||||||
|
|
|
|
|
U |
1 |
|
|
|
|
|
|
U1 |
|
|
|
|
|
I c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 Z12 |
|
|
|
Z1 |
Z 2 s . |
(3-141) |
||||||||
|
|
|
|
|
|
|
|||||||||||
— ток синхронизма, т. е. ток, потребляемый машиной при синхронной скорости вращения, при s = 0 (рис. 3-48).
Учитывая (3-141) и (3-127), перепишем уравнение (3-140) в следующем виде:
|
|
U |
1 |
|
|
|
|
U1 |
|
|
|
I c |
|
|
|
|
|
|
|
|
|
|
|
Z |
1 |
Z |
12 |
|
C Z |
|
C 2 Z |
2s . |
(3-142) |
||
|
|
|
1 |
1 |
1 |
||||||
Уравнениям (3-140) и (3-142) соответствует схема замещения, представленная на рис. 3-49.
Рис. 3-49. Г-образная схема замещения асинхронной машины.
Ее можно назвать Г-образной схемой замещения асинхронной машины. Она позволяет значительно проще, чем схема рис. 3-48, рассчитать токи I 2 и I1 при любом значении s, так как
здесь легко определяется ток I c , который не зависит от s. Исследование асинхронной машины при помощи приведенной на рис. 3-49 схемы замещения облегчается еще тем, что комплекс C1 в обычных условиях можно заменить его модулем с,. Только при точных исследованиях малых машин
(при Рн < 1 кВт) и в специальных случаях, когда аргумент γ1 в выражении С1 = c1e jγ больше 2—3°, следует его учитывать.
3-16. Параметры асинхронной машины
Параметры рассмотренных схем замещения являются в то же время параметрами асинхронной машины. Они могут быть определены расчетным или опытным путем.
При определении их расчетным путем нужно иметь геометрические размеры машины
(наружный и внутренний диаметры статора, то же для ротора, длину воздушного зазора δ между статором и ротором, их длины по оси, а также размеры пазов и зубцов статора и ротора) и ее обмоточные данные (числа витков, их средние длины, сечения проводников и шаги обмоток, числа пазов). Мы будем здесь рассматривать только основные методы расчета параметров, имея в виду установить их связь с геометрическими размерами машины и ее электромагнитными нагрузками.
Под последними понимаются индукции в отдельных участках магнитной цепи машины, линейная нагрузка (условная величина), А/см,

A 2m1w1 I1н
πD , (3-143)
плотности тока для статорной и роторной обмоток: 1 и 2 , А/мм2.
а) Ток холостого хода и сопротивление Z12.
Сопротивление Z12 ветви намагничивания (рис. 3-48) найдем, определив реактивную Iср и активную Iса составляющие тока синхронизма Iс.
Реактивная составляющая Iср, которая может быть названа намагничивающим током, практически равна реактивной составляющей Iор тока холостого хода. Для ее определения нужно
произвести расчет магнитной цепи машины, т. е. рассчитать н. с. F0 , могущую создать поток Ф, необходимый для наведения э. д. с. E1 0,97U1н .
Поток Ф находим по (3-77). По потоку Ф, зная сечения зубцов и ярм статора и ротора, определяем индукции в соответствующих участках магнитной цепи. Затем, пользуясь кривыми намагничивания для стали, из которой выполняется статор и ротор, находим для рассчитанных индукций напряженности поля и, умножая их на длины участков, находим магнитные напряжения этих участков.
Наибольшее магнитное напряжение приходится на воздушный зазор, максимальная индукция в котором
|
|
|
Bδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αδ |
ηl |
, |
(3-144) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
α |
δ |
|
0,7 |
(кривая |
поля вследствие насыщения |
главным образом |
зубцов статора и ротора |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
α |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
αδ |
0,7 ); l — длина статора по |
||
несколько отличается от синусоиды, поэтому вместо |
π берется |
|||||||||||||||
|
|
|||||||||||||||
оси за вычетом радиальных вентиляционных каналов. Для нормальных машин (от 0,6 кВт и выше)
Bδ 6500 8200 Гс.
Магнитное напряжение воздушного зазора
Fδ 0,8Bδ δkδ , |
(3-145) |
где kδ — коэффициент, учитывающий увеличение магнитного сопротивления воздушного зазора вследствие наличия пазов на статоре и роторе: его значение k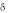 = 1,1÷1,5 (при открытых пазах оно больше, чем при полузакрытых).
= 1,1÷1,5 (при открытых пазах оно больше, чем при полузакрытых).
Магнитные напряжения стальных участков магнитной цепи при обычных насыщениях составляют в сумме примерно (0,2 0,5)F . Следовательно, мы можем написать:
F0 |
kн F , |
(3-146) |
|
|
где kн = 1,2÷1,5 — коэффициент насыщения. Такие значения для kн получаются, если индукции имеют обычные значения для зубцов — 14000 19000 Гс, для ярм — 10000 15000 Гс.
Согласно (3-59) и (3-146) реактивная составляющая

|
|
|
I0р |
Iср |
|
|
|
|
kн F p |
|
. |
|
|
||||||||
|
|
|
|
0,45m1w1k01 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
(3-147) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разделив обе части равенства на I1н, получим относительное значение |
|
|
|||||||||||||||||
|
|
|
I0р |
|
|
|
|
kн F p |
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1н |
|
0,45m1w1k01I1н |
|
(3-148) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
πD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p , то получим: |
||
|
|
Если сюда подставить (3-145) и учесть (3-143), а также равенство |
|||||||||||||||||||
|
|
|
I0р |
1,78 |
k |
н |
k |
|
|
|
|
B |
. |
|
|
|
|||||
|
|
|
I1н |
|
k01 |
|
|
|
|
A |
(3-149) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Уравнение (3-149) показывает, что относительное значение тока I0р зависит главным образом |
|||||||||||||||||||
|
δ |
|
|
|
Bδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
от η , так как A |
|
для нормальных машин колеблется в сравнительно небольших пределах. |
|||||||||||||||||||
При рассмотрении круговой диаграммы асинхронной машины (§ 3-17) мы увидим, что cos 1 двигателя зависит в основном от тока I0р. Поэтому для улучшения cos 1 воздушный зазор 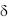 выбирается по возможности небольшим; при этом приходится считаться с необходимостью получить механически надежную машину, изготовление и установка которой не вызывают больших затруднений. Значения для нормальных машин приведены в табл. 3-4.
выбирается по возможности небольшим; при этом приходится считаться с необходимостью получить механически надежную машину, изготовление и установка которой не вызывают больших затруднений. Значения для нормальных машин приведены в табл. 3-4.
Та6лица 3-4. Воздушный зазор нормальных асинхронных машин
Мощность, |
До |
0,2- |
1,0- |
2,5- |
5- |
10- |
20- |
50- |
100- |
|
|
200- |
|
|
кВт |
|
0,2 |
-1,0 |
-2,5 |
-5 |
-10 |
-20 |
-50 |
-100 |
-200 |
|
|
-300 |
|
δ, мм при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3000 |
|
0,25 |
0,3 |
0,35 |
0,4 |
0,5 |
0,65 |
0,8 |
1,0 |
1,25 |
|
|
1,5 |
|
об/мин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ, мм при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1500 |
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
об/мин |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,4 |
0,5 |
0,65 |
0,8 |
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|||||||||||
|
Для тихоходных машин (при большом числе полюсов) величина η |
[см. (3-149)] больше, чем |
||||||||||||
для быстроходных (при малом числе полюсов). Этим и объясняется то, что тихоходные машины имеют более низкие значения cos 1.
Активная составляющая Iс.а тока синхронизма зависит главным образом от потерь в стали статора Pc1, вызванных основным полем, соответствующим главному потоку, и от электрических
|
m I 2 |
r |
(I |
c |
I |
ор |
) |
|
||
потерь |
1 |
ор 1 |
|
|
|
|
: |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
P |
|
m I |
2 |
r |
|
|
|
|
Iс.а |
|
с1 |
|
1 0р 1 |
. |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
m1U1н |
|
|
|
|
(3-150) |
|
|
|
|
|
|
|
|
|
|
|
|

Следовательно, ток синхронизма
Iс |
I02р |
Iс2.а . |
(3-151) |
|
|
|
Теперь мы можем рассчитать Z12 = r12 + jx12:
r |
|
Pс1 |
|
; x |
|
E1 |
; |
||
|
m I |
|
|
I |
|
||||
12 |
|
2 |
12 |
|
|
|
|||
|
|
1 с |
|
|
|
|
с.р |
|
|
|
|
|
|
|
|
|
|||
|
z |
|
r2 |
x2 . |
(3-152) |
||||
|
12 |
|
12 |
12 |
|
|
|||
|
|
|
|
|
|||||
Указанные параметры целесообразно выразить в относительных единицах, приняв, так же как
U1н
для трансформаторов (см. § 2-15), за базисную единицу сопротивлений I1н . Тогда получим, д.е.:
r* |
I1нr12 |
; |
x* |
I1н x12 |
. |
|
|
|
|
|
|
|
|
|
|
||||
12 |
U1н |
|
12 |
U1н |
|
|
|
|
|
|
|
|
(3-153) |
|
|
||||
|
|
|
|
|
|
|
|
||
Для нормальных машин значения |
r* |
x* |
r* |
||||||
12 и |
12 колеблются в следующих пределах |
12 = 0,5÷0,1 |
|||||||
д.е. (уменьшается с увеличением Рн и 2p), x12* = 4,5÷1,5 д.е. (уменьшается с увеличением 2р).
При определении тока холостого хода I0 нужно учесть еще его активную составляющую, соответствующую механическим потерям Рмех (на трение вращающихся частей о воздух, в подшипниках и щеток о контактные кольца, если они имеются), а также пульсационным и поверхностным потерям в зубцах ротора и статора Рс.д (при прохождении зубцов ротора под зубцами статора поле в них пульсирует с большой частотой, то же мы имеем для зубцов статора, кроме того, в сравнительно неглубоких поверхностных слоях зубцов ротора и статора получается неравномерное распределение поля из-за наличия пазов на противоположной части, изменяющееся при вращении ротора). Указанные потери покрываются за счет механической мощности, развиваемой ротором.
Таким образом, активная составляющая тока холостого хода
|
|
P |
P |
P |
m I 2 r |
|
|||
I0а |
|
с1 |
мех |
с.д |
1 0р 1 |
|
|
||
|
|
m1U1н |
, |
(3-154) |
|||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
где I0р |
I0 , и ток холостого хода |
|
|||||||
|
|
|
|
|
|
|
|
|
|
I 0 |
|
|
I 02р |
I 02а . |
|
(3-155) |
|
||
Для нормальных машин в обычных случаях (2p = 2 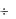 10)
10)
I0 100% (20 40)% |
|
|
I1н |
. |
(3-156) |
|
б) Активные сопротивления обмоток.
Сопротивление постоянному току фазы обмотки статора или фазного ротора рассчитывается,
Ом,
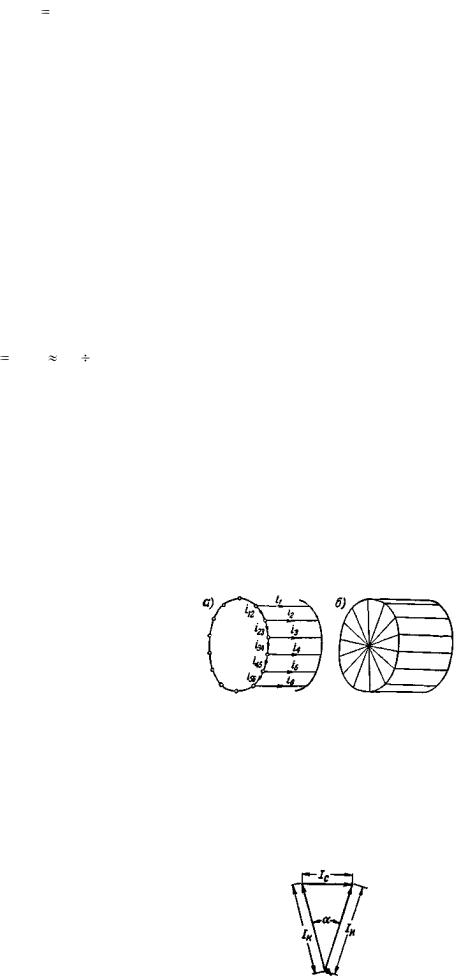
r ρ |
|
wlср |
|
|
75 |
sn |
а |
|
|
|
|
(3-157) |
||
|
|
|
|
|
где w — число последовательно соединенных витков;
а — число параллельных ветвей;
lср — средняя длина витка, м;
sn — сечение проводника, мм2.
Активное сопротивление r1 обмотки статора будет несколько больше рассчитанного по (3- 157). Оно должно учитывать не только потери от прохождения тока по обмотке, но и потери, вызванные полями рассеяния статора. Однако различие между активным сопротивлением и сопротивлением постоянному току обмотки статора обычно невелико и можно принять r1 = r, а потери, вызванные полями рассеяния, учесть отдельно при определении к.п.д. машины.
|
Значение |
сопротивления |
в |
относительных |
единицах |
измерения |
(о.е.) |
|
r * |
I1н r1 |
0,1 |
0,02 |
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
U1н |
соответственно при Рн = 0,4-7-600 кВт. |
|
Активное сопротивление r2 обмотки фазного ротора при нормальных режимах работы двигателя (при s < 5 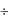 10%) может быть принято равным сопротивлению постоянному току. При больших скольжениях для двигателей, имеющих на роторе двухслойную стержневую обмотку (при глубине паза примерно свыше 2 см), r2 заметно возрастает.
10%) может быть принято равным сопротивлению постоянному току. При больших скольжениях для двигателей, имеющих на роторе двухслойную стержневую обмотку (при глубине паза примерно свыше 2 см), r2 заметно возрастает.
Покажем, как рассчитывается сопротивление r2 короткозамкнутой обмотки, выполненной в виде беличьей клетки. Такую клетку можно рассматривать как многофазную обмотку, имеющую число фаз m2, равное числу пазов ротора Z2, причем здесь в каждую фазу входит один стержень. На рис. 3-50,а схематически изображена обмотка в виде клетки.
Рис. 3-50. Беличья клетка и эквивалентная ей обмотка.
Здесь показаны токи в стержнях и частях короткозамыкающего кольца, лежащих между серединами соседних стержней. Эти части следует считать за сопротивления, соединенные многоугольникам. Поэтому токи в стержнях i1, i2, i3,… должны рассматриваться как линейные, а токи в частях кольца , i12, i23, i34,… — как фазные. В соответствии с этим на рис. 3-51 построена векторная диаграмма токов в соседних частях кольца Iк и в стержне Iс.
Рис. 3-51. Векторная диаграмма токов в стержне Iс и соседних частях кольца.
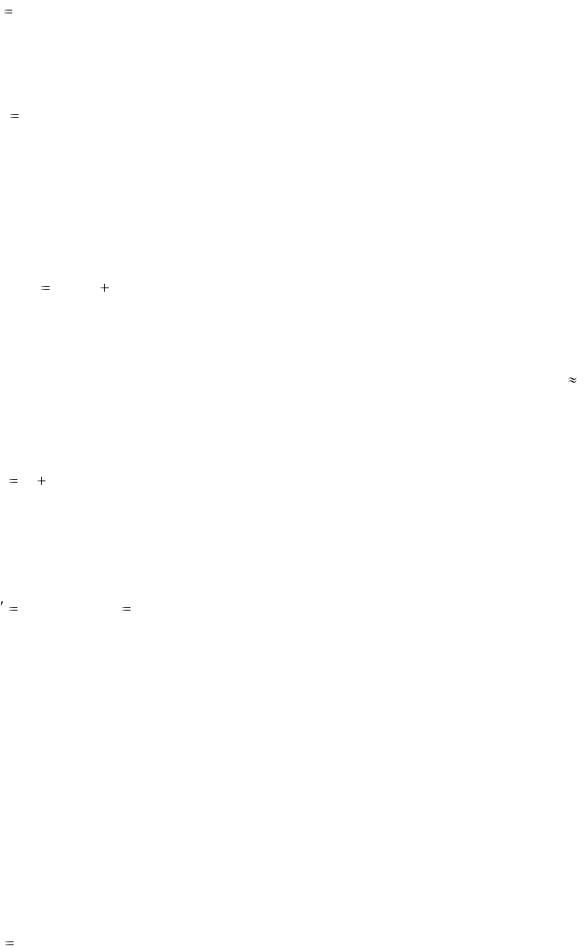
Сдвиг по фазе токов в соседних стержнях и частях кольца равен:
α |
2πp |
|
||
|
|
|
||
Z |
(3-158) |
|||
|
||||
|
2 . |
|||
Из векторной диаграммы находим соотношение между Iк и Iс:
I к I |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
с |
πp |
|
|
|||
|
|
2sin |
|
|||
|
Z 2 . |
(3-159) |
||||
|
|
|
||||
Для расчета заменим сопротивления частей кольца, соединенные многоугольником, сопротивлениями, соединенными звездой, после чего получим эквивалентную обмотку, показанную на рис. 3-50,б. Сопротивление фазы r2 такой обмотки принимается за сопротивление фазы беличьей клетки Оно определяется из равенства
Z |
|
I 2 r |
Z |
|
I 2 r 2Z |
|
I 2 r |
(3-160) |
|
2 |
с 2 |
|
2 |
с с |
2 |
к к , |
где rс — сопротивление стержня; rк — сопротивление части кольца между соседними стержнями. Сопротивления rс и rк определяются по геометрическим размерам стержня и кольца и удельному
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
||
сопротивлению материала, примененного для клетки (например, для литого алюминия |
|
23 . |
||||||||||||||||
Из (3-160) и (3-159) имеем: |
|
|
|
|
|
|
|
|||||||||||
r2 |
rc |
|
|
|
2rк |
|
|
|
|
|
|
|
|
|
|
|
||
|
(2sin |
πp |
) |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Z 2 |
. |
(3-161) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Приведение сопротивления r2 к обмотке статора делается по формуле |
|
|
|
|||||||||||||||
|
|
m |
w k |
01 |
|
2 r |
4m (w k |
01 |
)2 |
|
|
|
|
|
||||
r |
r |
1 |
( |
1 |
|
) |
1 1 |
|
|
|
|
|
|
|||||
2 |
2 m2 |
w2 k02 |
|
2 |
Z 2 |
|
, |
(3-162) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
так как m2 = Z2, w2 = 1/2, k02 = 1. Здесь также при малых скольжениях (s < 5 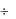 7%)r2, может быть принято равным сопротивлению постоянному току При больших скольжениях оно заметно возрастает, особенно при глубоких пазах на роторе (§ 3-19,в).
7%)r2, может быть принято равным сопротивлению постоянному току При больших скольжениях оно заметно возрастает, особенно при глубоких пазах на роторе (§ 3-19,в).
В обычных случаях значение r2 близко к значению r1.
в) Индуктивные сопротивления рассеяния обмоток.
Определение потокосцеплений рассеяния, а следовательно, и индуктивных сопротивлений рассеяния х1 и х2 представляет собой сложную задачу, точное решение которой не представляется возможным. Поэтому при практических расчетах довольствуются приближенными методами, достаточная точность которых подтверждается опытом.
Индуктивное сопротивление может быть представлено в следующем виде:
x ωL . (3-163)
