
Асинхронные машины
.pdf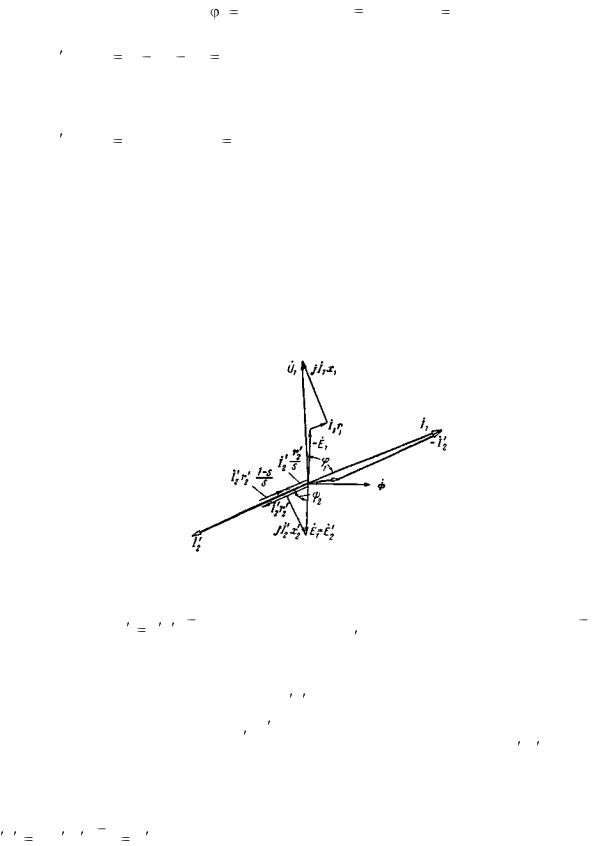
а отсюда, учитывая, что |
m U |
I |
1 |
cos |
P |
, |
m E I |
0c |
sin α |
P |
, |
m I 2 r |
P |
, будем иметь: |
||||
1 1 |
|
|
1 1 |
1 1 |
|
c1 |
1 1 1 |
э1 |
||||||||||
m E I |
|
cosψ |
|
P |
P |
|
|
P |
P |
|
(3-105) |
|
|
|
|
|
||
1 1 |
2 |
|
2 |
1 |
э1 |
|
|
с1 |
эм , |
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1E1I2 cosψ2 |
m2 E2 I2 cosψ2 |
Pэм . |
(3-106) |
|
|
|
|
|
||||||||||
3-11. Векторная диаграмма асинхронного тормоза
Векторная диаграмма н.с. машины, работающей тормозом, принципиально не отличается от диаграммы рис 3-31, так как при вращении ротора против поля (s>l) направление перемещения поля относительно проводников статора и ротора будет тем же, что и при работе машины двигателем.
Диаграмма временных векторов может быть построена для условного трансформатора (рис. 3-34) на основе тех же уравнений (3-98). Она представлена на рис. 3-36.
Рис. 3-36. Векторная диаграмма асинхронного тормоза (приведенного к работе трансформатором).
|
|
|
1 |
|
s |
1 |
s |
||||
U |
2 |
I 2 r2 |
|
s |
|
направлен против I 2 , так как при s > 1 величина |
|
s |
|
|
|
Здесь вектор |
|
|
|
|
|
|
|
является |
|||
отрицательной; следовательно, мы его должны рассматривать как вектор напряжения, приложенного извне к зажимам роторной цепи. Мы должны считать, что в роторную цепь включен внешний
источник |
энергии, |
мощность которого |
m1U 2 I 2 |
вводится в обмотку |
ротора, |
где |
расходуется на |
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
r2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
m1 I 2 |
|
|
|
|
2 |
|
|
|
электрические потери. Другая часть |
s полных электрических потерь m1 I 2 |
r2 в обмотке ротора |
||||||||||||||||
|
|
|||||||||||||||||
покрывается за счет мощности, передаваемой ротору со статора магнитным полем. |
|
|||||||||||||||||
|
|
Для |
|
|
|
вращающейся |
машины, |
работающей |
тормозом, |
мощность |
||||||||
m U |
I |
|
m I |
|
2 r |
1 |
s |
P |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 2 |
|
2 |
1 |
2 |
2 |
|
s |
|
2 является механической мощностью, подведенной извне к ее ротору. |
|||||||||
3-12. Асинхронный генератор и его векторная диаграмма
Работу асинхронной машины генератором (при s < 0) мы также можем привести к работе некоторого условного трансформатора.
Обратимся сначала к рис. 3-37, где приведена диаграмма пространственных векторов н.с. обмоток статора и ротора при работе машины генератором.
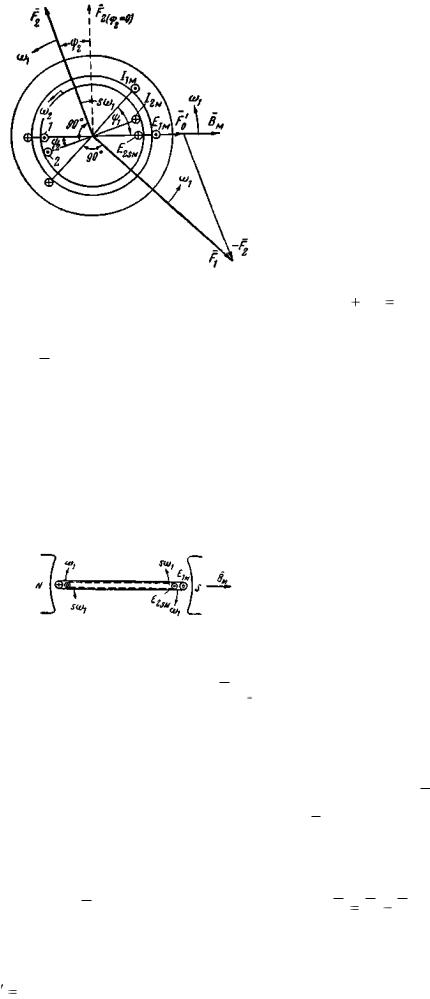
Рис. 3-37. Пространственная диаграмма н.с. асинхронного генератора ( sω1 ω2 ω1 ).
Здесь, так же как и для двигателя, принято, что в рассматриваемый момент времени
пространственный вектор индукции Bм , вращающийся с угловой частотой ω1 относительно статора, направлен по горизонтали.
На рис 3-37 показаны фазы статора и ротора, в которых наводятся максимальные э.д.с. E1м и
E2sм . Их направления найдены с учетом перемещения проводников фаз относительно поля. При ω1 < ω2 проводники фазы ротора перемещаются относительно поля в направлении, обратном перемещению относительно поля проводников фазы статора (рис. 3-38). Поэтому э.д.с. E1м и E2sм имеют взаимно противоположные направления.
Рис. 3-38. К определению направлений э.д.с. статорной и роторной обмоток при s < 0.
Если бы ток I 2 совпадал по фазе с э.д.с. E2s , то вектор F2( ψ2 0) совпадал бы с осью катушки 1
ротора, имеющей максимальную э.д.с. E2sм . Но вследствие наличия в роторной цепи индуктивного
сопротивления x2s ток I 2 отстает по фазе относительно E2s на угол ψ2. Поэтому максимальный ток I2м будет иметь место в катушке 2, где э.д.с. была максимальной ранее на промежуток времени,
соответствующий углу ψ2. Следовательно, в действительности (при ψ2 > 0) вектор F2 будет
совпадать с осью катушки 2. При ψ2 > 0 (при отстающем от э.д.с. токе) н.с. F2 смещается в сторону, противоположную вращению н.с. относительно ротора, но по отношению к статору она смещается в сторону вращения поля.
Намагничивающую силу статора F1 , найдем, исходя из равенства F1 F0 F2 . Отсюда найдем ту фазу статора, ток которой в данный момент времени имеет максимальное значение (рис.
F2 . Отсюда найдем ту фазу статора, ток которой в данный момент времени имеет максимальное значение (рис.
3-37).
|
|
|
|
|
I |
|
E |
|
Если допустить, что |
F0 0 |
и x2s = 0, то мы получили бы совпадение по фазе |
и |
; |
||||
|
|
|
1 |
1 |
||||
максимальный ток I1м был бы в той же катушке, в которой наводится максимальная .э.д.с. |
E1м . В |
|||||||
действительности |
F0 |
> 0 и x2s |
> 0, поэтому |
I |
и |
E |
сдвинуты по фазе, но на угол, меньший |
|||||||
|
|
1 |
1 |
|||||||||||
|
π |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 ); следовательно, мощность E1 I1 cosψ1 — положительна, так же |
|||||||
2 |
( I1 |
опережает |
E1 |
на угол ψ1 < |
|
|||||||||
как для вторичной обмотки трансформатора. Тем самым подтверждается, что при s<0 машина работает генератором.
Переходя от вращающейся машины, работающей генератором, к неподвижной машине, работающей трансформатором (рис. 3-34), мы должны иметь н.с. обмоток, равными по амплитуде F2 и F1 и сдвинутыми по фазе (во времени) так же, как они сдвинуты в пространстве при работе машины генератором.
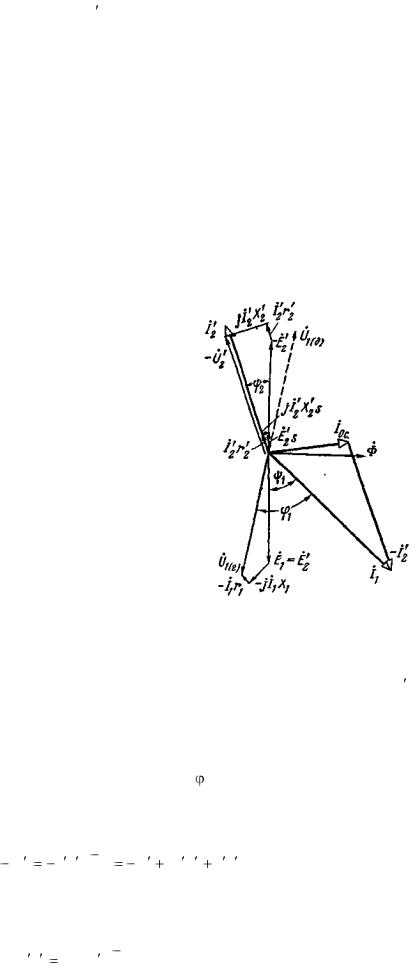
Следовательно, согласно уравнениям (3-98) векторная диаграмма трансформатора, эквивалентного асинхронному генератору, будет иметь вид, представленный на рис. 3-39 (здесь также показаны векторы э.д.с. и падений напряжения цепи вращающегося ротора при s < 0).
Рис. 3-39. Векторная диаграмма асинхронного генератора (приведенного к работе трансформатором).
При работе машины трансформатором с токами I1 и I2 , показанными на рис. 3-39, мы должны считать роторную обмотку за первичную, а статорную — за вторичную. На зажимах
вторичной обмотки мы будем иметь напряжение . Оно направлено против напряжения , которое было приложено к машине при ее работе двигателем. При этом мощность, отдаваемая
генератором в сеть, равна m1U1I1cos |
1. |
||||
Мы должны считать, что к зажимам первичной обмотки извне приложено.напряжение |
|||||
U2 |
I2r2 |
1 s |
E2 |
jI2 x2 |
I2r2 . |
|
|
|
|
|
|
s
Мощность, подводимая к первичной (роторной) обмотке, равна:
m U |
I |
|
m I 2r |
1 s |
. |
|||
2 |
|
|||||||
1 |
2 |
|
1 |
2 |
2 |
s |
||
|
|
|
|
|
|
|
||
Она является чисто активной мощностью и соответствует механической мощности ротора P2 при работе машины генератором со скольжением s.
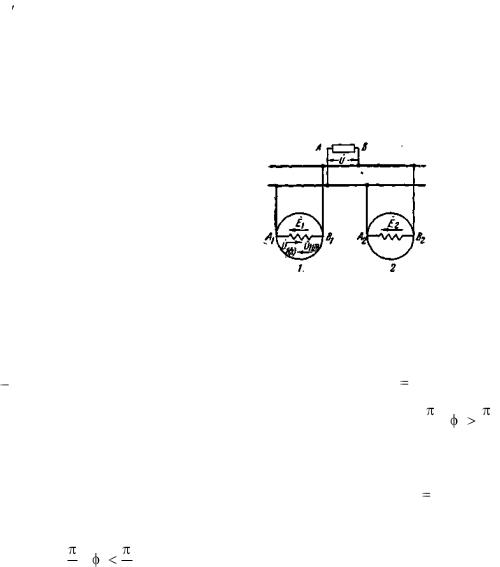
Для того чтобы выяснить, какие условности принимаются в отношении U1(г ) и U1(д) , обратимся к рис. 3-40. Будем считать, что машина 2 работает генератором с напряжением на его
зажимах U .
Рис. 3-40. К рассмотрению работы машины двигателем и генератором.
Если машина 1 работает двигателем и, следовательно, потребляет активную мощность, то
векторная |
диаграмма |
строится |
для обхода |
B2A2A1B1B2: |
|
для этого обхода величина |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
U |
1(д) , уравновешивающая э.д.с. |
ток |
|||||||||
|
E1 рассматривается как составляющая напряжения |
|
1 |
|
E1 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
относительно э.д.с. |
при этом сдвинут на угол, больший |
2 ( |
|
2 на рис. 3-35). |
|
|
|||||||||||||
I1 |
E1 |
|
|
|
|
||||||||||||||
|
Если |
машина |
1 |
работает |
генератором и, |
следовательно, |
|
отдает активную мощность, |
то |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторная диаграмма строится для обхода В1А1АBВ1; здесь |
U |
|
U |
|
|
|
|
|
|
||||||||||
|
|
|
|
1(г ) |
– составляющая э.д.с. E1 |
, равная |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
падению напряжения в сопротивлении А—В; при этом ток I1 относительно э.д.с. E1 сдвинут на угол,
меньший 2 ( 1 2 на рис. 3-39).
Реактивный ток, необходимый для возбуждения в асинхронной машине магнитного поля, она сама не может создавать. Он к ней должен подводиться из сети при всех режимах ее работы.
Асинхронный генератор может работать только при опережении током I1 э.д.с. E1 . Такой режим при одиночной работе генератора можно создать при помощи конденсаторов. Однако в обычных случаях требуются конденсаторы большой емкости. Они получаются громоздкими и дорогими: к тому же, если их емкость постоянна, то напряжение на зажимах генератора с увеличением нагрузки резко падает, а его стабилизация встречает большие затруднения.
Асинхронный генератор иногда включается на параллельную работу с синхронным генератором, позволяющим путем изменения его тока возбуждения изменять реактивную составляющую отдаваемого им тока (§ 4-7,в). Условия работы синхронной машины при этом ухудшаются, так как она должна работать с пониженным cos θc, отдавая отстающий реактивный ток не только во внешнюю сеть, но и асинхронной машине для создания в ней магнитного поля (рис. 3- 41).

Рис. 3-41. Диаграмма векторов напряжения U и токов: нагрузки I , асинхронного генератора Iас и
синхронного генератора Iс при их параллельной работе.
3-13. Вращающий момент
а) Зависимость момента от потока Ф и активной составляющей тока ротора I 2 cos ψ2 .
Вращающий момент в асинхронной машине, как отмечалось, создается в результате взаимодействия вращающегося поля и токов, наведенных им в обмотке ротора. Его значение можно найти, исходя из закона электромагнитных сил.
На рис. 3-42 представлены кривые распределения индукции В и наведенных в обмотке ротора токов i2по окружности ротора асинхронного двигателя, причем эти кривые приняты синусоидальными.
Рис. 3-42. Распределение индукции В, токов i2 и тангенциальных сил f по окружности ротора.

При постоянных напряжении на зажимах статора и нагрузке на валу двигателя (s = const) обе кривые имеют неизменные амплитуды Bм и I2м и остаются неподвижными одна относительно другой. Сдвиг между ними равен Ψ2 (в электрических радианах) в соответствии со сдвигом по фазе э.д.с. и тока ротора.
Электромагнитная сила, действующая в тангенциальном направлении на проводник с током,
f Bil . (3-107)
Возьмем проводник, сдвинутый на угол ξ (в электрических радианах) относительно нулевого значения индукции. Индукция в месте, где находится проводник, B = Bмsinξ; ток в этом проводнике
i2 I 2м sin(ξ ψ2 ) . Следовательно, |
|
f Bм I 2м l sin ξsin(ξ - ψ2 ) . |
(3-108) |
На рис. 3-42 (вверху) показана кривая распределения тангенциальных сил f на окружности ротора, найденная согласно (3-108). На этом же рисунке (внизу) показаны тангенциальные силы, приложенные к ротору.
Кривые В и i2 относительно статора вращаются с синхронной частотой ω1. С такой же частотой относительно статора вращается кривая f; относительно ротора она вращается с частотой sω1.
Среднее значение тангенциальных сил f, необходимое для расчета момента, определяется следующим образом:
f |
|
|
|
1 2π |
B |
I |
|
|
l sin ξsin(ξ - ψ |
|
)dξ |
|
1 |
|
B |
I |
|
|
|
l cosψ |
|
|
|
|
||||||||||||||
ср |
|
|
|
|
|
|
2м |
2 |
|
|
|
|
2м |
2 |
|
|
|
|||||||||||||||||||||
|
|
|
2π 0 |
м |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
м |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(3-109) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Общую силу F, действующую на ротор, найдем, умножив среднюю силу fср на число |
||||||||||||||||||||||||||||||||||||||
проводников N2 обмотки ротора: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
F |
fср N 2 . |
|
|
|
|
(3-110) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Вращающий момент равен произведению силы F на плечо 2 , где D'—диаметр ротора: |
||||||||||||||||||||||||||||||||||||||
M |
F |
D |
|
|
|
f |
|
|
N |
|
D |
1 |
B l |
|
|
lN |
|
D |
|
cosψ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
|
|
ср |
|
|
2 |
2 |
|
2 |
м |
2м |
|
2 |
2 |
|
|
|
|
|
|
(3-111) |
|
|
|||||||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
π |
|
πD |
|
|
|
η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Bм |
|
|
2 Bср |
; 2 p |
|
|
Bср lη |
|
|
; I 2м |
|
|
|
2I 2 , |
|
|
|
|
||||||||||||||||||||
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
получим, Дж:
M |
N |
2 p |
I |
|
cos ψ2 |
|
||
|
|
|
|
2 |
|
|||
2 |
2 |
|
|
|||||
|
|
|
|
. |
(3-112) |
|||
|
|
|
|
|
|
|
||

Формула (3-112) справедлива для обмотки ротора, выполненной в виде беличьей клетки. В общем случае для любой обмотки ротора необходимо учесть укорочение шага и распределение по окружности ротора катушек катушечной группы. Для этого нужно ввести в (3-112) обмоточный коэффициент k02, тогда момент, Дж,
M |
N |
2 pk02 |
I |
|
cos ψ 2 |
||
|
|
|
|
2 |
|||
2 |
2 |
|
|||||
|
|
|
|
(3-113) |
|||
|
|
|
|
|
|
|
|
или момент, кг.м,
M 0,102 |
N |
2 pk02 |
I |
|
cos ψ 2 |
|
||
|
|
|
|
2 |
|
|||
2 |
2 |
|
|
|||||
|
|
|
|
. |
(3-114) |
|||
|
|
|
|
|
|
|
||
Если помножить (3-113) на ω1, и при этом учесть, что
|
|
ω1 |
2πn1 |
|
2πf1 |
|
2π |
|
f1ω2 k |
|
E2 |
|
N 2 2m2 ω2 |
|
60 |
|
p |
|
|
|
|
02 |
|||
|
|
|
2 |
|||||||||
; |
|
|
; |
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|||
то получим выражение для электромагнитной мощности:
Pэм ω1M m2 E2 I2 cosψ2 m1E2 I2 cosψ2 .
Точно такое же выражение для Рэм мы получили при помощи векторной диаграммы двигателя (§ 3- 10).
Формула (3-113) показывает, что М зависит от величин Ф, I2 и cos ψ 2 , которые в свою очередь зависят от скольжения. Поэтому она не дает в явной форме зависимости М от скольжения или от частоты вращения. Однако вывод выражения (3-113) помогает уяснить физическую картину образования электромагнитного момента М.
б) Зависимость момента от скольжения.
Зависимость М = f(s) при исследовании рабочих свойств асинхронной машины имеет важное значение. При определении этой зависимости устанавливается также влияние на вращающий момент напряжения U1 на зажимах статора и параметров машины. Она может быть найдена из уравнений напряжений и токов (3-98) и уравнения мощностей (3-69), которые мы еще раз напишем в следующем виде:
U1 |
|
I0 c Z12 |
I1Z1 ; |
|
(3-115) |
|||||||
0 |
|
I 0c Z12 |
I 2 Z 2s ; |
|
(3-116) |
|||||||
I 2 |
I0c |
I1 ; |
|
|
|
(3-117) |
|
|
||||
|
|
P |
|
m |
2 |
I 2 r |
|
m I |
2 |
2 r |
|
|
M |
|
э2 |
|
|
2 |
2 |
|
1 |
2 |
|
||
|
sω1 |
|
|
sω1 |
|
sω1 |
, (3-118) |
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где (по аналогии с трансформатором) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I0с Z12 |
E1 |
|
|
E2 |
; |
|
(3-119) |
|||||

Z1 |
r1 |
|
|
|
|
|
|
|
jx1 ; |
|
|
|
|
|
(3-120) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Z2s |
|
r2 |
|
|
|
|
|
jx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
s |
|
|
|
|
|
|
. |
|
|
|
|
|
(3-121) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из (3-117) и (3-116) найдем: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
I0c |
I1 |
|
|
|
|
|
|
Z 2s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Z12 |
Z 2s . |
|
|
(3-122) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Подставляя найденное значение I0c |
в (3-115), получим: |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 Z 2s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
U1 |
I1 |
(Z1 |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 Z 2s . |
(3-123) |
|
|
|
|
|
||||||||||||||||
Из последнего равенства следует: |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z12 Z 2s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
I1 |
U1 |
|
|
Z1Z12 |
|
|
|
Z1Z 2s |
Z12 Z 2s . |
|
|
|
|
(3-124) |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Разделив числитель и знаменатель правой части на Z12, будем иметь: |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
Z 2s |
|
|
|
|
|
|
|
1 |
|
Z 2s |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
Z12 |
|
|
|
|
|
|
|
|
Z12 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
I1 |
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
U1 |
Z |
1 |
|
C Z |
2s |
|
|
||||||||
|
|
|
|
Z1 Z 2s |
|
|
|
|
|
|
|
Z 2s |
|
|
|
1 |
|
|
||||||||||||||||||
|
|
|
|
|
Z12 |
|
|
|
|
|
|
|
, |
(3-125) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
1 |
|
|
|
|
|
|
|
Z1 |
|
|
c e jγ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
Z12 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(3-126) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для нормальных асинхронных двигателей мощностью Рн > 1 2 кВт угол γ1 по абсолютной |
||||||||||||||||||||||||||||||||||||
величине обычно меньше 1° и имеет отрицательное значение; модуль с1 = 1,05 |
1,02. |
|||||||||||||||||||||||||||||||||||
Подставив в (3-116) значение |
I ос |
из (3-122) и затем в найденное равенство |
I |
|||||||||||||||||||||||||||||||||
|
|
|
1 из (3-125), |
|||||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I 2 |
|
U1 |
|
Z1 |
|
|
CZ 2 s . |
(3-127) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Учитывая равенства (3-120) и (3-121) и принимая С1 = c1, можем написать согласно (3-127) |
||||||||||||||||||||||||||||||||||||
формулу для модуля тока: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
I2 |
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(r c |
|
r2 |
)2 |
(x c x )2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
s |
|
|
1 1 2 |
|
|
. |
|
(3-128) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теперь можем найти искомую зависимость M = f(s), подставив в (3-118) полученное значение
I 2 :
|
|
m U 2 r |
|
|
|
|
||||
M |
|
|
1 |
1 |
2 |
|
|
|
|
|
sω [(r c |
r2 |
|
)2 |
|
(x |
c x |
)2 ] |
|
||
|
|
|
|
|||||||
|
|
|
|
|||||||
1 1 1 |
s |
|
|
|
1 |
1 2 |
. |
(3-129) |
||
В найденном уравнении параметры r1, x1, x2 и с1 приближенно считаются постоянными. Следовательно, М зависит только от s (при U1 = const). Отметим здесь также, что при данном s
момент пропорционален квадрату напряжения U12 .
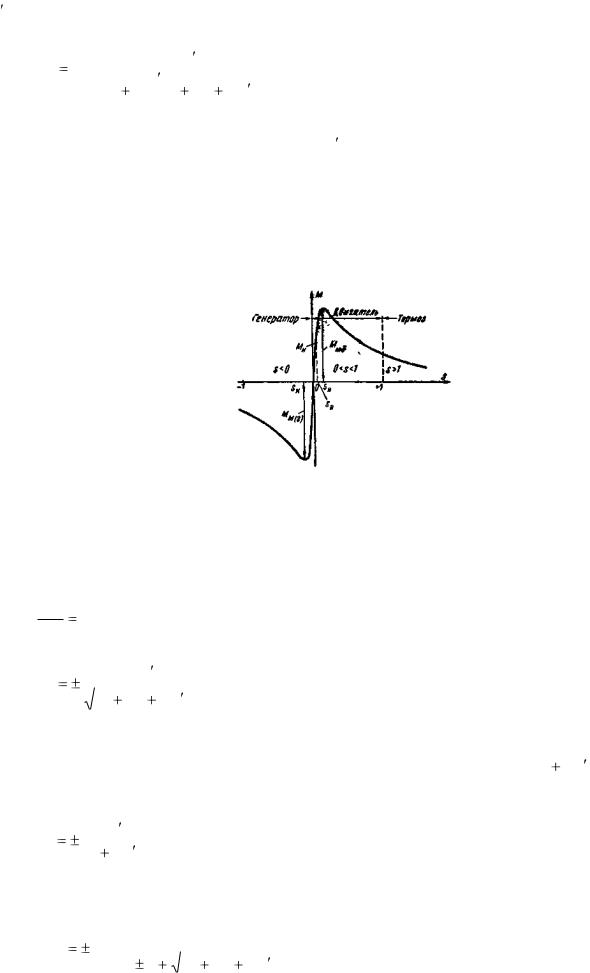
На рис. 3-43 представлена кривая M = f(s), построенная по уравнению (3-129). Она показывает, что вращающий момент имеет два максимума: один при s>0, другой при s<0.
Рис. 3-43. Кривая зависимости вращающего момента М от скольжения s трехфазной машины.
в) Максимальный момент.
Максимальный момент определяем обычным путем. Вначале найдем значение аргумента sk, при котором функция М будет максимальной. Для этого первую производную функции приравняем
dM |
0 |
|
нулю: ds |
||
. Отсюда получаем искомое значение |
sк |
|
|
|
c1r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r 2 |
|
(x |
|
c x )2 |
. |
(3-130) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
1 |
|
1 |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Скольжение sк — критическое скольжение, при котором момент достигает максимального |
|||||||||||||||||||||||
значения. В выражении (3-130) значение |
r 2 |
по сравнению со значением |
(x |
c x |
2 |
)2 |
|||||||||||||||||
1 |
1 |
1 |
мало и им |
||||||||||||||||||||
можно пренебречь. Это дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
sк |
|
|
c1r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
c1 x2 . |
|
|
|
|
(3-131) |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставив в (3-129) значение sк из (3-130), найдем максимальный вращающий момент: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m U 2 |
|
|
|
|
|
|
|
|
|
|
||||
M м |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2ω c [ r |
|
|
r 2 |
|
(x |
c x )2 ] |
. |
(3-132) |
|
|
|
|
||||||||||
|
|
|
|
1 |
1 |
|
1 |
|
|
|
1 |
1 |
1 |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Знак плюс в (3-130) 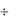 (3-132) относится к работе машины двигателем или тормозом, знак минус — к работе машины генератором.
(3-132) относится к работе машины двигателем или тормозом, знак минус — к работе машины генератором.
Так как r1 |
в нормальных двигателях мало по сравнению с |
x1 c1 x2 , то Мм зависит главным |
||||
образом от индуктивных сопротивлений рассеяния x1 и x2 . |
|
|||||
Для нормальных двигателей максимальный момент Мм |
больше номинального момента, |
|||||
соответствующего номинальной мощности на валу, в 1,8—2,5 раза: |
|
|||||
|
M м |
1,8 |
2,5 |
|
|
|
|
M н |
|
|
|||
|
|
. |
(3-133) |
|
||
|
|
|
|
|||
|
|
|
M м |
|
|
|
Значение |
M н |
определяет способность к перегрузке двигателя, причем здесь имеется в виду |
||||
перегрузка только в отношении вращающего момента, а не по нагреву.
Из (3-132) следует, что максимальный момент пропорционален квадрату напряжения, приложенного к статору. Поэтому понижение U1 приводит к заметному уменьшению Мм.
Так, например, если напряжение Ul понизилось по сравнению с номинальным U1н на 30%, то
|
|
|
|
|
M м |
2 |
|
M м при Ul = 0,7U1н будет составлять 0,72 = 0,49 от Мн при U1н; если отношение M н |
|||||||
, то теперь |
|||||||
|
M м |
0,49 |
2 |
0,98; |
|
|
|
|
M н |
|
|
||||
оно будет |
|
|
следовательно, двигатель не сможет нести даже |
номинальную |
|||
|
|
|
|||||
нагрузку на валу.
Еще больше ухудшаются условия, если обмотка статора ошибочно соединена звездой, а не треугольником, как это требуется при данном напряжении. Тогда напряжение, приложенное к фазе
обмотки, будет в |
3 раз меньше номинального, а максимальный момент, следовательно, |
уменьшится в 3 раза. |
|
Из (3-132) также следует, что значение Мм при данном напряжении не зависит от активного сопротивления r2 . От r2 согласно (3-130) зависит скольжение sк, при котором момент становится максимальным. На рис. 3-44 приведены кривые M = f(s) для различных значений r2 при работе
машины с s>0. Они показывают, что с увеличением r2 максимум момента смещается в сторону больших скольжений, сохраняя при этом свое значение. Аналогичные кривые получаются и для генераторного режима.
Рис. 3-44. Кривые M = /(s) для различных значений активного сопротивления r2 роторной цепи.
