
Асинхронные машины
.pdf
n2 (1 s)n1 . (3-72)
Номинальная частота вращения n2н, получающаяся при номинальной нагрузке на валу, указывается на щитке двигателя. Она в обычных случаях позволяет определить синхронную частоту вращения, число полюсов двигателя и его номинальное скольжение sн.
Например, на щитке двигателя, предназначенного для работы при частоте тока f1=50 Гц, указана частота вращения n2н = 730 об/мин. Ближайшая синхронная частота вращения равна 750 об/мин (табл. 3-3), чему соответствует число полюсов 2р = 8.
Скольжение
s% |
750 730 |
100% 2,67% |
|
|
750 |
. |
|||
|
|
При работе машины в обмотке ее ротора наводится э.д.с.
E2s |
4,44 f2 w2 k02 |
, |
(3-73) |
|
|
где w2 и k02 — число витков и обмоточный коэффициент обмотки ротора;
f |
|
(n1 n2 ) p |
|
n1 |
sf1 |
2 |
60 |
|
n1 |
||
|
|
|
(3-74) |
||
|
|
|
|
|
— частота э.д.с. и тока в обмотке ротора. С такой же частотой будет перемагничиваться сталь ротора. При работе машины двигателем частота f2 мала (при fi = 50 Гц f2 = 0,5  3-Гц), поэтому магнитными потерями в стали ротора можно пренебречь, что и было сделано при построении энергетической диаграммы на рис. 3-29.
3-Гц), поэтому магнитными потерями в стали ротора можно пренебречь, что и было сделано при построении энергетической диаграммы на рис. 3-29.
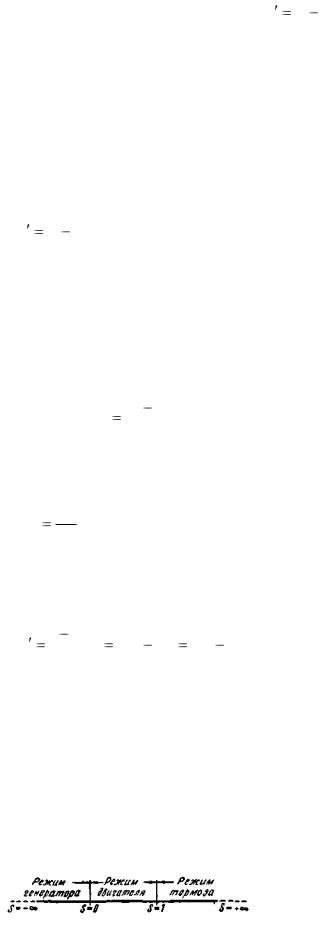
3-6. Режимы работы машин двигателем, тормозом и генератором
Асинхронная машина при изменении скольжения от 1 до 0 работает как двигатель. В этом случае электромагнитная мощность Pэм передается магнитным полем со статора ротору и частично
преобразуется в механическую мощность P2 (1 s)Pэм частично — в электрическую мощность Рэ2
= sРэм. При работе машины двигателем сдвиг между э.д.с. E1 , наведенной в фазе обмотки статора, и
током в этой фазе I1 больше 90°, так же как для первичной обмотки трансформатора.
Исходя из полученных ранее соотношений между мощностями асинхронной машины, можно
показать, что при изменении скольжения от s = l до s = ∞ машина работает как тормоз. Скольжение s>l получается при вращении ротора против поля. При этом электрические потери в цепи ротора Рэ2 = sРэм будут больше мощности Pэм и, следовательно, только частично покрываются за счет Рэм, передаваемой полем со статора ротору. Другая часть электрических потерь в цепи ротора (s-1)Рэм покрывается за счет механической мощности, приложенной к ротору. Механическая мощность
ротора P2 (1 s)Pэм будет отрицательной. Это значит, что она не отдается ротором, а подводится к нему и преобразуется в электрические потери в цепи ротора, т. е. поглощается в самой машине. Поэтому режим работы при s>l называется тормозным режимом.
Электромагнитный момент при этом действует на ротор в направлении вращения поля, т. е. против вращения ротора; следовательно, он является тормозящим по отношению к внешнему моменту, приложенному к валу машины.
Можно также показать, что при отрицательных скольжениях асинхронная машина работает
s |
n1 |
|
n2 |
|
|
n1 |
|
|
|
генератором. При |
|
|
< 0 ротор вращается в направлении вращения поля, но с частотой, |
|
|
|
|
||
превышающей частоту поля (n2 > n1). В этом случае электромагнитная мощность Рэм будет отрицательной, что следует из равенства
Pэм |
Pэ2 |
|
|
s . |
(3-75) |
||
|
Мощность Рэм при отрицательном скольжении передается полем с ротора статору. Механическая мощность Р'2 при этом будет также отрицательной, что следует из равенства
1 |
|
s |
|
Pэ2 |
|
|
|
P2 |
|
|
|
Pэ2 |
|
Pэ2 Pэм Pэ2 . |
|
|
s |
|
s |
(3-76) |
|||
Механическая мощность, следовательно, приложена к ротору. Часть ее идет на покрытие электрических потерь Рэ2 в цепи ротора, другая часть преобразуется в электромагнитную мощность
Рэм, передаваемую полем статору. При работе машины генератором сдвиг между E1 и I1 меньше 90° (§ 3-12), так же как для вторичной обмотки трансформатора.
На рис. 3-30 приведена шкала скольжений для режимов генератора, двигателя и тормоза. Указанные режимы работы асинхронной машины и их использование для практических целей более подробно будут рассмотрены в последующем.
Рис. 3-30. Шкала скольжений для режимов генератора, двигателя и тормоза.
3-7. Аналогия с трансформатором
Между обмотками статора и ротора асинхронной машины, как отмечалось, существует только магнитная связь; здесь энергия из одной обмотки в другую передается через посредством магнитного поля.
В последующем будет показано, что при любом скольжении машины н.с. обмоток статора и ротора вращаются относительно статора с одной и той же частотой и, следовательно, неподвижны одна относительно другой. Поле в машине создается их совместным действием.
Примем, так же как для трансформатора, что в асинхронной машине при ее работе имеют место основное поле и поле рассеяния. Индукционные линии основного поля проходят через воздушные зазоры, зубцы и ярма статора и ротора и сцепляются с обеими обмотками — статорной и роторной. Этому полю соответствует главный поток Ф в воздушном зазоре.
Индукционные линии полей рассеяния проходят между стенками пазов, вокруг лобовых частей обмоток и между коронками зубцов (§ 3-16). Так как магнитные сопротивления для потоков индукционных трубок рассеяния определяются в основном воздушными промежутками, то в первом приближении их можно принять постоянными и в соответствии с этим считать постоянными индуктивности рассеяния обмоток статора и ротора Lζ1 и Lζ2 (как для первичной и вторичной обмоток трансформатора).
Главный поток Ф наводит в обмотке статора э.д.с.
E1 |
4,44 f1w1k01 |
(3-77) |
|
|
и в обмотке ротора, вращающегося относительно поля со скольжением s, э.д.с.
E2s |
4,44 f2 w2 k02 |
. |
(3-78) |
|
|
Так как согласно (3-74) f2 = sf1, то можно написать:
E2s 4,44sf1w2 k02 |
sE2 , |
(3-79) |
где
E2 |
4,44 f1w2 k02 |
(3-80) |
|
|
есть э.д.с., наведенная в обмотке ротора при s = l, т. е. при неподвижном роторе.
Поля рассеяния наводят в обмотках статора и ротора э.д.с. рассеяния Eζ1 и Eζ2s , которые можно считать пропорциональными соответствующим токам:
Eζ1 |
jI1 x1 |
; |
Eζ 2s |
jI 2 x2s . |
(3-81) |
|
|
|
|
|
|
Индуктивное сопротивление рассеяния статорной обмотки
x1 2πf1Lζ1 . (3-82)
Индуктивное сопротивление рассеяния роторной обмотки

x2s 2πf2 Lζ2 2πsf1Lζ2 sx2 , |
(3-83) |
где x2 = 2πf1Lζ2 — сопротивление при неподвижном роторе (при s = l).
Наряду с индуктивными сопротивлениями рассеяния обмотки статора и ротора имеют активные сопротивления r1 и r2.
Таким образом, допустив, что в машине существуют основное поле (и соответствующий ему поток Ф) и отдельно поля рассеяния, мы можем для обмотки статора, так же как для первичной обмотки трансформатора, написать уравнение напряжений
U1 |
E1 |
jI1 x1 |
I1r1 . |
(3-84) |
|
|
|
|
|
Для обмотки ротора уравнение напряжений напишется в следующем виде:
0 E2s |
jI 2 x2 |
I 2 r2 |
sE2 |
jI 2 sx2 |
I 2 r2 . |
(3-85) |
|
|
|
|
|
|
|
В дальнейшем мы покажем, что при составлении соотношений, устанавливающих связь между напряжением, токами, мощностями, вращающим моментом и скольжением асинхронной машины, а также связи этих величин с ее параметрами, можно исходить из ее аналогии с трансформатором; при этом вращающаяся асинхронная машина заменяется неподвижной,
r2
работающей как трансформатор с активным сопротивлением роторной цепи s и ее индуктивным сопротивлением рассеяния х2.
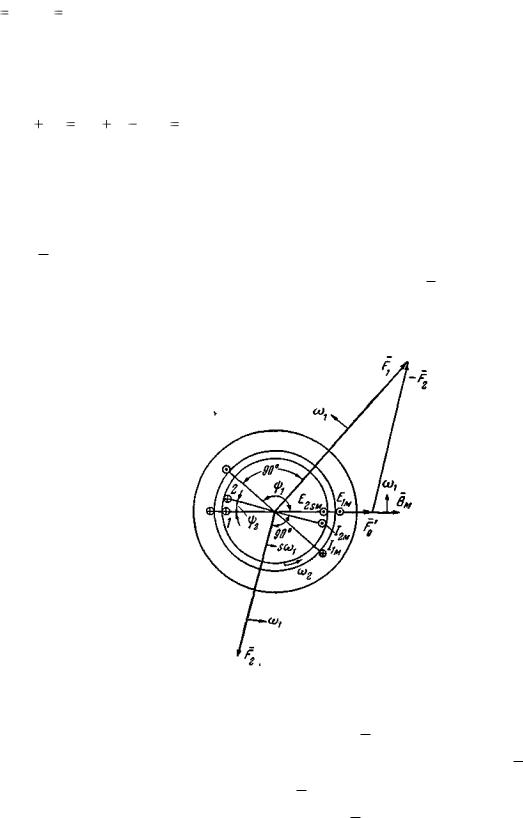
3-8. Пространственная диаграмма н.с. двигателя
Как указывалось, основное поле в машине создается совместным действием н.с. обмоток статора и ротора.
Намагничивающая сила обмотки статора вращается относительно статора с частотой n1 (об/мин) (или с угловой частотой ω1).
|
Намагничивающая сила обмотки ротора вращается относительно ротора с частотой |
||
60 f1 |
|
60sf1 |
sn1 |
p |
|
p |
|
|
(или sω1) в направлении его вращения. Последнее объясняется тем, что при одном |
||
|
|
|
|
и том же направлении вращения поля относительно обмоток статора и ротора (при s>0) порядки чередования фаз этих обмоток будут одинаковы. Так как сам ротор вращается в сторону вращения поля с частотой n2(ω2), то н. с. ротора относительно статора вращается с частотой
sn1 n2 sn1 (1 s)n1 n1 (ω1 ) .
Отсюда видим, что н.с. статора и ротора вращаются относительно статора в одну и ту же сторону с одной и той же частотой; следовательно, они неподвижны одна относительно другой.
Обратимся к рис. 3-31, где изображены статор и ротор вращающейся машины. Ее основное поле, синусоидально распределенное в воздушном зазоре, можно изобразить пространственным
вектором Bм , вращающимся с синхронной частотой ω1. При этом индукция в любой точке
внутренней окружности статора определяется проекцией вектора Bм на линию, проведенную через центр и выбранную точку.
Рис. 3-31. Пространственная диаграмма н.с. двигателя (sω1 + ω2 = ω1).
Пусть в рассматриваемый момент времени вектор Bм направлен по горизонтали, как показано на рис. 3-31. Такое же направление будет иметь пространственный вектор F0 н.с. создающей в воздушном зазоре основное поле с амплитудой Bм . В этот момент времени в фазах обмоток статора и ротора, оси которых перпендикулярны к вектору Bм , будут наводиться максимальные э.д.с.
н.с. создающей в воздушном зазоре основное поле с амплитудой Bм . В этот момент времени в фазах обмоток статора и ротора, оси которых перпендикулярны к вектору Bм , будут наводиться максимальные э.д.с.
E1м и E2sм . Направления E1м и E2sм , найденные по правилу правой руки, одинаковы при s>0, так как в этом случае поле относительно обеих обмоток перемещается в одну и ту же сторону (против часовой стрелки).
Если бы роторная цепь имела только активное сопротивление, то максимум тока I2м в фазе обмотки ротора получался бы одновременно с максимумом э.д.с. E2sм в этой фазе. Но так как роторная цепь наряду с активным сопротивлением имеет индуктивное сопротивление рассеяния, то максимум тока I2м наступит позднее, чем максимум э.д.с. E2sм. В рассматриваемый момент времени максимальный ток I2м будет иметь место в фазе 2, сдвинутой относительно фазы 1 на угол ψ2 (в электрических радианах) в соответствии со сдвигом по фазе (во времени) на угол ψ2 э.д.с. и тока в обмотке ротора.
Так как амплитуда вращающейся н.с. совпадает с осью той фазы, ток которой имеет в данный
момент времени максимальное значение (рис. 3-27), то пространственный вектор F2 н.с. роторной обмотки совпадает с осью фазы 2.
Результирующая н.с. F0 F1 F2 . Следовательно, F1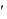 F0 F2 . Последнее равенство при известных F0
F0 F2 . Последнее равенство при известных F0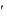 и F2 позволяет определить пространственный вектор F1 н.с. статора и ту фазу его обмотки, которая имеет максимальный ток I1м .
и F2 позволяет определить пространственный вектор F1 н.с. статора и ту фазу его обмотки, которая имеет максимальный ток I1м .
На рис. 3-31 показаны векторы н.с. и только те фазы обмоток статора и ротора, в которых э.д.с. и токи в рассматриваемый момент времени имеют максимальные значения.
Значения Bм и соответствующего потока Ф, сцепляющегося с обмоткой статора, определяются в основном напряжением U1: поток Ф должен иметь такое значение, чтобы наведенная им э.д.с. E1 почти полностью уравновешивала напряжение U1. При увеличении скольжения, что вызывается возрастанием нагрузки на валу, увеличиваются ток I2 и F2, а это в свою очередь
приводит к увеличению I1 и F1, так как н.с. F0 должна остаться почти неизменной, поскольку остается почти неизменным создаваемый ею поток Ф.
3-9. Приведение вращающейся машины к неподвижной, работающей как трансформатор
Намагничивающая сила ротора при его вращении совместно с н.с. статора создает основное толе. Очевидно, что точно такое же поле будет создаваться в машине и при неподвижном роторе, если токи в его обмотке по величине и фазе (относительно э.д.с.) остаются теми же, что и при вращении.
На рис. 3-32 представлена векторная диаграмма роторной цепи при s>0, соответствующая уравнению напряжений (3-85).
Рис. 3-32. Векторная диаграмма роторной цепи при s > 0.
Из этого уравнения находим:
I |
|
|
E2s |
|
|
|
|
|
2 |
|
|
|
|
|
|
||
r 2 |
x2 |
(3-86) |
||||||
|
|
|
||||||
|
|
|
2 |
2s . |
||||
Если числитель и знаменатель правой части равенства разделить на s, то получим тот же ток
I2 |
|
|
|
E2 |
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
r2 |
|
|
|
|
|
|
|
x2 |
|
|||
|
|
|
|
|
|||
|
|
|
s |
2 |
|
|
|
|
|
|
, |
(3-87) |
|||
|
|
|
|
||||
где Е2 и х2 — э.д.с. и индуктивное сопротивление рассеяния роторной цепи при неподвижном роторе.
Таким образом, вместо вращающегося ротора можно рассматривать неподвижный ротор, но r2
при этом необходимо считать активное сопротивление его цепи равным s . В этом случае ток роторной цепи I2 остается тем же самым, что и при скольжении s, так же как и сдвиг его по фазе ψ2 относительно э.д.с. (рис. 3-32 и 3-33).
Рис. 3-33. Векторная диаграмма роторной цепи при неподвижном роторе.
Теперь мы можем перейти от вращающегося ротора к неподвижному (эквивалентному), взяв здесь только фазы статора и ротора, оси которых совпадают, и рассматривать работу машины как работу условного трансформатора, первичная (статорная) и вторичная (роторная) обмотки которого пронизываются одновременно одним и тем же главным потоком Ф (рис. 3-34). При этом необходимо, чтобы н.с. обмоток по амплитуде были равны F1 и F2 и чтобы эти н.с. по фазе (во времени) были сдвинуты на такой же угол, на который они были сдвинуты в пространстве при работе машины двигателем.
Уравнения напряжений для фаз статора и ротора можем написать так же, как для первичной и вторичной обмоток трансформатора. Уравнение напряжений роторной цепи (3-85) после деления его членов на s получает следующий вид:
|
|
|
r2 |
|
|
0 F2 |
jI 2 x2 |
I 2 |
s . |
(3-88) |
|
Отсюда также видим, что при замене вращающейся машины неподвижной, когда она работает как трансформатор (рис. 3-34), нужно в ее роторной цепи иметь активное сопротивление r2
s .

Рис. 3-34. Фазы обмоток статора и ротора асинхронной машины, работающей как трансформатор.
Тогда временной сдвиг н.с. статорной и роторной обмоток такого трансформатора будет соответствовать пространственному сдвигу н.с. вращающейся машины и мы можем написать:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F1 |
F2 |
|
|
|
F0c |
; |
|
(3-89) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
здесь |
F0c |
взято с учетом потерь в стали статора Pс1, и вследствие этого несколько отличается от |
|||||||||||||||||||||||
F0 на диаграмме рис. 3-31, где для упрощения мы пренебрегали этими потерями (практически |
|||||||||||||||||||||||||
F0c |
F0 ). Согласно (3-59) перепишем уравнение (3-89) в следующем виде: |
||||||||||||||||||||||||
|
|
|
|
|
w1k |
01 |
|
|
|
|
|
w2 k02 |
|
|
w1k |
01 |
|
|
|||||||
|
0,45m |
1 |
I |
1 |
|
|
|
|
|
0,45m |
2 |
I |
2 |
|
0,45m I |
0c |
|
|
|
|
|
||||
|
|
|
|
|
|
p |
|
|
|
|
|
p |
1 |
|
p |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(3-90) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,45m1 |
w1k01 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|||||
|
Разделим обе части этого равенства на |
|
|
|
|
. При этом получим: |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
I1 |
I 2 |
|
|
I0c , |
|
|
(3-91) |
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 2 |
I 2 |
|
m2 |
|
w2 k02 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
m |
|
w k |
|
|
|
(3-92) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
01 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
есть ток ротора, приведенный к обмотке статора.
w1k01
Обратимся теперь к уравнению напряжений роторной цепи (3-88). Помножим его на w2 k02 и
m1 w1k01 m2 w2 k02
два последних члена правой части еще на m2 w2 k02 m1 w1k01 .
Тогда, учитывая формулы для э.д.с. (3-77) и (3-80) и для приведенного тока (3-92), получим:
|
|
|
r2 |
|
|
0 F2 |
jI 2 x2 |
I 2 |
s , |
(3-93) |
|
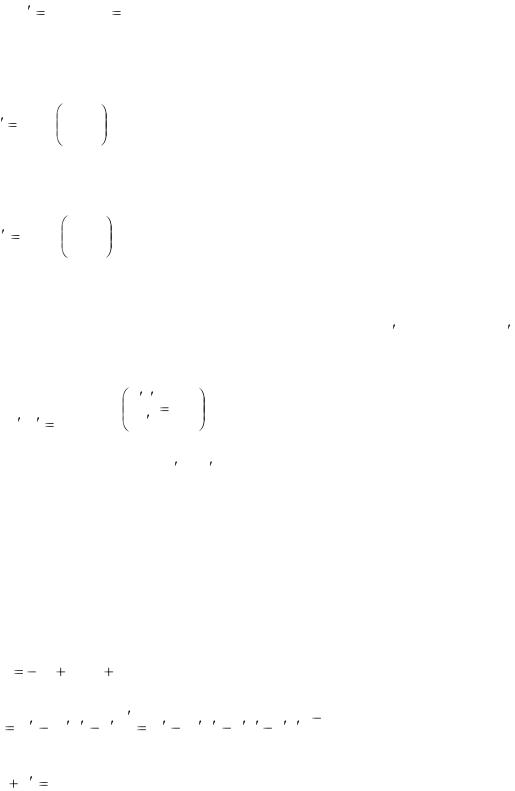
|
|
w1k01 |
|
|
F2 |
E2 |
w k |
|
E1 |
где |
2 |
02 |
(3-94) |
|
|
|
|||
— э.д.с. обмотки ротора, приведенная к обмотке статора;
|
|
m1 |
w1k01 |
2 |
|||||||
r2 |
r2 |
|
|||||||||
m |
|
|
w k |
|
|
|
(3-95) |
||||
|
2 |
|
|
2 |
02 |
|
|||||
|
|
|
|
|
|||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
w1k01 |
2 |
|||||
x2 |
x2 |
|
|
||||||||
m |
|
|
w k |
|
|
(3-96) |
|||||
|
2 |
|
2 |
|
02 |
||||||
|
|
|
|
||||||||
—сопротивления обмотки ротора, приведенные к обмотке статора.
Сучетом (3-92) и (3-94) те же соотношения между r2 и r2 и между х2 и x2 мы получили бы, исходя из равенств:
|
|
|
|
|
|
I2r2 |
|
I2r2 |
|
|
m I |
2 |
2 r m |
I 2 r |
и |
E2 |
|
E2 |
; |
(3-97) |
|
1 |
2 |
2 |
2 2 |
|
|
|
||||
Приведенные величины E2 и I 2 |
были бы равны действительным величинам обмотки ротора, |
|||||||||
если бы она была выполнена с теми же числами фаз, витков в фазе, пазов на полюс и фазу и с тем же шагом, что и обмотка статора. В такой обмотке электрические потери, а также относительные падения напряжения согласно (3-97) должны остаться неизменными.
3-10. Векторная диаграмма асинхронного двигателя
На основе уравнений напряжений (3-84) и (3-93) и уравнения токов (3-91), которые мы еще раз напишем:
U1 |
|
E1 |
jI1 x1 |
|
I1r1 |
; |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
r2 |
|
|
|
|
|
1 |
s |
||||
0 E2 |
jI |
2 x2 |
I |
|
|
|
E2 |
jI 2 x2 |
I 2 r2 |
I 2 r2 |
|
|
|
|
|
2 s |
|
s |
; |
||||||||||||
I1 |
I 2 |
I0c , |
|
(3-98) |
|
|
|
|
|
|
|
||||
могут быть построены векторные диаграммы асинхронной машины, приведенной к работе трансформатором.
На рис. 3-35 представлена диаграмма, соответствующая работе машины двигателем.
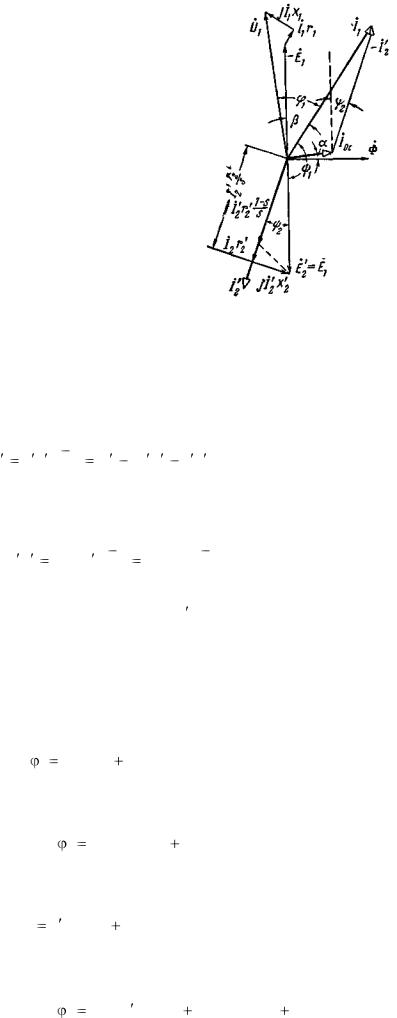
Рис. 3-35. Векторная диаграмма асинхронного двигателя (приведенного к работе трансформатором).
Она аналогична векторной диаграмме трансформатора, имеющего чисто активную нагрузку.
К первичной (статорной) обмотке подведено напряжение U1 . На зажимах, приведенной вторичной (роторной) обмотки, получается напряжение
U |
2 |
I 2 r2 |
s |
E2 |
jI 2 x2 |
I 2 r2 . |
(3-99) |
|
|
|
1 s |
|
|
|
|
Мощность, отдаваемая вторичной обмоткой, равна:
m U |
I |
|
m I 2 r |
1 s |
m |
I 2 r |
1 s |
|
|||||
2 |
|
|
|
|
|||||||||
1 |
2 |
|
1 |
2 |
2 |
s |
2 |
2 |
2 |
s , |
(3-100) |
||
|
|
|
|
|
|
|
|
|
|
||||
т. е. той механической мощности P2 , которую развивал бы ротор машины при работе ее двигателем со скольжением s [cм. уравнение (3-70а)].
Из диаграммы на рис. 3-35 мы можем также получить выражение для электромагнитной мощности Рэм, передаваемой полем со статора ротору. Для этого спроектируем векторы напряжений
обмотки статора на направление вектора I1 . Будем иметь:
U1 cos |
1 |
E1 cosβ |
I1r1 . |
|
|
(3-101) |
|
|
|
|
|||||||
Умножим полученное уравнение на m1I1; |
|
|
|
||||||||||||||
m U |
I |
1 |
cos |
1 |
m E I |
1 |
cosβ |
|
|
m I 2 r |
|
(3-102) |
|
|
|
||
1 1 |
|
|
1 |
1 |
|
|
|
|
1 1 1 . |
|
|
|
|
||||
Из диаграммы следует, что |
|
|
|
|
|
|
|
|
|||||||||
I1 cosβ |
I2 |
cosψ2 |
I0c |
sin α |
. |
(3-103) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя (3-103) в (3-102), получим: |
|
|
|
||||||||||||||
m U |
I |
|
cos |
|
m E I |
|
cosψ |
|
|
m E I |
|
sin α m I |
2 r |
, |
(3-104) |
||
1 1 |
|
1 |
|
1 |
1 |
1 |
2 |
|
|
2 |
1 1 |
0c |
1 1 1 |
||||
