
Асинхронные машины
.pdf
Равенство (3-40) согласно известному уравнению
2sin |
1 |
(α |
β) cos |
1 |
(α β) sinα sinβ |
|
2 |
2 |
|||||
|
|
|
|
может быть записано в следующем виде:
F |
|
1 |
F |
|
sin |
ωt |
|
xπ |
|
1 |
F |
sin ωt |
xπ |
. |
|
||
2 |
|
|
η |
2 |
|
|
|||||||||||
tx1 |
мq1 |
|
|
|
мq1 |
|
η |
(3-41) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первое слагаемое правой части обозначим через F': |
|||||||||||||||||
F |
1 |
F |
sin |
ωt |
xπ |
, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
мq1 |
|
|
|
|
η |
|
|
(3-42) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полученное уравнение называется уравнением бегущей волны. Оно показывает, что н.с. F  является функцией времени t и места х. Если принять, что выражение в скобках равняется постоянной величине с (изменение t компенсируется изменением х), то мы найдем, с какой частотой
является функцией времени t и места х. Если принять, что выражение в скобках равняется постоянной величине с (изменение t компенсируется изменением х), то мы найдем, с какой частотой
|
|
|
|
|
|
|
|
|
|
|
|
ωt |
xπ |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
η |
||
будет перемещаться н.с. |
Действительно, дифференцируя уравнение |
по t, |
||||||||||||
|
ω |
|
π |
|
dx |
0, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
η |
|
dt |
|
|
|
|||||||
получим: |
|
|
|
|
а отсюда |
|
|
|||||||
v1 |
|
dx |
|
|
|
ωη |
|
2πf1η |
|
2ηf1. |
|
|
||
|
dt |
|
|
π |
|
π |
|
|
||||||
|
|
|
|
|
(3-43) |
|
|
|||||||
С такой частотой будет перемещаться любое значение н.с., а следовательно, и ее амплитуда
1 |
F |
. |
|
||
2 |
мq1 |
Так как при вращательном движении перемещение на 2 соответствует |
частота вращения волны н.с. (ее первой гармоники),об/с,
n1 |
f1 |
|
p |
||
|
и ─ в об/мин,
1
p части оборота, то
n1 |
60 f1 |
|
|
|
p |
. |
(3-44) |
||
|
||||
|
|
Обозначив второе слагаемое равенства (3-41) через F", мы также получим уравнение бегущей
волны:
F |
1 |
F |
sin(ωt |
xπ |
) |
|
|
|
|
||||
|
2 |
мq1 |
|
η . |
(3-45) |
|
|
|
|
||||
Однако частота ее перемещения и v1 , найденная аналогичным образом, будет отрицательной:
dx |
|
|
v1 dt |
2ηf1 , |
(3-46). |
так же как и частота вращения, об/мин,
n1 |
60 f1 |
|
|
|
p |
. |
(3-47) |
||
|
||||
|
|
Это значит, что н.с. F перемещается в обратную сторону (положительному приращению dt соответствует отрицательное приращение dx).
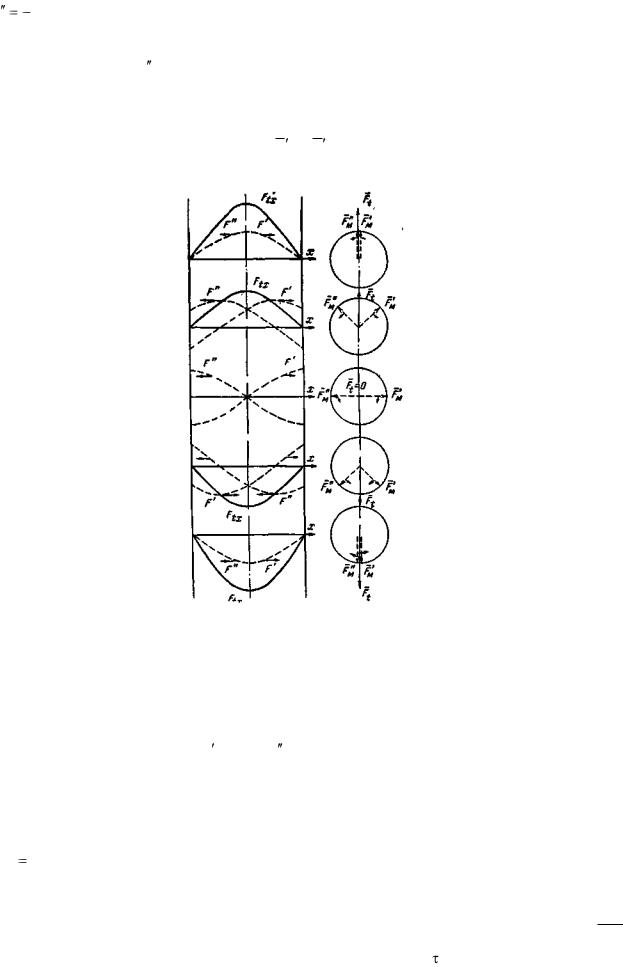
Таким образом, мы получили две вращающиеся н.с., которые можно изобразить вращающимися пространственными векторами Fм и Fм (рис. 3-26).
(рис. 3-26).
Рис. 3-26. Замена пульсирующей н.с. двумя круговыми вращающимися н.с.
Пространственным вектором заменяется синусоидально распределенная н.с. Его проекция на линию, проведенную через центр внутренней окружности статора и любую ее точку, определяет н.с., соответствующую этой точке.
|
|
|
|
|
|
||||
Пространственный вектор |
Fм или Fм при вращении опишет окружность, поэтому |
||||||||
соответствующая н.с. называется круговой вращающейся н.с. |
|||||||||
Определим значение ν -й гармоники н.с. для той же точки х (рис. 3-25). Оно равно: |
|||||||||
F |
F |
sin ωt cos |
νxπ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
txν |
мqν |
|
η , |
(3-48) |
|
|
|||
|
|
|
|
|
|||||
νxπ
так как теперь тому же сдвигу х относительно оси фазы А будет соответствовать сдвиг η в электрических радианах (полюсное деление для ν -й гармоники равно /ν). Заменим пульсирующую н.с. Ftxν двумя вращающимися:
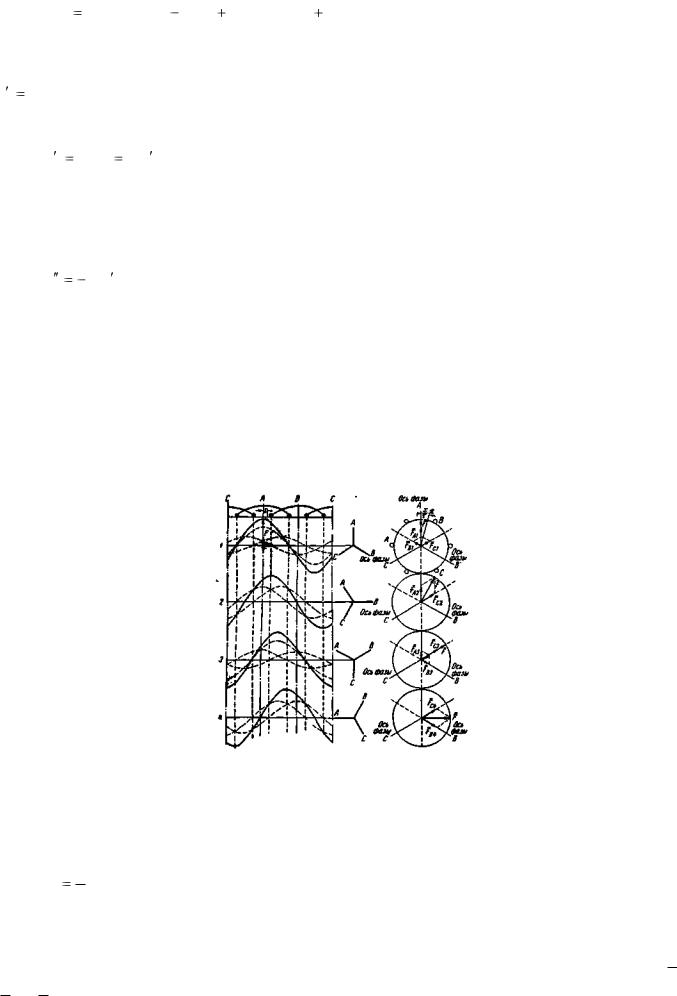
F |
1 |
F |
sin(ωt |
νxπ |
) |
1 |
F |
sin(ωt |
νxπ |
) |
|
|
|
|
|
|
|||||||
txν |
2 |
мqν |
|
η |
2 |
мqν |
|
η . |
(3-49) |
||
|
|
|
|
|
|||||||
Рассуждая аналогично предыдущему, найдем, что одна из них перемещается со скоростью
vν |
2 |
η |
f1 |
|
|
|
|
|
|
|
ν |
или вращается с частотой |
|||||||||
|
|
|
||||||||
|
|
nν |
|
60 f1 |
1 |
n1 |
|
|||
|
|
|
νp |
|
ν |
(3-50) |
||||
|
|
|
|
|
|
, |
||||
в ν раз меньшей частотой вращения первой гармоники. Вторая н.с. вращается в обратную сторону с той же частотой:
n |
|
1 |
n |
|
|
|
|
||
|
ν |
ν 1 . |
(3-51) |
|
б) Многофазная обмотка.
Вначале найдем н.с. трехфазной обмотки. Она может быть найдена графически, путем сложения н.с. отдельных фаз с учетом пространственного сдвига осей фаз и сдвига во времени их токов.
На рис. 3-27 слева показано сложение первых гармоник н.с. фаз трехфазной обмотки для отдельных моментов времени.
Рис. 3-27. Намагничивающая сила трехфазной обмотки.
В результате сложения получается синусоидально распределенная н.с. с неизменной амплитудой, в 1,5 раза большей максимальной амплитуды н.с. фазы:
3
F 2 Fмq1 . (3-52)
К тому же результату можно прийти, рассматривая синусоидально распределенную н.с. каждой фазы как пространственный вектор, выходящий из центра внутренней окружности статора и
совпадающий с осью данной фазы. Пространственные векторы пульсирующих н.с. фаз обмотки FAn ,
FBn , FCn (n=l, 2, 3, 4) показаны на рис. 3-27 справа. Их мгновенные значения и направления

соответствуют мгновенным значениям и направлениям токов в фазах обмотки. Складывая векторы
н.с. FAn , FBn , FCn для отдельных моментов времени, получим результирующий пространственный вектор F , неизменный по величине, но вращающийся в определенном направлении.
Мы видим, что вектор результирующей н.с. вращается в направлении от A к В и к С. При этом амплитуда н.с. совпадает с осью той фазы, ток которой в данный момент времени имеет максимальное значение. Положительные максимальные значения токов в фазах устанавливаются сначала в фазе А, затем в фазе В и, наконец, в фазе С. Этим определяются порядок чередования фаз и направление вращения амплитуды результирующей н.с.
Изменив порядок чередования фаз путем перемены мест двух проводов, подводящих ток к обмотке статора асинхронного двигателя, мы изменим направление вращения н.с. и создаваемого ею поля, а следовательно, направление, вращения ротора двигателя.
Из рис. 3-27 видно, что за четверть периода изменения тока результирующая н.с. пройдет 0,5 , а за период — 2 . Следовательно, ее линейная скорость перемещения v1 = 2 f1, а частота вращения, об/мин,
n1 |
60 f1 |
|
|
|
p |
. |
(3-53) |
||
|
||||
|
|
То же самое в общем виде можно доказать, обращаясь к аналитическим выражениям н.с. отдельных фаз. Для этого найдем н.с. фаз A, В, С в точке, сдвинутой на х относительно оси фазы А (рис. 3-27). Фаза А создает в этой точке н.с.
|
|
|
F |
|
F |
|
sin ωt cos |
xπ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Atx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
мq1 |
|
|
η |
, |
|
(3-54) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Так как токи в фазах В и С относительно тока в фазе А сдвинуты по фазе (во времени) на углы |
||||||||||||||||||
|
2π |
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
4π |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 и |
3 рад, а оси фаз В к С относительно оси фазы А сдвинуты на 3 и |
3 эл. рад., то н.с. фаз В и |
||||||||||||||||||
С в тот же момент времени в рассматриваемой точке равны: |
|
|
|||||||||||||||||||
|
|
|
F |
|
F |
sin ωt |
2π |
cos |
xπ |
|
2π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Btx |
мq1 |
|
|
3 |
|
|
η |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
; |
(3-55) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F |
|
F |
sin ωt |
4π |
cos |
xπ |
|
4π |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ctx |
мq1 |
|
|
3 |
|
|
η |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
. |
(3-56) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если сложить найденные значения н.с., заменив при этом каждую пульсирующую н.с. двумя вращающимися в разные стороны (3-41):

F |
F |
|
sin ωt cos |
2π 1 |
F |
|
|
sin ωt |
|
xπ |
1 |
F |
sin ωt |
xπ |
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Atx |
|
мq1 |
|
|
|
|
3 |
2 |
|
|
мq1 |
|
|
|
|
|
η |
2 |
мq1 |
|
η |
|
|||||||||||
F |
F |
|
sin ωt |
|
2π |
|
|
cos |
|
xπ |
|
2π |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Btx |
|
мq1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
η |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
F |
sin |
ωt |
|
|
xπ |
1 |
|
F |
|
sin |
ωt |
xπ |
4π |
; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
мq1 |
|
|
|
|
|
|
η |
2 |
|
|
|
мq1 |
|
|
|
|
η |
3 |
|
|
|
|
||||||||
F |
F |
|
sin ωt |
|
4π |
|
|
cos |
|
xπ |
|
4π |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ctx |
|
мq1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
η |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
F |
sin |
ωt |
|
|
xπ |
1 |
|
F |
|
sin |
ωt |
xπ |
2π |
, |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
мq1 |
|
|
|
|
|
|
η |
2 |
|
|
|
мq1 |
|
|
|
|
η |
3 |
|
|
|
(3-57) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то получим результирующую н.с.
F |
F |
F |
F |
3 |
F |
sin ωt |
|
xπ |
|
|
|
|
|
||||
2 |
|
|
η |
|
|
|
|
||||||||||
tx |
Atx |
Btx |
Ctx |
мq1 |
|
|
|
|
|
, |
(3-58) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где сумма вторых слагаемых (3-57) |
равна нулю, так как они представляют собой синусоиды с |
||||||||||||||||
|
|
|
|
|
|
|
|
4π |
|
|
2π |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
равными амплитудами, сдвинутые на |
3 |
|
и 3 рад. |
|
|
|
|||||||||||
Уравнение (3-58) — уравнение бегущей волны, перемещающейся с частотой v1 = 2 f1 или |
|||||||||||||||||
|
|
|
n1 |
|
60 f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
вращающейся с частотой |
|
|
[ср. с (3-42) и (3-44)]. |
|
|
||||||||||||
|
|
|
|
|
|||||||||||||
Таким образом, мы доказали, что результирующая н.с. трехфазной обмотки при наличии в |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
3 |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ней трехфазного тока является н.с. с неизменной амплитудой |
2 мq1 , вращающейся с частотой |
||||||||||||||||
n1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если стальные участки магнитной цепи ненасыщены, то кривая н.с. в другом масштабе дает нам кривую поля машины, которая, так же как и кривая н.с., вращается при неизменной амплитуде с частотой п1. Такое поле называется круговым вращающимся полем.
В общем случае симметричная m-фазная обмотка при наличии в ней симметричного m- фазного тока создает вращающуюся н.с. с постоянной амплитудой
F |
m |
Fмq1 |
0,45mI |
wk |
0 |
|
|
|
2 |
p |
, |
(3-59) |
|||||
|
|
|
||||||
которую аналогично предыдущему можно найти графически или аналитически путем сложения н.с. отдельных фаз.
Уравнения (3-58) и (3-59) получены для первых гармоник н.с. Они и используются в общей теории машин при определении их рабочих свойств, высшими гармониками при этом пренебрегают, так как амплитуды их незначительны.
Однако для более подробного изучения свойств машин необходимо выяснить, от чего зависят амплитуды высших гармоник н.с. обмоток и с какой частотой они вращаются относительно статора или ротора.
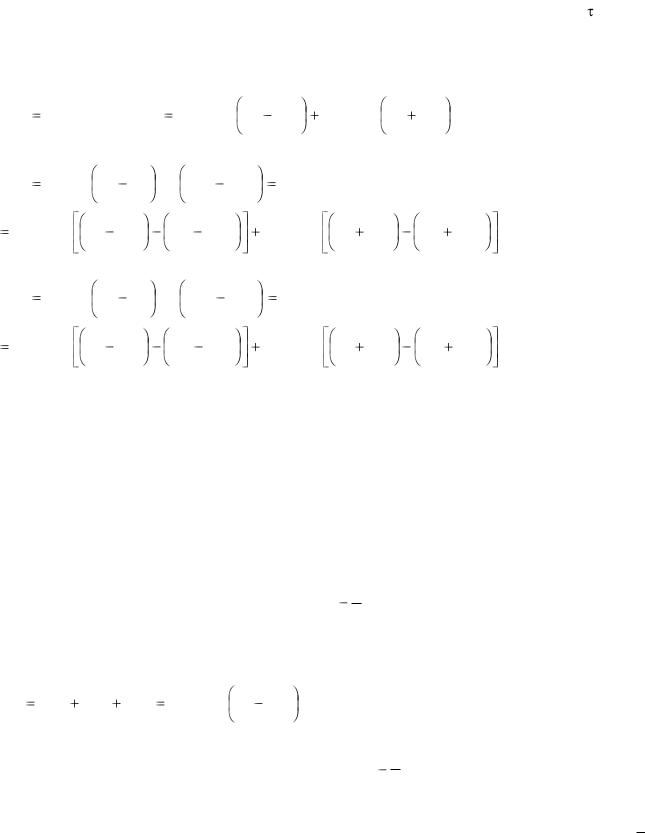
Обратимся к трехфазной обмотке, синусоидальные токи которой образуют симметричную трехфазную систему, и будем при определении ν-й гармоники ее н.с. в точке x (рис. 3-27) учитывать, что по фазе (во времени) ν-е гармоники н.с. фаз В и С сдвинуты относительно v-й гармоники н.с.
|
2π |
4π |
|
|
|
|
|
||
|
|
|
|
|
|||||
фазы А на углы 3 и |
3 , так же как соответствующие токи в фазах обмотки, и что оси фаз B и С |
||||||||
|
|
|
|
ν |
2π |
|
ν |
4π |
|
|
|
|
|
3 и |
3 эл. рад. (для ν-й гармоники соответствует |
||||
сдвинуты относительно оси фазы А на углы |
|
||||||||
νπ эл. рад). Следовательно ν-ю гармонику н.с. трехфазной обмотки в точке х получим как сумму ν-х гармоник н.с. фаз в той же точке, выражения для которых в соответствии с (3-48) и (3-49) имеют следующий вид:
F |
|
|
F |
sin ωt cos |
νxπ |
|
|
1 |
|
|
|
F |
sin ωt |
|
|
νxπ |
|
|
1 |
F |
sin ωt |
νxπ |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
η |
2 |
|
η |
|
|
|
|
|
|||||||||||||||||||||||||||
Atxν |
|
|
мqν |
|
|
|
|
η |
2 |
|
|
|
мqν |
|
|
|
|
|
|
|
|
мqν |
|
|
|
|
; |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
F |
sin ωt |
|
2π |
cos |
|
νxπ |
ν |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Btxν |
|
|
|
мqν |
|
3 |
|
|
|
|
|
|
|
|
η |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
F |
|
sin |
ωt |
νxπ |
|
|
2π |
|
ν |
2π |
1 |
|
F |
sin |
ωt |
|
νxπ |
|
2π |
ν |
|
2π |
; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
мqν |
|
|
η |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
2 мqν |
|
|
|
|
η |
3 |
|
|
3 |
|
|
|||||||||||||||
F |
|
|
F |
sin ωt |
|
4π |
cos |
|
νxπ |
ν |
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ctxν |
|
|
|
мqν |
|
3 |
|
|
|
|
|
|
|
|
η |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
F |
|
sin |
ωt |
νxπ |
|
|
4π |
|
ν |
4π |
1 |
|
F |
sin |
ωt |
|
νxπ |
|
4π |
ν |
|
4π |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
мqν |
|
|
η |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
2 мqν |
|
|
|
|
η |
3 |
|
|
3 |
|
|
|||||||||||||||
Приведенные равенства позволяют сделать следующие выводы.
1. В кривой результирующей н.с. трехфазной обмотки все гармоники с номером, кратным трем, пропадают. В этом мы можем убедиться, обращаясь к первой форме выражения для ν-х гармоник н.с. фаз (произведение синуса на косинус). Для всех трех фаз мы будем иметь косинусы
(cos |
νxπ |
) |
|
2π |
4π |
||
|
|
|
|
|
|
||
одного и того же угла |
η |
; сумма же синусоид, сдвинутых на углы 3 и |
3 и имеющих |
||||
одинаковые амплитуды, равна нулю.
2. Все гармоники с номером ν = 6а—1, где а — любое целое число (1, 2, 3, ...), при сложении
1
дают ν-ю гармонику, вращающуюся с частотой ν n1 , т. е. против вращения первой гармоники. В этом мы можем убедиться, обращаясь ко второй форме выражения для ν-х гармоник н.с. фаз (сумма синусов). Подставляя здесь ν = 5, 11, 17 и т. д., мы получим.
F |
F |
F |
F |
3 |
F |
sin ωt |
νxπ |
|
2 |
η |
|
||||||
txν |
Atxν |
Btxν |
Ctxν |
мqν |
|
, |
||
|
|
|
|
|
|
|
|
1
откуда видим, что ν-я гармоника вращается с частотой ν n1 [ср. с (3-58)].
1
3. Все гармоники результирующей н.с. с номером ν = 6a + 1 вращаются c частотой ν n1 в ту же сторону, что и первая гармоника. В этом случае имеем:
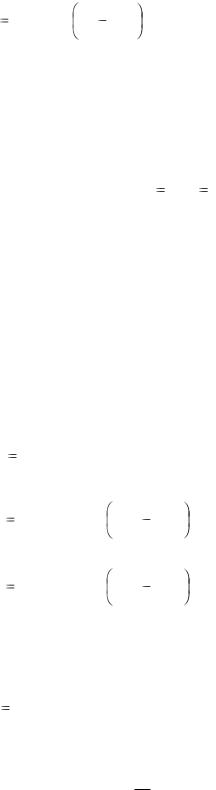
F |
3 |
F |
sin ωt |
νxπ |
|
|
|
|
|
|
|
|
|
||
2 |
|
η |
|
|
|
|
|
|
|
|
|
||||
txν |
мqν |
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Поля, созданные высшими гармониками н.с. обмотки, будут наводить в этой обмотке э.д.с |
|||||||||||||||
той же частоты, |
что и частота э.д.с., |
наведенной первой гармоникой поля. Действительно, ν-я |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n1 |
|
|
|
||
гармоника вращается с частотой |
ν , но она имеет число пар полюсов νр, следовательно, частота |
||||||||||||||
|
|
|
|
|
νp |
n1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn1 |
|
f1 |
|
||||||
|
|
|
|
|
|
|
ν |
|
|
|
|||||
наведенной ею э.д.с. равна |
60 |
|
|
60 |
|
. Очевидно, получится тот же результат, если учесть, что |
|||||||||
|
|
|
|
||||||||||||
потокосцепление фазы обмотки, созданное токами частоты f1 будет во времени изменяться также с частотой f1.
При несимметричной системе токов в фазах трехфазной симметричной обмотки определяются н.с., созданные каждой из симметричных составляющих данной системы токов. Токи прямой и обратной последовательностей создадут круговые н.с , вращающиеся в разные стороны. Результирующей этих н.c. будет эллиптическая вращающаяся н.с., т. е. пространственный вектор результирующей н.с. будет описывать эллипс. Для определения н.с., созданной токами нулевой последовательности, обратимся к предыдущим выражениям для н.с. отдельных фаз. Так как токи нулевой последовательности равны между собой и совпадают по фазе, то эти выражения будут иметь следующий вид:
F |
|
F |
sin ωt cos |
νxπ |
|
|
|
|
|
|
|
Atxν |
|
|
|
|
|
|
|
||||
|
мqν |
|
|
η |
; |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
F |
|
F |
sin ωt cos |
|
νxπ |
|
ν |
|
2π |
|
|
|
|
|
|
|
|
|
|||||
Btxν |
мqν |
|
|
η |
3 |
|
|||||
|
|
|
|
|
; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
F |
sin ωt cos |
|
νxπ |
|
ν |
4π |
|
||
|
|
|
|
|
|
|
|||||
Ctxν |
мqν |
|
|
η |
3 |
|
|||||
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Складывая приведенные значения н.с. отдельных фаз, получим результирующую н.с. Ftxv в точке х. Для всех значений ν, не кратных трем, Ftxv = 0; для значений ν, кратных трем,
F |
3F |
sin ωt cos |
νxπ |
|
|
||||
txν |
мqν |
|
η . |
|
|
|
|
||
Следовательно, токи нулевой последовательности будут создавать пульсирующую н.с. с
2η
пространственным периодом ν , где ν = 3, 9, 15 и т. д. Для исследования ее действия она может быть заменена двумя круговыми н.с. с тем же пространственным периодом, вращающимися в разные стороны и имеющими половинную амплитуду.
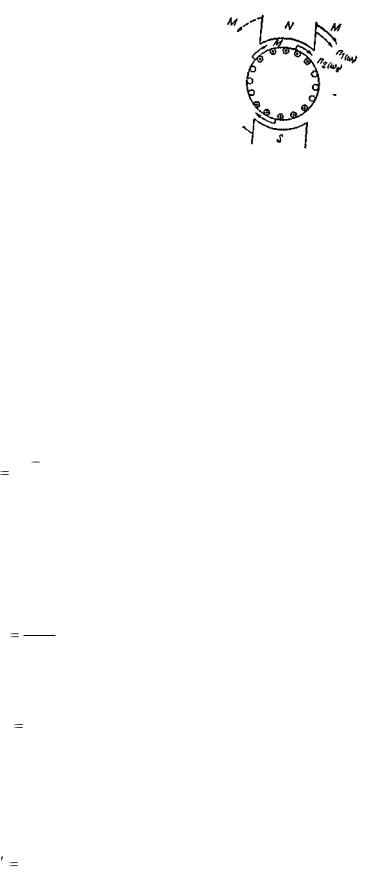
3-5. Принцип действия асинхронного двигателя и его энергетическая диаграмма
Для лучшего понимания принципа действия асинхронного двигателя вначале примем, что его вращающееся поле создается путем вращения двух полюсов (постоянных магнитов или электромагнитов), как показано на рис. 3-28.
Рис. 3-28. К пояснению принципа действия асинхронного двигателя.
В проводниках замкнутой обмотки ротора при этом будут наводиться токи. Их направления указаны на рис. 3-28. Они найдены по правилу правой руки, позволяющему определить направление наведенного тока в проводнике, перемещающемся относительно поля. Пользуясь правилом левой руки, найдем направления электромагнитных сил, действующих на ротор и заставляющих его вращаться. Ротор двигателя будет вращаться в направлении вращения поля. Его частота вращения п2, об/мин, будет меньше частоты вращения поля n1, об/мин, так как только в этом случае возможны наведение токов в обмотке ротора и возникновение электромагнитных сил и вращающего момента.
Частота вращения поля n1 называется синхронной частотой вращения.
Скорость поля относительно ротора (n1 – n2) называется частотой скольжения, а отношение этой частоты к частоте поля, обозначаемое через s,
s |
n1 n2 |
|
|
n1 |
(3-60) |
||
|
|||
|
|
называется скольжением.
Обозначим через М вращающий момент, который нужно приложить к полюсам (рис. 3-28), чтобы вращать их c частотой n1, об/мин, или с угловой частотой, рад/с,
ω1 2πn1
60 . (3-61)
Тогда мощность, необходимая для вращения полюсов,
Pэм Mω1 . (3-62)
На ротор и полюсы действуют одинаковые электромагнитные силы (действие равно противодействию). Они создают одинаковые вращающие моменты, а так как момент, действующий на полюсы (на рис. 3-28 показан пунктирной стрелкой), равен М, той и на ротор действует момент М. Следовательно, механическая мощность, развиваемая ротором,
P2 Mω2 , |
(3-63) |
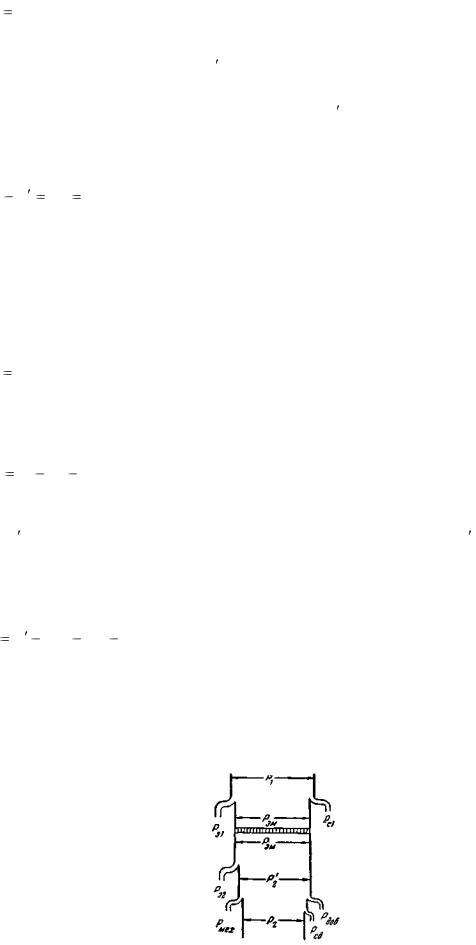
где угловая частота ротора, рад/с,
ω2 |
2πn2 |
|
|
|
|
|
60 . |
(3-64) |
|
|
|||
|
|
|
||||
При работе машины двигателем P2 < Pэм , так как ω2< ω1. |
||||||
Можно считать, что разность мощностей Pэм и |
P2 равна только электрическим потерям в |
|||||
обмотке ротора, имеющей m2 |
фаз при токе в фазе I2 |
и ее активном сопротивлении r2, так как |
||||
потерями в стали ротора, как будет показано, можно пренебречь: |
||||||
P |
P |
P |
m |
I 2 r |
(3-65) |
|
эм |
2 |
э2 |
2 |
2 2 . |
|
|
Мощность Рэм передается вращающимся полем ротору. Она называется электромагнитной мощностью или мощностью вращающегося поля.
В реальной асинхронной машине, работающей двигателем, электромагнитная мощность Рэм равна первичной мощности Р1, подведенной к статору, за вычетом Рэ1 электрических потерь в обмотке статора
P |
m I 2 r |
(3-66) |
|
э1 |
1 1 1 |
||
|
(m1— число фаз; I1 — ток в фазе обмотки статора, r1, — ее активное сопротивление) и потерь в стали статора Pc1, т. е.
P |
P |
P |
P |
, |
(3-67) |
эм |
1 |
э1 |
c1 |
Механическая мощность на валу двигателя P2 (полезная мощность) меньше механической
мощности P2 , развиваемой ротором. Чтобы получить Р2, нужно вычесть из P2 механические потери Pмех на трение в подшипниках и вращающихся частей о воздух, потери Рс.д в зубцах статора и ротора, вызываемые пульсациями поля в них, и небольшие добавочные потери Pдоб, возникающие при нагрузке и вызываемые полями рассеяния статора и ротора:
P2 P2 Pмех Pс.д Pдоб . |
(3-68) |
Наглядное представление о распределении мощностей в асинхронном двигателе дает его энергетическая диаграмма, приведенная на рис. 3-29.
Рис. 3-29. Энергетическая диаграмма асинхронного двигателя.
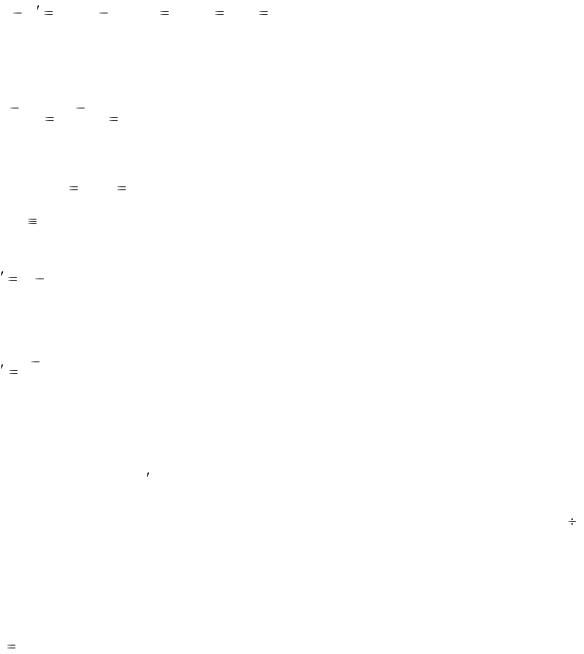
Она соответствует уравнениям (3-67) и (3-68).
Из написанных ранее соотношений (3-62), (3-63) и (3-65) следует:
|
Pэм |
P2 |
|
M (ω1 ω2 ) |
ω1 |
sω1M sPэм Pэ2 |
||||||
|
|
ω |
||||||||||
|
|
|
|
|
|
|
|
1 |
, (3-69) |
|||
|
|
|
|
|
|
|
|
|
||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω1 |
ω2 |
|
|
n1 |
n2 |
|
s |
|
|||
|
ω1 |
|
|
n1 |
|
|||||||
|
|
|
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Pэм |
ω1M |
|
Pэ2 |
|
|
||||
(В равенствах |
|
|
s |
угловая механическая скорость является постоянной при f1 = const; |
||||||||
|
|
|
|
|
|
|
||||||
поэтому Pэм |
|
M, что дало повод назвать величину Рэм "моментом в синхронных ваттах".) Из (3-69) |
||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 |
(1 |
s)Pэм |
|
|
(3-70) |
||||||
|
|
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
1 |
s |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
s |
|
|
э2 . |
|
|
(3-70а) |
|||||
Если скольжение выразить в процентах, то можно написать, что s% от мощности Pэм, полученной ротором от статора через посредство вращающегося поля, расходуется в обмотке ротора на электрические потери [см (3-69)], а оставшаяся часть, равная (1— s) 100% от Pэм, преобразуется в
механическую мощность P2 (3-70), развиваемую ротором. Поэтому асинхронные двигатели выполняются таким образом, чтобы их скольжение было невелико. Оно для нормальных двигателей мощностью от 1 до 1 000 кВт при их номинальной нагрузке составляет приблизительно 6 1%; при больших мощностях обычно s<l%.
Частота вращения поля (синхронная частота) определяется, как указывалось, по формуле (3-
53):
n1 |
60 f1 |
|
|
|
p |
, |
(3-71) |
||
|
||||
|
|
где f — частота тока статора;
р — число пар полюсов его обмотки.
При стандартной в СССР частоте f = 50 Гц синхронные частоты вращения для различных чисел полюсов имеют значения, приведенные в табл. 3-3.
Таблица 3-3
2p |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
24 |
48 |
n1 |
3000 |
1500 |
1000 |
750 |
600 |
500 |
428 |
375 |
250 |
125 |
Частота вращения ротора согласно (3-60), об/мин,
