Асинхронные машины

Рис. 3-12. Размещение лобовых частей трехфазной однослойной обмотки при q = 2.

Рассмотренная обмотка называется катушечной концентрической с лобовыми частями в двух плоскостях. Она в настоящее время применяется сравнительно редко — главным образом для небольших машин (при Р 7 кВт). При большой мощности она требует больше материалов (обмоточной меди и изоляции), чем двухслойная обмотка, так как имеет более длинные лобовые части.

Из однослойных обмоток находят себе также применение, обычно для машин небольшой мощности (до 7 — 10 кВт), равнокатушечные обмотки, схемы которых аналогичны схемам двухслойных обмоток.

г) Двухслойные обмотки.

В настоящее время для статоров асинхронных и синхронных машин преимущественное применение получили двухслойные обмотки. Из них наиболее часто встречаются петлевые двухслойные обмотки. Они состоят из одинаковых катушек, также объединенных в группы. Катушечные стороны закладываются в пазы одна над другой.

Для машин мощностью до 50 100 кВт на статоре берутся полузакрытые (рис. 3-13,б), для машин до 250 300 кВт — полуоткрытые (рис. 3-13,в) и для больших машин — открытые пазы (рис. 3-13,г). Полузакрытые пазы по рис. 3-13,а и б применяются также и для однослойных обмоток. В этом случае изоляционная прокладка (рис. 3-13,б) не нужна.

Рис. 3-13. Пазы статора.

а и б — полузакрытые; в—полуоткрытый, г—открытый.

Число катушек обмотки, очевидно, равно числу пазов Z. Число катушек в катушечной группе при q, равном целому числу, равно q. Для асинхронных машин, как правило, q равно целому числу. Поэтому здесь получаются группы с одинаковыми числами катушек. Для статоров синхронных машин большой мощности при большом числе полюсов часто q равно дробному числу, которое мы

катушечные группы будут иметь неодинаковые числа катушек: часть из них будет иметь b катушек, а другая часть — (b+1) катушек. Те и другие группы должны быть распределены между фазами обмотки таким образом, чтобы фазные э.д.с. были равны по величине и сдвинуты по фазе на 120°.

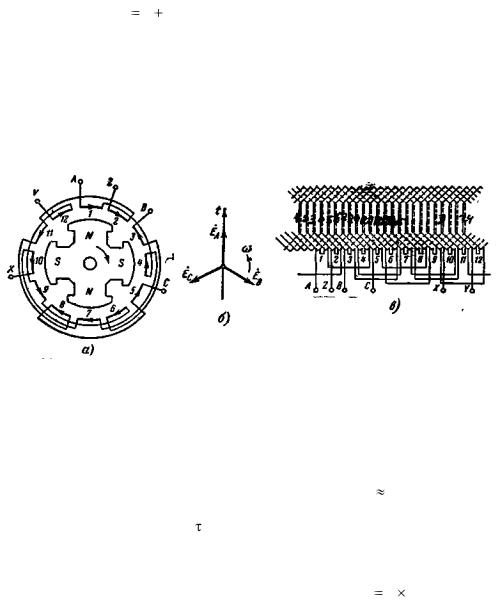
Будем рассматривать петлевые двухслойные обмотки при q, равном целому числу. Схемаразвертка одной из таких обмоток показана на рис. 3-14,в.

Рис. 3-14. Схема трехфазной петлевой двухслойной обмотки при Z = 24; 2p = 4; q = 2; у = 5.

Здесь цифрами обозначены номера катушечных групп, состоящих каждая из двух катушек; катушечные группы каждой фазы соединены последовательно. Шаг обмотки (ширина катушки), измеренный числом пазовых делений, у = 5, тогда как полюсное деление 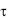= 6. Следовательно,

малых машин катушки часто закладываются целыми группами, поэтому здесь не приходится делать междукатушечные соединения). После этого выполняются междугрупповые соединения, т. е. соединяются между собой группы, составляющие фазы обмоток.

На рис. 3-14,а приведена условная схема той же обмотки, наглядно показывающая соединения между катушечными группами. Последние здесь обозначены короткими дугами с теми же номерами, что и на рис. 3-14,в; стрелками показаны направления э.д.с. в катушечных группах для

момента времени, когда они соответствуют проекциям временных векторов EA , EB , EC на линию времени t (рис. 3-14,б).

На рис. 3-15 представлен статор с катушечными сторонами, заложенными в пазы. Здесь же показаны три катушечные группы, состоящие каждая из трех катушек (q = 3), и дуги 1, 2, 3,..., условно обозначающие катушечные группы.

Рис. 3-15. Статор с уложенными в пазы катушечными сторонами трехфазной двухслойной обмотки

При помощи условной схемы, аналогичной схеме на рис. 3-14,а, легко, находятся междугрупповые соединения, осуществляющие также параллельное или последовательнопараллельное соединение катушечных групп для каждой фазы. Так, например, для фазы А мы можем получить четыре параллельные ветви, соединив параллельно группы 1, 4, 7, 10 или две параллельные ветви, из которых одна будет иметь группы 1 и 4, а другая — 7 и 10.

К преимуществу двухслойной обмотки нужно отнести то, что ее катушки можно заготовить вне машины, хорошо их изолировать (пропитать лаками или особым асфальтобитумным составом) и совершенно готовыми заложить в пазы. При этом применяются открытые пазы, позволяющие выполнить надежную изоляцию на высокие напряжения (до 20000 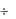24000 B). При полузакрытых и полуоткрытых пазах обмотка обычно выполняется на напряжении до 660 B. В этом случае проводники катушек приходится закладывать в пазы по одному через открытие (щель) паза.

На рис. 3-16 показано размещение лобовых частей двухслойной обмотки.

Рис. 3-16. Лобовые части двухслойной обмотки.

Другим важным преимуществом двухслойной обмотки является то, что ее можно выполнить

сукороченным шагом. При укорочении шага обмотки кривая наведенной в ней э.д.с. при несинусоидальном поле получается более близкой к синусоиде, чем при полном шаге; кривая поля, созданного такой обмоткой, тоже будет более близкой к синусоиде. Кроме того, при двухслойной обмотке с укороченным шагом сокращается расход меди и изоляционных материалов по сравнению

соднослойной обмоткой (рис. 3-11) за счет уменьшения длины лобовых частей (ср. на рис. 3-5,б

лобовые части витков при у = и y < ).

Схемы однослойных равнокатушечных обмоток, имеющих q пазов на полюс и фазу, могут быть получены из схем петлевых двухслойных обмоток, имеющих q/2 пазов на полюс и фазу. Для этого нужно представить себе, что между соседними пазами двухслойной обмотки помещено еще по

одному пазу и в эти пазы вынесены все катушечные стороны, лежащие в нижнем слое Тогда получается схема так называемой цепной обмотки.

Рассмотренная двухслойная обмотка применяется также для фазных роторов асинхронных машин при мощностях до 100 кВт. В этих случаях обычно применяются обмотки с полным шагом, чтобы получить более длинные лобовые части для улучшения условий охлаждения машины.

Волновые двухслойные обмотки находят себе применение для фазных роторов асинхронных машин при мощностях свыше 50 100 кВт. Они выполняются из стержней, закладываемых с торцовой стороны в полузакрытые пазы. Число фаз m2 такой обмотки, как правило, берется равным трем.

Обычная схема волновой двухслойной обмотки представлена на рис. 3-17. Здесь начала и концы фаз равномерно смещены по окружности ротора, так же как и перемычки фаз (I—II, III—IV, V— VI), что облегчает выполнение отводов к контактным кольцам и вместе с тем позволяет сохранить статическую уравновешенность ротора (совпадение центра тяжести ротора с его осью вращения). В последние годы волновые двухслойные обмотки применяются также для статоров крупных синхронных машин, имеющих большое число полюсов (генераторы, работающие на мощных гидроэлектрических станциях). В этом случае они обычно выполняются при q, равном дробному числу.

Рис. 3-17. Роторная стержневая обмотка при Z = 24; 2р = 4; q = 2 (показана только одна фаза).

д) Обмотки для короткозамкнутых роторов.

Такие обмотки, как правило, выполняются в виде беличьих клеток, состоящих из стержней и замыкающих их на торцах колец (рис. 3-18).

Рис. 3-18. Короткозамкнутая обмотка ротора в виде беличьей клетки

В последние годы для машин до 100 кBт они обычно выполняются путем заливки расплавленного алюминия в пазы ротора. При этом одновременно отливаются и короткозамыкающие торцовые кольца вместе с вентиляционными крыльями (рис. 3-19).

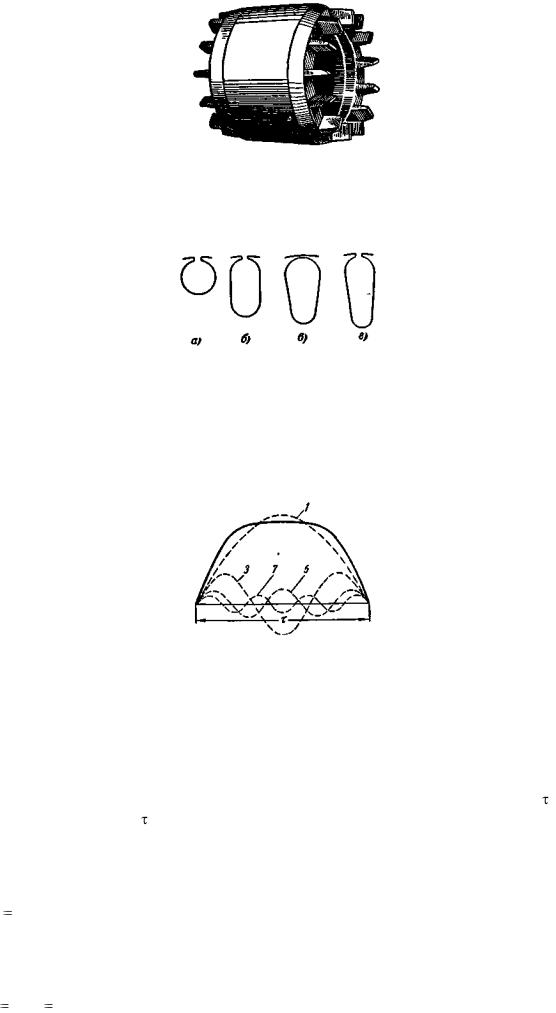
Рис. 3-19. Алюминиевая короткозамкнутая обмотка ротора.

Пазы ротора показаны на рис. 3-20.

Рис. 3-20. Пазы ротора.

е) Электродвижущие силы при несинусоидальном поле.

На рис. 3-21 представлена кривая поля (сплошная линия), созданного, например, вращающимися полюсами.

Рис. 3-21. Кривая поля и ее гармоники.

Ее можно разложить на гармоники, причем вследствие симметрии кривой относительно оси абсцисс и максимальной ординаты в разложении будут иметь место только синусоиды нечетного порядка, показанные на рис 3-21 пунктиром.

Все гармоники поля вращаются относительно статора с одной и той же частотой, равной частоте вращения полюсов. Полюсное деление первой или основной гармоники равно , полюсное деление ν -й гармоники равно /ν. Таким образом, ν-я гармоника поля имеет в ν раз больше полюсов, чем первая гармоника.

Электродвижущая сила, наведенная в фазе обмотки ν-й гармоникой поля, равна:

где

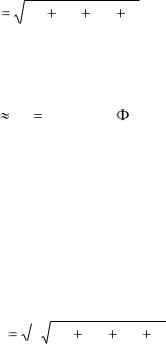
Из табл. 3-1 следует, что путем выбора шага мы можем значительно уменьшить амплитуды высших гармоник в кривой фазной э.д.с.

Действующее значение фазной э.д.с.

Так как в обычных случаях амплитуды высших гармоник сравнительно с амплитудой первой гармоники невелики, мы можем практически считать:

где f1 и k01 определяются для первой гармоники, а Ф (индекс «м» здесь и в последующем опускаем)

— по первой гармонике кривой поля (или приближенно по действительной кривой поля).

Гармоники фазных э.д.с. трехфазной обмотки с номером, кратным трем, совпадают по фазе, прочие гармоники фазных э.д.с. (5, 7, 11, 13. 17, ...) той же обмотки будут сдвинуты по фазе на 120°.

Следовательно, при соединении обмотки звездой в линейной э.д.с. все гармоники с номером, кратным трем, пропадают:

При соединении обмотки треугольником мы также не будем иметь в линейном напряжении гармоник с номером, кратным трем, так как при таком соединении все эти гармоники по контуру, составленному из трех фаз об мотки, будут в любой момент времени направлены в одну и ту же сторону (фазы обмотки для гармоник с номером, кратным трем, могут рассматриваться как последовательно соединенные генераторы).

3-4. Намагничивающие силы обмоток

а) Однофазная обмотка.

На рис. 3-22,а показаны статор и ротор двухполюсной асинхронной машины с воздушным зазором между ними. который всегда делается равномерным для асинхронных машин. На статоре в пазах помещена только одна катушка, имеющая ширину, равную полюсному делению. Если пропустить по катушке ток, то она создаст двухполюсное магнитное поле, индукционные линии которого показаны на рис. 3-22,а.

Рис. 3-22. Намагничивающая сила катушки.

Намагничивающая сила, действующая по замкнутому контуру, образованному любой индукционной линией, равна полному току, охваченному этим контуром. Следовательно, все н.с., действующие по пунктирным контурам, будут одинаковы.

Так как обе части машины симметричны относительно плоскости, проходящей через катушечные стороны, то на каждую половину магнитной цепи будет приходиться половина н.с. катушки и ее можно считать за н.с. приходящуюся на полюс.

Развернем внутреннюю окружность статора в прямую линию, как показано на рис. 3-22,б. Здесь жирная линия представляет собой кривую распределения н.с. вдоль окружности статора. Из сказанного следует, что н.с. распределена равномерно. Если пренебречь магнитным сопротивлением стальных участков, то под кривой н.с. можно понимать кривую распределения магнитного напряжения воздушного зазора. Такой же вид в этом случае будет иметь кривая распределения индукции в воздушном зазоре или кривая поля машины.

Если по катушке проходит переменный синусоидальный ток, то поле будет также переменным; оно будет пульсировать по оси катушки.

Намагничивающая сила катушки на полюс при максимальном значении тока 2I к равна:

где wк — число витков катушки.

Можно указанную кривую н.с. заменить ее гармониками, из которых на рис. 3-22,б показаны первая, третья и пятая. Амплитуда первой (или основной) гармоники

амплитуда v-й гармоники

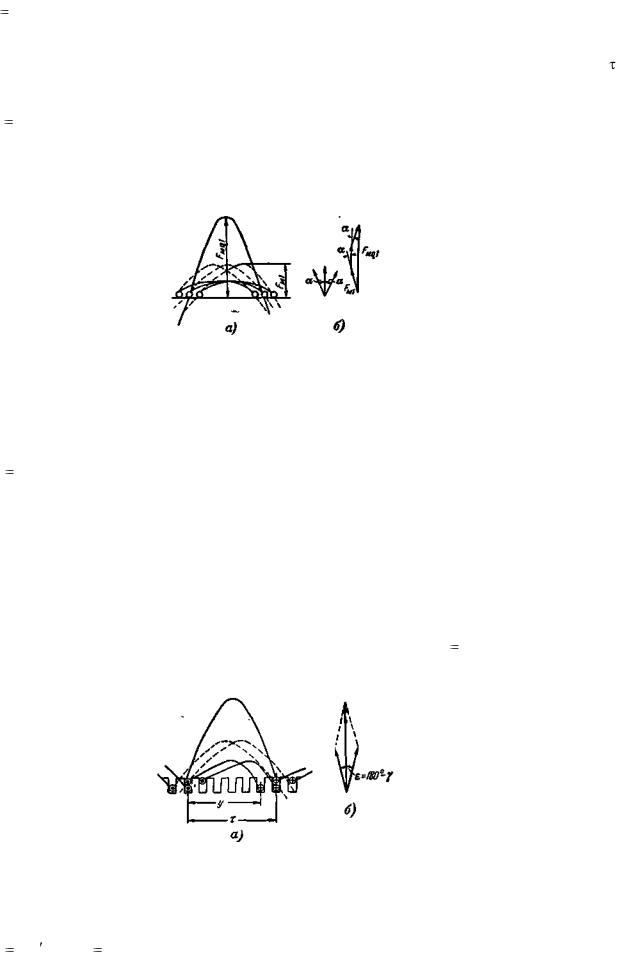
Намагничивающая сила катушечной группы, состоящей из q катушек шириной , вычисленная по первым гармоникам н.с. каждой катушки (рис. 3-23,б),

где k01 — коэффициент распределения, который рассчитывается, так же как для э.д.с., по (3-18), что следует из сопоставления рис. 3-23,б и рис. 3-9.

Рис. 3-23. Намагничивающие силы q катушек (а) и векторная сумма н.с. отдельных катушек (б).

Намагничивающая сила той же катушечной группы, но рассчитанная для ν-х гармоник н.с. катушек,

где kpv определяется по (3-28).

При двухслойных обмотках, которые выполняются обычно с укороченным шагом, необходимо при определении н.с. учесть укорочение шага. На рис. 3-24,а показана часть одной фазы двухслойной обмотки с укороченным шагом. Рассматривая токи верхнего и нижнего слоев, можно установить, что верхние и нижние слои как бы образуются из катушек шириной 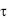(см. также рис. 3-

Рис. 3-24. Намагничивающая сила одной фазы двухслойной обмотки.

Следовательно, н.с. одной фазы двухслойной обмотки на один полюс равна:

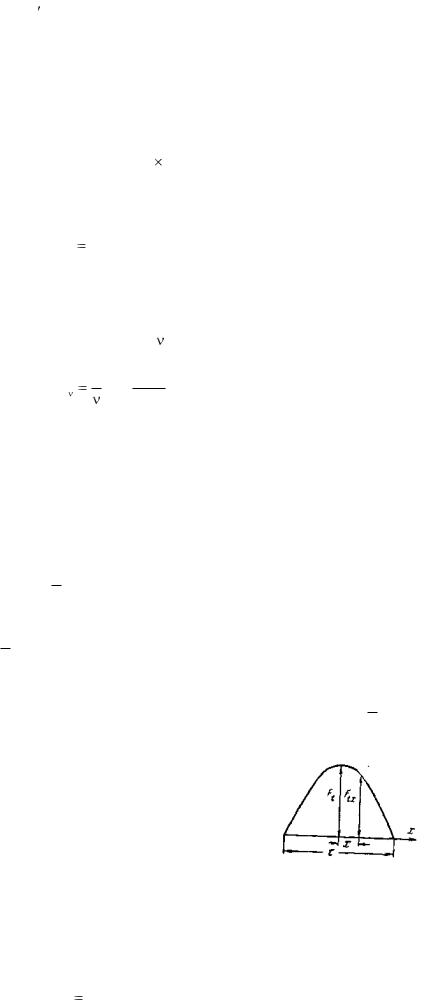
где Fмq1 — амплитуда н.с. "катушечной группы" верхнего или нижнего слоя;

wк — удвоенное число витков катушки двухслойной обмотки;

kу1 — коэффициент укорочения, который рассчитывается по (3-10), как и для э.д.с., что следует из рис. 3-24,б.

p (3-38)

где k01=kр1kу1 обмоточный коэффициент для первой гармоники н.с.

Для амплитуды -й гармоники н.с. мы можем написать:

F 1 0,9I wk0 ν ,

где k0ν — обмоточный коэффициент для ν-й гармоники н.с., который определяется, так же как для ν- й гармоники э.д.с., по (3-26) — (3-28).

Из табл. 3-1 можно видеть, что укорочение шага позволяет значительно снизить амплитуды высших гармоник в кривой н.с. При y = 0,83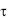наиболее заметно уменьшаются амплитуды пятой и седьмой гармоник, следующие по величине после третьей гармоники, а так как последняя пропадает в н.с. трехфазной обмотки (см. § 3-4,б), то обычно и выбирают указанное значение шага у. Пульсирующую по оси фазы н.с., синусоидально распределенную и имеющую при максимальном

токе 2I амплитуду Fмq1, можно заменить двумя синусоидально распределенными н.с., но вращающимися в разные стороны с одинаковыми частотами и имеющими неизменные амплитуды

1

2 Fмq1 что доказывается следующим образом.

Обратимся к рис. 3-25, где показана кривая пульсирующей н.с. с амплитудой Ft1 = Fмq1sinωt, соответствующей моменту t, когда ток в фазе равен 2 Isinωt.

Рис. 3-25. Кривая пульсирующей н.с.

Значение н.с., соответствующей точке окружности статора, сдвинутой на x относительно оси фазы, будет: