
КУРС ЛЕКЦИЙ ПО СОПРОМАТУ
.pdf
Требуется вычислить интеграл Мора i MF Mi dz EIx
Грузовая эпюра MF имеет площадь, равную АF с центром тяжести в точ-
ке С.
Площадь |
его |
элементарной площадки на |
координате z равна |
||||||||||||||
dAF MF dz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Высота единичной эпюры на этой же координате равна |
|
i z tg . |
|||||||||||||||
M |
|||||||||||||||||
С учетом этого MF |
|
idz z tg dAF . |
|
|
|
||||||||||||
M |
|
|
|
||||||||||||||
Здесь z dAF - это статический момент SX грузовой эпюры MF, который |
|||||||||||||||||
можно найти |
также |
по |
формуле SX zC AF . Следовательно |
||||||||||||||
MF |
|
idz zC tg AF . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
M |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из рисунка видно, что |
|
zC tg |
|
|
C , что является высотой единичной |
||||||||||||
|
M |
||||||||||||||||
эпюры на координате точки С. |
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, |
интеграл |
MF |
|
idz AF |
|
C , |
а формула определе- |
||||||||||
M |
M |
||||||||||||||||
ния перемещений по способу Верещагина принимает вид i AF MC
EIx
Итак, интеграл Мора равен произведению площади грузовой эпюры на ординату единичной эпюры, взятую под центром тяжести грузовой эпюры.
Примечания:
1.Используется способ Верещагина только при расчетах прямолинейных систем.
2.Если система имеет несколько силовых участков, то перемножаются грузовые и единичные эпюры на каждом участке.
3.Перемножаются грузовые и единичные эпюры, расположенные на одном основании.
4.Если эпюра имеет сложную форму, то она разбивается на простые фигуры – прямоугольник, треугольник и пр.
5.Если перемножаемые эпюры имеют разные знаки, то их произведение отрицательно, а если одинаковые знаки – то произведение положительно.
6.Если грузовая эпюра имеет прямолинейную форму, то перемножение можно производить в обратном порядке, т.е. площадь единичной эпюры умножаем на ординату грузовой эпюры, взятую под центром тяжести единичной эпюры.
61

Пример Определить способом Верещагина прогиб и угол поворота сечения В.
Решение:
1. Для определения yB образуем 1-ю вспомогательную систему, где в точку В прикладываем единичную силу F .
Для определенияB образуем 2-ю вспо-
могательную систему, где в точку В прикладываем единичный момент M .
2. Строим для заданной системы грузовую эпюру MF, для 1-й вспомогательной системы единичную эпюру M1 и для 2-й
вспомогательной системы единичную
эпюру M2 .
3. Решаем интеграл Мора способом Верещагина, т.е. вычисляем искомые перемещения, перемножая соот-
ветствующие эпюры:
|
MF |
|
|
|
|
|
|
|
|
Fl l |
|
2 |
l |
|
Fl3 |
|
||||||||
1 yB |
M |
1 |
|
dz |
|
|
2 |
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
EIx |
|
|
|
|
EIx |
|
|
|
|
3EIx |
|
||||||||||||
|
|
MF |
|
|
|
|
|
|
|
|
|
Fl l |
|
1 |
|
Fl2 |
|
|||||||
2 B |
M |
2 |
dz |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
EIx |
|
|
|
|
EIx |
|
|
|
2EIx |
|
|
|||||||||||||
62
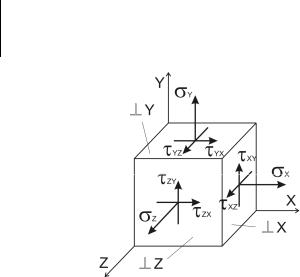
8 ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ
Напряженное состояние в произвольной точке тела характеризуется нормальными и касательными напряжениями, зависящими от ориентации элементарной площадки в этой точке.
8.1 Напряженное состояние в точке
Выделим в произвольной точке тела элементарный кубик. В общем виде на его гранях возникает девять составляющих напряжений. Их совокупность называют тензором напряжений.
σX |
τXY |
τXZ |
|
τYX |
σY |
τYZ |
- тензор напряжений |
τZX |
τZY |
σZ |
|
Обозначения: первый индекс означает, к какой площадке относится напряжение. Второй индекс – вдоль какой оси направлено напряжение.
Например: τZY относится к площадке, перпендикулярной оси Z и направлено вдоль оси Y,
σXX = σX относится к площадке, перпендикулярной оси X и направлено вдоль оси X.
Из условия равновесия τXY = τYX, τXZ = τZX, τYZ = τZY. Это – закон пар-
ности напряжений.
63
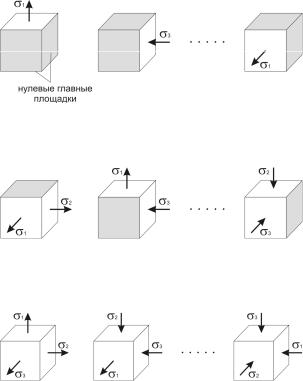
Правило знаков: все изображенные на рисунке напряжения положительны.
При определенном расположении кубика касательные напряжения на всех его площадках равны нулю. Такие площадки называют главными, а нормальные напряжения на этих площадках – главными напряжениями.
Нумеруют эти напряжения из условия, что σ1 > σ2 > σ3.
Различают
- линейное напряженное состояние (σ1 ≠ 0 или σ3 ≠ 0)
- плоское напряженное состояние (σ1 = 0 или σ2 = 0 или σ3 = 0)
- объемное напряженное состояние (σ1 ≠ 0; σ2 ≠ 0; σ3 ≠ 0)
64
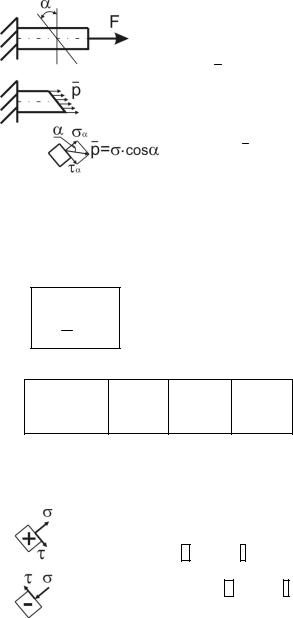
|
8.2 |
Линейное напряженное состояние |
|
|
|||||||||||||
|
|
|
|
Определим |
напряжения |
на |
произвольно |
||||||||||
|
|
|
ориентированной площадке. |
|
|
||||||||||||
|
|
|
|
Проведем сечение под углом α к |
|||||||||||||
|
|
|
вертикали. В этом сечении имеет место напря- |
||||||||||||||
|
|
|
жение |
p |
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Площадь |
наклонного |
сечения равна |
|||||||||||
|
|
|
A |
|
|
A |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
cos |
|
|
|
|
|
|
||||||
|
|
|
|
Тогда |
p |
|
F |
|
F |
cos cos . |
|||||||
|
|
|
|
A |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|||
|
Нормальное |
напряжение |
|
|
|
|
на |
|
|
|
площадке |
равно |
|||||
cos cos cos2 , |
|
|
|
а |
касательное |
|
напряжение |
||||||||||
|
cos sin |
|
sin2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, напряжения при линейном напряженном состоянии на произвольной площадке определяют по формулам:
cos2
2 sin2
Для некоторых значений угла α напряжения составляют:
α, град |
00 |
450 |
900 |
σα |
σ |
σ/2 |
0 |
τα |
0 |
σ/2 |
0 |
Так, при α=450 касательное напряжение имеет максимальное значение.
Это напряжение и обуславливает разрушение хрупких материалов под углом
α≈450.
Правило знаков
для σ – по растянутым (сжатым) волокнам: растяжение +, сжатие -.
для τ – по направлению вращения: по часовой стрелке +, против -.
65
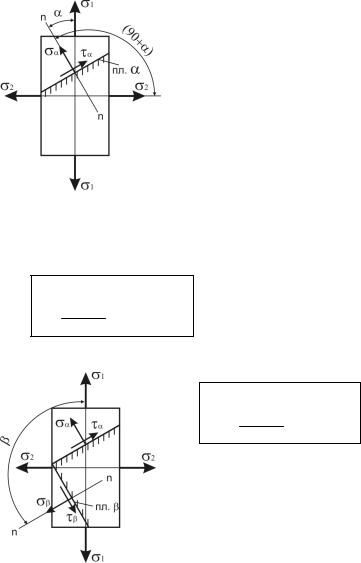
8.3 Плоское напряженное состояние
|
|
|
|
|
|
|
|
|
При плоском |
напряженном состоянии |
||||||
|
|
|
|
|
|
|
|
имеется два главных напряжения σ1 и σ2, не |
||||||||
|
|
|
|
|
|
|
|
равных нулю. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Пусть требуется определить напряжения |
|||||||
|
|
|
|
|
|
|
|
на площадке α. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Угол α откладываем от наибольшего |
|||||||
|
|
|
|
|
|
|
|
напряжения σ1 |
против часовой стрелки. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
I |
II |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
I |
II |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
где индексы I и II показывают, что |
|||||||
|
|
|
|
|
|
|
|
напряжения возникают соответственно от σ1 и |
||||||||
|
|
|
|
|
|
|
|
σ2 |
|
|
|
|
|
|
|
|
I |
1 cos |
2 |
; |
II |
2 |
cos |
2 |
(90 ) 2 sin |
2 |
|
||||||
|
|
|
|
|
||||||||||||
I |
|
1 |
sin2 ; |
II |
|
2 |
sin2(90 ) |
2 |
sin2 |
|||||||
|
|
|
||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||
Итак, получим напряжения на площадке α
1 cos2 2 sin2
1 2 sin2 2
Аналогично определим напряжения на площадке β, принимая β=90+α.
1 sin2 2 cos2
1 2 sin2 2
Выводы:
1)σα+σβ= σ1+σ2=const
2)τα=-τβ
3)σ → max при α=πn, при этом τ=0
4)τ → max при α=π/4
При вычислениях σ и τ различают прямую и обратную задачи.
Прямая задача. |
Дано: σ1, σ2, α, β |
|
Найти: σα, τα, σβ, τβ |
|
66 |
Обратная задача. Дано: σα, τα, σβ, τβ Найти: σ1, σ2, α, β
8.3.1 Прямая задача
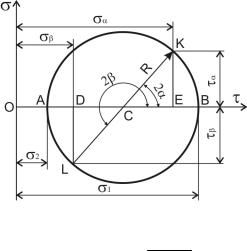
Прямая задача решается либо по формулам, либо графически с помощью круга Мора.
Откладываем отрезки ОА=σ2 и ОВ=σ1. Из точки С (середина отрезка АВ)
проводим окружность радиусом R AC 1 2 . Через точку С под углом
|
|
|
|
|
|
2 |
|
|
1 2 |
|
|||||
2α проводим линию LK. |
Получаем, что CE R cos2 |
cos2 . |
|||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
1 2 |
|
1 2 |
|
2 |
|
|||
Тогдаотрезок ОЕ ОА АС СЕ 2 |
|
|
|
cos2 |
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
||||
2 |
1 2 |
(1 cos2 ) 2 |
|
1 2 |
2cos2 2 1 |
cos2 |
|||||||||
|
|
||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
2 cos2 1 cos2 2 sin2
Аналогично можно доказать, что OD=σβ, KE=τα, DL=τβ.
8.3.2 Обратная задача
Откладываем отрезки ОD=σβ, ОE=σα, EK=τα и DL=τβ.
Точки K и L соединяем прямой, получаем точку С, вокруг которой проводим окружность радиусом R=CK.
Получаем ОА=σ2, ОВ=σ1. и угол 2α, равный углу KCE.
67
8.4Объемное напряженное состояние
Вобщем случае на гранях произвольно ориентированного кубика действует девять напряжений, из них шесть – независимых.
Напряженное состояние элементарного кубика определяется тензором напряжений:
σX |
τXY |
τXZ |
|
τYX |
σY |
τYZ |
- тензор напряжений |
τZX |
τZY |
σZ |
|
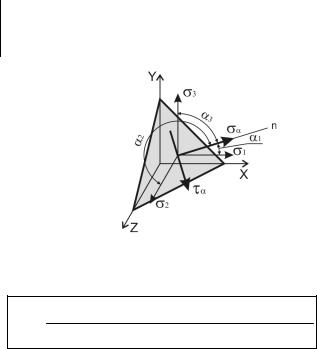
В общем случае, зная главные напряжения σ1, σ2, σ3, можно вычислить σα, τα по формулам:
1 cos2 1 2 cos2 2 3 cos2 3

 1 cos 1 2 2 cos 2 2 3 cos 3 2
1 cos 1 2 2 cos 2 2 3 cos 3 2
где α1, α2, α3 – соответственно углы между нормалью к площадке α и направлением напряжений σ1, σ2, σ3.
Анализ уравнений показывает, что
max |
1, min |
3, max |
|
1 3 |
. |
|
|||||
|
|
|
2 |
|
|
Для проверки на прочность материала при сложном напряженном состоянии необходимо уметь определять напряжения на октаэдрической площадке, где α1=α2=α3=α. При этом cos2 α1+ cos2 α2+ cos2 α3=1, следовательно cos2 α=1/3.
68
|
окт |
1 |
2 |
3 |
|
|
|
|
Тогда |
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
1 2 2 |
2 |
3 2 |
3 |
1 2 |
|||
окт |
||||||||
|
|
3 |
|
|
|
|
|
|
8.5 Деформации при сложном напряженном состоянии. Обобщенный закон Гука
Известно, что относительная продольная деформация равна , от-
E
носительная поперечная деформация равна ,
E
где - коэффициент Пуассона.
|
|
При |
|
объемном |
напряженном состоянии: |
||||||
1 |
|
a |
; |
2 |
|
b |
; |
3 |
|
c |
- главные относительные |
|
|
|
|||||||||
|
|
a |
|
|
b |
|
|
c |
|||
удлинения.
Причем, например ε1= ε1-1+ ε1-2+ ε1-3, где ε1-1 - это удлинение в направлении 1 от
напряжения σ1, ε1-2 - это удлинение в направлении 1 от
напряжения σ2,
ε1-3- это удлинение в направлении 1 от напря-
жения σ3.
Эти удлинения составляют соответственно
1 1 |
|
1 |
; 1 2 |
2 |
; 1 3 |
|
3 |
. |
|
||||||||
|
|
|
|
||||||||||||||
|
|
E |
|
|
|
|
|
E |
|
|
|
|
E |
|
|||
Тогда 1 |
|
1 |
|
2 |
|
|
3 |
|
1 |
|
1 |
2 3 |
|||||
E |
E |
E |
|
||||||||||||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
|||||
Аналогично можно получить формулы для определения ε2=и ε3. Итак, обобщенный закон Гука для изотропного тела имеет вид:
1 |
|
1 |
|
|
1 2 3 |
||
|
|
|
|||||
|
|
|
|
E |
|||
2 |
|
1 |
|
2 1 3 |
|||
|
|
||||||
|
|
|
|
E |
|||
3 |
|
1 |
3 1 2 |
||||
|
|||||||
|
|
|
|
E |
|||
69

Из полученной формулы можно получить выражения для плоского напряженного состояния, считая одно из главных напряжений равным нулю, и для линейного напряженного состояния, считая два главных напряжения равными нулю.
8.5.1Объемная деформация
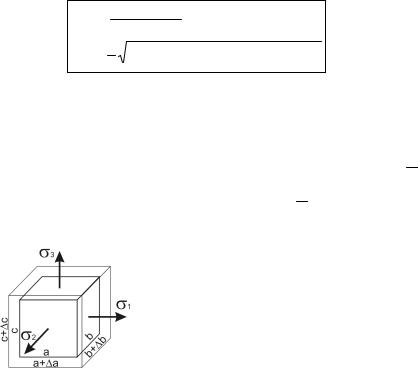
Получим формулу относительной объемной деформации εV. Объем тела до деформации составлял V0=abc, после деформации
V (a a)(b b)(c c) abc(1 |
a |
)(1 |
b |
)(1 |
c |
) V (1 |
1 |
) |
||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
b |
c |
0 |
|
||||
(1 2)(1 3) V0(1 1 2 |
|
|
|
|
|
|
||||||||||||
3 |
1 2 |
1 3 1 |
2 3) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
V V0 |
|
|
|
|
пренебрегаемввидумалости |
|
|
|||||||
|
Тогда V |
1 2 3 , или окончательно |
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
V0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
|
1 2 |
1 2 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выводы:
1) Если μ=0,5, то εV=0, то есть изменения объема тела не происходит.
2) Если σ1 =σ2 =σ3=σ, то V 1 2 3 ,
E K
где K |
E |
- объемный модуль упругости. |
|
3(1 2 ) |
|||
|
|
70
