КУРС ЛЕКЦИЙ ПО СОПРОМАТУ

Опуская решение, получаем RA=5 кН, HA=10 кН, RB=10 кН.

2.Выделяем на раме силовые участки. Границами участков являются точки приложения всех внешних усилий, начало-конец распределенных нагру-

зок, а также узлы рамы. В нашем примере 5 силовых участков.

3.Составляем уравнения внутренних усилий на каждом участке.

1 участок: 0 ≤ z1 ≤ a

3 участок: 0 ≤ z3 ≤ a N=0

QY=0

MX=0

4 участок: 0 ≤ z4 ≤ a N=0

QY=0 MX=10 кН·м

5 участок: 0 ≤ z5 ≤ 2a N=0

QY=-RB+q z5

MX=M+RB z5- q z5 z5/2

при z5=0 QY=-RB=-5 кН, MX=M=10 кН·м

при z5=2a QY=-RB+q 2a=5 кН, MX=M+RB a- q a2/2=10 кН·м

На пятом участке эпюра QY пересекает нулевую линию, определим экстремальное значение изгибающего момента МХ.

Из уравнения QY=-RB+q z0=0 найдем z0=1 м.

На этой координате MX=M+RB z0- q z0 z0/2=12,5 кН·м. 4. Строим эпюры:

21

2.7 Эпюры продольных сил N, поперечных сил QY и QX, изгибающих моментов MX и МY, крутящих моментов MK в пространственных брусьях

Правило знаков аналогично принятому ранее.

Эпюры внутренних усилий строим в тех плоскостях, в которых действуют усилия:

QY и MX – в плоскости YOZ;

QX и MY – в плоскости XOZ;

N и MK – строим в любой плоскости с указанием знака.

Кроме того, эпюры MX и MY следует строить со стороны сжатых воло-

кон.

Для определения знаков внутренних усилий можно также использовать

«плавающую» систему координат.

В том случае, если сечение перемещаем слева - направо, то есть, отбрасываем правую часть бруса, то в точку рассечения силового участка вставляем правую систему координат, при обратном перемещении сечения – левую систему координат.

22

В таком случае используется правило знаков, принятое для уравнений статики:

-сила, совпадающая с положительным направлением оси, положительна и наоборот;

-момент, действующий относительно оси против часовой стрелки, положителен и наоборот (смотрим навстречу координатной оси).

Пример

Дано: M=20 кН·м, F=15 кН, q=10 кН/м, a=1 м.

Требуется: построить эпюры всех внутренних усилий.

Решение: Опорные реакции не определяем, т.к. будем отбрасывать ту часть бруса, где расположена опора. Брус имеет четыре силовых участка.

Определяем внутренние усилия:

1 участок: 0 ≤ z1 ≤ a N=0

QX=0

QY=qz1

MX=-qz1· z1 /2 MY=0

MK=0

qa·a/2=-5 кН·м

2 участок: 0 ≤ z2 ≤ 2a N=qa=10 кН

QX=0

QY=0

MX=-qa·a /2=-5 кН·м MY=0

MK=0

3 участок: 0 ≤ z3 ≤ a N=0

QX=-F=-15 кН QY=-qa=-10 кН

MX=-qa· z3

MY=Fz3

MK=-qa·a /2=-5 кН·м при z3=0 MX=0, MY=0

при z3=a MX=-qa2=-10 кН·м MY=Fa=15 кН·м

4 участок: 0 ≤ z4 ≤ a N=0

23

QX=-F=-15 кН QY=-qa=-10 кН

MX=-qa(a+z3)

MY=F(a+z3)

MK=-qa·a/2=-5 кН·м

при z4=0 MX=-qa2=-10 кН·м MY=Fa=15 кН·м при z4=a MX=-q2a2=-20 кН·м MY=F2a=30 кН·м

Далее строим эпюры:

24

3 РАСТЯЖЕНИЕ (СЖАТИЕ)

Растяжение или сжатие стержня возникает от действия внешних сил, направленных вдоль его оси.

где A – площадь поперечного сечения стержня, м2;

σ – нормальное напряжение (внутренняя сила, отнесённая к единице площади), Па.

При упругих деформациях между σ и ε существует зависимость, описы-

Физический смысл модуля Юнга:

Модуль упругости численно равен напряжению, при котором абсолютное удлинение стержня равно его первоначальной длине, т.е. Е=σ при ε=1.

25

μ – это коэффициент Пуассона, характеризует упругие свойства материала.

Диапазон изменения коэффициента Пуассона: 0<μ<0,5. Например, для стали μ≈0,3; для каучука μ≈0,5; для пробки μ≈0.

3.1 Напряжения и деформации при растяжении (сжатии)

Деформацию можно определять также по формуле l N , (3.9) c

где c EA - жесткость стержня. l

В случае, если продольная сила N или площадь А сечения стержня не постоянны по длине l, деформацию стержня определяют по формуле

26

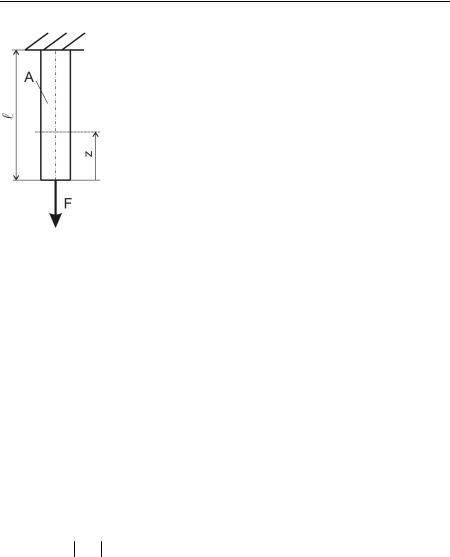
Пример:

Дано: F, A, l и γ – вес единицы объема материала стержня.

Определить: абсолютное удлинение стержня с учетом его собственного веса.

Решение:

1. Определим продольную силу в произвольном сечении стержня: N=F+γAz,

где γAz – вес части стержня, отсеченной координатой z.

2.Определим деформацию стержня:

3.2 Расчеты на прочность при растяжении (сжатии)

При расчетах на прочность максимальное напряжение, возникающее в стержне, должно быть не больше допускаемого напряжения.

Если р с , то при растяжении max р , при сжатии min c .

Различают расчеты на прочность:

1.Проектировочный расчет (подбор сечения).

2.Определение допускаемой нагрузки.

3.Проверочный расчет (проверка условия прочности).

27

Пример

Дано: F1=10 кН, F2=30 кН, А1=1,5 см2, А2=3,5 см2, р =50 МПа,

c =100 МПа.

Требуется: выполнить проверочный расчет.

Решение:

1 участок: N1=-F1=-10 кН

Т.к. |-66,7 МПа|<100 МПа, то условие прочности на I участке выдержа-

но.

2 участок: N2=-F1+ F2=20 кН

57,1МПа>50 МПа, следовательно, на II участке – перенапряжение, ко-

торое составляет 57,1 50100% 14%.

50

Перенапряжение допускается в пределах 5%.

Вывод: условие прочности не выдержано.

28

3.3 Расчеты на жесткость при растяжении (сжатии)

При расчетах на жесткость абсолютное удлинение стержня не должно превышать допускаемого удлинения.

l EANl l - условие жесткости при растяжении (сжатии),

где l - допускаемое удлинение стержня.

Пример

Дано: F1=20 кН, F2=10 кН, l1=1,5 м, l2=1 м, [Δl]=2,5 мм, Е=100 ГПа, [σ]=120 МПа.

Требуется: выполнить проектировочный расчет по условию жесткости.

Решение: составим уравнение полной деформации стержня

Принимаем А=2 см2.

Расчет на жесткость обязательно проверяют на условие прочности.

Условие прочности выдержано.

29

4 СДВИГ (СРЕЗ)

Сдвиг возникает в случае действия на брус двух близко расположенных, равных по величине и противоположно направленных сил, перпендикулярных к оси бруса.

От действия внешних сил F в сечении бруса возникает внутреннее усилие - поперечная сила Q, а в каждой точке сечения – касательное напряжение τ.

По условию статики dA Q.

A

Считая, что τ =const по всей площади A, имеем τ·A=Q,

откуда Q - формула определения касательных

A

напряжений при сдвиге.

4.1 Деформации при сдвиге

Деформации при сдвиге характеризуются:

-абсолютным сдвигом ΔS, м;

-относительным сдвигом (углом сдвига) γ, рад.

Ввиду малости деформации tg S . a

По закону Гука между напряжением τ и относительной деформацией γ существует линейная зависимость τ=G·γ, где G – модуль

сдвига (модуль упругости II рода), Па.

Модуль Юнга и модуль сдвига связаны зависимостью G E , где

2(1 )

μ – коэффициент Пуассона.

Определим абсолютную деформацию при сдвиге:

где GA – жесткость сечения при сдвиге.

30