КУРС ЛЕКЦИЙ ПО СОПРОМАТУ

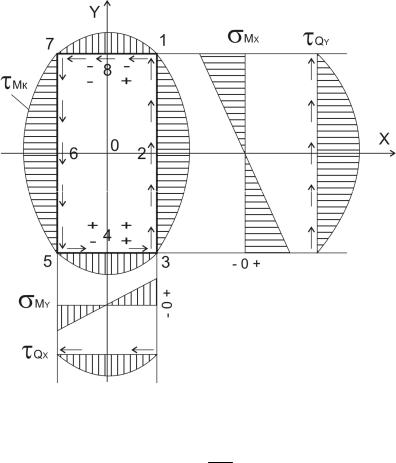
Напряжения от продольный силы, поперечных сил и изгибающих моментов определяем по известным формулам.

Касательное напряжение от крутящего момента в валах некруглого се-

чения определяют по формуле max MK , причем на середине большей

WK

стороны прямоугольника напряжение максимально, а на середине меньшей стороны равно τ=γτmax.

Здесь WК – момент сопротивления при кручении, например, для прямоугольного сечения WК=αhb2;

α, γ – коэффициенты, зависящие от соотношения h/b (даны, например, в [1]);

h– наибольшая сторона прямоугольника.

Впрямоугольном сечении несколько потенциально опасных точек. Выберем одну опасную точку из угловых, одну на середине большей стороны и одну на середине меньшей стороны. Это соответственно точки 3, 2 и 8. Вычислим напряжения в этих точках:

91

11 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

Под устойчивостью понимают способность конструкции сохранять первоначальную форму упругого равновесия.

Различают:

1.Устойчивое упругое равновесие, когда деформированное тело после снятия нагрузки, вызвавшей потерю устойчивости, возвращается в первоначальное состояние.

2.Неустойчивое упругое равновесие, когда деформированное тело после снятия нагрузки, вызвавшей потерю устойчивости, в первоначальное состояние не возвращается.

3.Критическое упругое состояние, когда тело находится в безразличном равновесии, то есть может

сохранить первоначальную форму, а может и потерять ее.

Нагрузка, при увеличении которой тело переходит в состоянии неустойчивого упругого равновесия, называется критической.

11.1 Вывод формулы Эйлера (определение критической силы)

Формулу Эйлера получим из приближенно-го дифференциального уравнения изогнутой оси стержня

относительно которой осевой момент инерции минимален.

Знак «+» перед MX отбрасываем, т.к. при осевом изгибе знаки второй производной прогиба и изгибающего момента всегда различны.

Тогда EImin y MX Fy

уравнение вида y k2 y 0,

(11.3)

93

Решение этого уравнения представляет собой гармоническую функцию y=A·sin kz+B·cos kz (11.5)

где А и В – постоянные интегрирования. Найдем их из граничных условий:

Здесь n – количество полуволн синусоиды на длине стержня l.

94

В полученной формуле удобнее перейти на коэффициент приведения

где μl=L – приведенная длина стержня.

В расчетах на устойчивость для обеспечения запаса устойчивости сле-

дует принимать [F] Fкр , nу

где nу – коэффициент запаса устойчивости.

Для сталей принимают nу=1,8..3, для чугуна nу=5..6,5.

11.2Область применимости формулы Эйлера

Одно из основных допущений при выводе формулы Эйлера заключается в том, что напряжения в сжимаемом стержне не превышают предела про-

Отсюда получаем область применимости формулы Эйлера

95

Например, для малоуглеродистой стали (Ст.3), нижний предел приме-

Верхний предел из практических соображений принимают λ=200. Изобразим уравнения σкр графически на координатной сетке с осями

σкр – λ для малоуглеродистой стали.

На участке λпред ≤ λ ≤ 200 критическое напряжение вычисляем по формуле (10.10).

На участке λ ≤ 35 стержень имеет малую гибкость и расчет на устойчивость не проводится, здесь принимают σкр= σт.

96

На участке 35 ≤ λ ≤ λпред теоретические вычисления σкр чрезвычайно сложны, поэтому в расчетах используют формулу Ясинского:

кр a b с 2 .

Значения коэффициентов a, b и c приведены в справочниках, например в [1]. Для пластичных материалов коэффициент c=0.

Следует отметить, что неправильный выбор формул σкр при расчетах на устойчивость может привести к опасным последствиям.

11.3 Коэффициент снижения допускаемого напряжения на устойчивость

Потеря устойчивости сжатых стержней происходит, как правило, раньше, чем потеря прочности, то есть σкр<σт.

Расчеты на устойчивость всегда следует проводить с запасом устойчи-

вости при допускаемом напряжении на устойчивость [ ]у кр , то есть так nу

же, как и расчеты на прочность проводят с запасом прочности при допускае-

мом напряжении на сжатие [ ]c т . n

Значения коэффициентов φ даны в таблицах, например [1].

С учетом коэффициента φ условие устойчивости имеет вид

N [ ]с .

A

97

11.3.1Расчеты на устойчивость

(порядок расчета)

Проверочный расчет

1.Определяем гибкость стержня l .

imin

2.По таблицам φ=f(λ) находим значения φ и вычисляем допускаемое напряжение на устойчивость [ ]у [ ]с .

3.Сравниваем фактическое напряжение в сжатом стержне с допус-

4.По таблицам находим коэффициент 1 f ( 1). Если

98

12РАСЧЕТ КРИВЫХ СТЕРЖНЕЙ

Винженерной практике зачастую необходимо производить расчеты кривых стержней: арок, звеньев цепей, крюков и пр.

Кривыми называют стержни, имеющие криволинейную ось.

Впоперечном сечении плоских кривых стержней в общем случае возникает 3 внутренних силовых фактора: продольная сила N, поперечная сила Q и изгибающий момент MX.

12.1Построение эпюр N, Q и MX для кривых стержней

Для кривых стержней эпюры удобно строить в полярных координатах, следовательно, внутренние силовые факторы должны быть выражены как функция от угла φ.

Продольная сила N равна сумме всех сил, расположенных по одну сторону от сечения и спроецированных на касательную к оси стержня, проведенную в рассматриваемом сечении.

Поперечная сила Q равна сумме всех сил, расположенных по одну сторону от сечения и спроецированных на нормаль к оси стержня, проведенную в рассматриваемом сечении.

Изгибающий момент MX равен сумме всех моментов (образованных внешними усилиями), расположенных по одну сторону от сечения относительно его центра тяжести.

Правило знаков:

Продольная сила N считается положительной, если она вызывает растяжение и наоборот.

Поперечная сила Q считается положительной, если она стремится повернуть стержень относительно сечения по часовой стрелке и наоборот.

Изгибающий момент MX считают положительным, если он увеличивает кривизну стержня и наоборот.

Если повернуть положительную продольную силу N на 900 по часовой стрелке, получим положительное направление поперечной силы Q.

Положительные эпюры откладываем внутрь контура кривого

стержня, а отрицательные наружу.

Штриховку эпюр делаем в радиальном направлении.

Построим эпюры внутренних усилий для данного кривого стержня.

99

Пусть на конце кривого стержня радиусом R приложены вертикальная сила 2F и горизонтальная сила F.

Составим выражения внутренних усилий в произвольном сечении стержня на координате φ, а для удобства проецирования внешних усилий на нормаль и касательную, разместим их в сечении на координате φ:

N=-NF - N2F=-F·cos φ - 2F·sin φ =-F(2sin φ + cos φ); Q=-QF+Q2F=-F·sin φ + 2F·cos φ =F(2cos φ - sin φ);

MX=2F·h2F - F·hF=2FR·sin φ - F(R-Rcos φ)=FR(2sin φ + cos φ - 1).

Для определения экстремального значения MX найдем соответствующую этому значению координату φ из условия:

Q 0 2sin sin 0 tg 2 63026 .

При построении эпюр удобно текущие значения N, Q и MX сводить в таблицу:

По полученным значениям строим эпюры N, Q и MX.

100