Задача 1

Дано: напряжение фазы А – u_A = 170Sinωt + 113Sin(3ωt + 30º) + 70,7Sin(5ωt - 45º) B, сопротивления в фазах потребителя первой гармоники – Z_A = 25 Ом, Z_В = -j30 Ом, Z_С = j18 Ом, схема на рис. 1.

Определить:

1. При замкнутом и разомкнутом рубильнике показания ваттметров, показание вольтметра на зажимах рубильника, показание амперметра в нулевом проводе и амперметра А₁ включенного в линейный провод.

2. При замкнутом рубильнике мгновенное значение линейного напряжения u_СА и тока в фазе В i_В. Мгновенное значение тока в нулевом проводе i_N.

Решение:

Заданное напряжение u_A имеет три гармонические составляющие – прямой, нулевой и обратной последовательностей. Запишем мгновенные значения фазных напряжений

u_A = 170Sinωt + 113Sin(3ωt + 30º) + 70,7Sin(5ωt - 45º),

u_B = 170Sin(ωt - 120º) + 113Sin(3ωt + 30º) + 70,7Sin(5ωt + 75º),

u_C = 170Sin(ωt + 120º) + 113Sin(3ωt + 30º)+ 70,7Sin(5ωt - 165º).

Дальнейшие вычисления ведем для каждой гармонической составляющей отдельно.

Ключ Р замкнут.

Расчет цепи под действием трехфазного напряжения первой гармоники.

Сопротивления фаз первой гармоники

Z_A1 = 25 Ом, Z_В1 = -j30 Ом, Z_С1 = j18 Ом.

Комплексные действующие значения фазных напряжений первой гармоники

U_A1 = = 120,57 B, U_B1 = B, U_C1 = B.

Расчет фазных токов трехфазного потребителя соединенного звездой, подключенного к симметричной трехфазной сети прямой последовательности ведется по закону Ома

I_A1 = = 4,8228 A;

I_В1 = =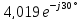A,

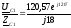I_C1 = = A.

Для расчета тока нейтрального провода применяем первый закон Кирхгофа.

I_N1 = I_A1 + I_В1 + I_C1 = 4,82 + 4,019Cos(-30°) + j4,019Sin(-30°) + 6,69Cos30° +j6,69Sin30° = 14,1 + j1,33 =

Линейное напряжение между фазами А и В можно определить как разность напряжений этих фаз

U_AB1 = U_A1 - U_B1 = 120,57-120,57Cos(-120°)+j120,57Sin(-120°)=180,9+j104,4=.

Расчет цепи под действием трехфазного напряжения третьей гармоники.

Сопротивления фаз третьей гармоники

Z_A3 =25 Ом, Z_В3 = -j10 Ом, Z_С3 = j54 Ом.

Комплексные действующие значения фазных напряжений третьей гармоники

U_A3 = 80,14e^j30º B, U_B3 = 80,14e^j30º B, U_C1 = 80,14e^j30º B.

Расчет фазных токов трехфазного потребителя соединенного звездой, подключенного к симметричной трехфазной сети нулевой последовательности ведется по закону Ома

I_A3 = =A;

I_В3 = = A,

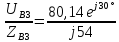I_C3 = = A.

Для расчета тока нейтрального провода применяем первый закон Кирхгофа.

I_N3 = I_A3 + I_В3 + I_C3 = + j3,2Sin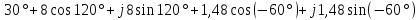 = -0,48872+j7,246486==A.

Линейное напряжение между фазами А и В третьей гармоники

U_AB3 = U_A3 - U_B3 = 0.

Расчет цепи под действием трехфазного напряжения пятой гармоники.

Сопротивления фаз пятой гармоники

Z_A5 = 25 Ом, Z_В5 = -j6 Ом, Z_С5 = j90 Ом.

Комплексные действующие значения фазных напряжений пятой гармоники

U_A5 = 50,14e^-j45º B, U_B5 = 50,14e^j75ºB, U_C5 = 50,14e^-j165ºB.

Расчет фазных токов трехфазного потребителя соединенного звездой, подключенного к симметричной трехфазной сети обратной последовательности ведется по закону Ома

I_A5 = 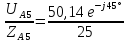= 2e^-j45º A;

I_В5 = = A,

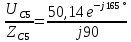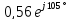I_C5 = = A.

Для расчета тока нейтрального провода применяем первый закон Кирхгофа.

I_N5 = I_A5 + I_В5 + I_C5 = A.

Линейное напряжение между фазами А и В можно определить как разность напряжений этих фаз

U_AB5 = U_A5 - U_B5 = B.

Показание амперметра в нейтральном проводе А₀

= А.

Показание амперметра в фазе А₁

= =6,124 А.

Показание вольтметра при замкнутом ключе составит ноль.

Показания ваттметров

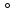P₁ =U_А1I_N1 cos(φ_A1 + 180) + U_А3I_N3 cos(φ_A3 + 180) + U_А5I_N5 cos(φ_A5 + 180) = 120,57cos175 + 80,147,26cos116 + 50,146,927cos(-154) = 1700+255+320=2275Вт,

P₂ =U_АB1I_N1 cos(φ_АB1) + U_АB3I_N3 cos(φ_АB3) + U_АB5I_N5cos(φ_АB5) = 208,814,16cos(30 - 5) + 87,246,927cos(115) = 2425,4 Вт.

Запишем мгновенное значение тока в фазе В

i_B(t) = 5,684Sin(ωt - 30) + 11,315Sin(3ωt +120) + 11,823Sin(5ωt + 165) A.

Мгновенное значение линейного напряжения

u_АB (t) = 295,288Sin(ωt + 30) + 122,81Sin(3ωt - 75) B.

Мгновенное значение тока в нейтральном проводе

i_N(t) = 20,022Sin(ωt + 5) + 10,267Sin(3ωt + 94) + 9,796Sin(5ωt + 169) A.

Ключ разомкнут.

Расчет цепи под действием трехфазного напряжения первой гармоники.

В трехпроводной трехфазной цепи, соединенной звездой, между нейтральными точками возникает напряжение смещения. Напряжение смещения рассчитывается методом двух узлов

Запишем закон Ома для расчета токов в фазах с учетом напряжения смещения

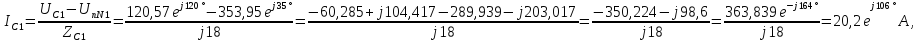
Расчет цепи под действием трехфазного напряжения третьей гармоники.

Токи в фазах трехпроводной трехфазной цепи, соединенной звездой, не содержат гармоник кратных трем. Напряжение смещения нейтрали равно фазному напряжению

U_nN3 = U_ф3 =80,14е^j30º B.

Расчет цепи под действием трехфазного напряжения пятой гармоники.

Из расчета цепи при разомкнутом ключе запишем показания приборов.

Показания амперметра в нейтральном проводе, а также первого и второго ваттметров, составят ноль.

Показание амперметра в фазе А

=11,427 А.

Показание вольтметра между нейтральными точками

=365,45 В