
Tema_4
.docxТема 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРОВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ.
1) Закон движения материальной точки в вязкой среде определяется соотношениями х=0,2е-0,5t sin(πt), y=0.4e-0.5t sin(πt)+1, z=0 (координаты заданы в метрах, время t - в секундах). Определить модуль равнодействующей сил, действующих на точку, если ее масса m = 2 г.
Движение материальной точки в проекциях на оси координат:
m = Fx
, m
= Fx
, m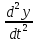 = Fy
= Fy
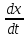 =
=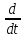 0,2е-0,5t
sin(πt)=0.2
0,2е-0,5t
sin(πt)=0.2
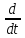 е-0,5t
sin(πt)
={
е-0,5t
sin(πt)
={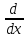 (uv)=
(uv)=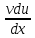 +
+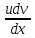 }=0.2(е-0,5t
(-0.5)sin(πt)
+ е-0,5t
πcos(πt)=
}=0.2(е-0,5t
(-0.5)sin(πt)
+ е-0,5t
πcos(πt)=
=е-0,5t[ 0.2cos(πt)-0.1sin(πt)] = Vx
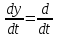 0,4е-0,5t
sin(πt)+1=0.4
0,4е-0,5t
sin(πt)+1=0.4
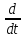 е-0,5t
sin(πt)
+
е-0,5t
sin(πt)
+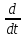 1
={
1
={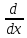 (uv)=
(uv)=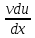 +
+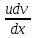 }=0.4(е-0,5t
(-0.5)sin(πt)
+ е-0,5t
πcos(πt)=
}=0.4(е-0,5t
(-0.5)sin(πt)
+ е-0,5t
πcos(πt)=
=е-0,5t [0.4cos(πt)-0.2sin(πt)] = Vy
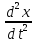 =
=
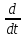 е-0,5t
[0.2cos(πt)-0.1sin(πt)]
={
е-0,5t
[0.2cos(πt)-0.1sin(πt)]
={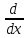 (uv)=
(uv)=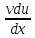 +
+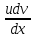 }=
е-0,5t
[(-0.5)(0.2πcos(πt)-0.1sin(πt)
+ (-0.2π2sin(πt))-
}=
е-0,5t
[(-0.5)(0.2πcos(πt)-0.1sin(πt)
+ (-0.2π2sin(πt))-
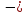 0.1πcos(πt)]=
е-0,5t
[0.05sin(πt)
- 0.2π2sin(πt)
- 0.2πcos(πt)]
= е-0,5t
[(0.05-
0.2π2)sin(πt)
-
0.2πcos(πt)]
0.1πcos(πt)]=
е-0,5t
[0.05sin(πt)
- 0.2π2sin(πt)
- 0.2πcos(πt)]
= е-0,5t
[(0.05-
0.2π2)sin(πt)
-
0.2πcos(πt)]
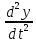 =
=
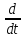 е-0,5t
[0.4cos(πt)-0.2sin(πt)]
={
е-0,5t
[0.4cos(πt)-0.2sin(πt)]
={ (uv)=
(uv)=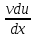 +
+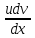 }=
е-0,5t
[(-0.5)(0.4πcos(πt)-0.2sin(πt)
+ (-0.4π2sin(πt))-
}=
е-0,5t
[(-0.5)(0.4πcos(πt)-0.2sin(πt)
+ (-0.4π2sin(πt))-
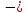 0.2πcos(πt)]=
е-0,5t
[0.1sin(πt)
- 0.4π2sin(πt)
- 0.4πcos(πt)]
= е-0,5t
[(0.1
- 0.4π2)sin(πt)
-
0.4πcos(πt)]
0.2πcos(πt)]=
е-0,5t
[0.1sin(πt)
- 0.4π2sin(πt)
- 0.4πcos(πt)]
= е-0,5t
[(0.1
- 0.4π2)sin(πt)
-
0.4πcos(πt)]
F
=
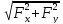
Ответ: F = 8.944*10-4 е-0,5t [(0.25 - π2)sin(πt) - πcos(πt)]
2) Тяжелое тело,
брошенное вверх под углом 60о
к горизонту
с начальной скоростью 20
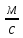 .
Пренебрегая сопротивлением воздуха,
определить высоту траектории h
и скорости тела vh
на ее вершине. Какую скорость тело будет
иметь через 2 секунды после броска?
.
Пренебрегая сопротивлением воздуха,
определить высоту траектории h
и скорости тела vh
на ее вершине. Какую скорость тело будет
иметь через 2 секунды после броска?
В полете на тело брошенное под углом действует только сила тяжести Р̅. Поэтому дифференциальное уравнение принимает вид :
m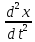 =0
, m
=0
, m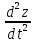 =-P̅
↔
=-P̅
↔
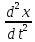 =0
,
=0
,
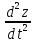 =-g
=-g
Проинтегрируем по времени записанные уравнения получим:
∫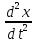 = ∫0dt
, ∫
= ∫0dt
, ∫
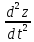 = -∫gdt
= -∫gdt
В результате имеем проекции вектора скорости снаряда на оси координат:
Vx= C1, Vz = -gt + C2
Интегрируем полученные выражения ещё раз, тем самым определим координаты снаряда как функцию времени
∫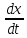 = ∫C1
dt
→ x
= C1t
+ C4
, ∫
= ∫C1
dt
→ x
= C1t
+ C4
, ∫
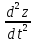 = -∫gdt
+ ∫C2dt
→
z
= -
= -∫gdt
+ ∫C2dt
→
z
= -
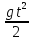 + C2t
+ C4
+ C2t
+ C4
Для определение С1, С2, С3, С4 полагаем что x0 = z0 = 0 , при t = 0 отсюда найдем проекции начальной скорости:
V0x
= V0
cos
α
= C1
= 10
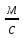 ,
V0z
= V0
sin
α
= C2
= 17.32 , С3
= С4
= 0
,
V0z
= V0
sin
α
= C2
= 17.32 , С3
= С4
= 0
Теперь можно написать записать уравнение движение тела:
x
= 10t
z
= -
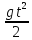 + 17.32t
+ 17.32t
Найдем время при
Vz
= 0 (т.е. на наивысшей точке) t
=
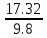 = 1.767 c.
Подставим это значение z
= -
= 1.767 c.
Подставим это значение z
= -
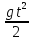 + 17.32t
получим высоту наивысшей точки:
+ 17.32t
получим высоту наивысшей точки:
h = 4.9 * (1.767)2 + 17.32*1.767 =15.305м.
Vx(2)
= 10
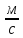 .
Vz(2)
= -9.8*2 + 17.32 = -2,28
.
Vz(2)
= -9.8*2 + 17.32 = -2,28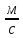 , V(2) =
, V(2) =
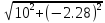 =10.256
=10.256
Ответ:
На вершине траектории при Vz
= 0, Vh=
Vx
= 10
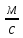 , h
= 15.305м,
V(2)
= 10.256
, h
= 15.305м,
V(2)
= 10.256
3)
На участке b0b1
тяжёлое тело скользит по наклонной
шероховатой плоскости и далее свободно
падает на горизонтальную поверхность,
касаясь ее в положении b2
(рис 2). Определить коэффициент трения
f
наклонной плоскости, если b0b1
= S
= 2м, L
= 1м , H
= 2м, α
= 30o.
Скорость v0
тела в положении b0
равна 3
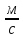 .
.
