
Tema_5
.docxТема 5. ВЕКТОРНАЯ ТЕОРЕМА ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ.
 1)
Шарик , подвешенный на нити длинной 30
см , движется по окружности , образуя
конический маятник . определить натяжении
нити Т и
скорость шарика v
, если нить составляет с веревкой угол
600 , а вес шарика 1 Н. Использовать
изображенную на рисунке систему
координат.
1)
Шарик , подвешенный на нити длинной 30
см , движется по окружности , образуя
конический маятник . определить натяжении
нити Т и
скорость шарика v
, если нить составляет с веревкой угол
600 , а вес шарика 1 Н. Использовать
изображенную на рисунке систему
координат.
|
Построим подвижную естественную систему координат. По принципу Даламбера записываем : Р̅ + Т̅ + Ф̅ῖ + Ф̅п = 0 Ф̅ῖ
=
Составим дифференциальные уравнения движения точки в подвижной естественной системе координат: m
|
y
Фп Т̅ Фῖ
x
Р̅
V̅
(т.к. шари движется по одной плоскости)
Из системы уравнений находим:
V
= const ; T =
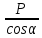 = 2 H; v =
= 2 H; v =
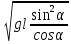 = 2.1
= 2.1
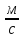 .
.
2) Тяжёлое
тело брошенное под углом 300 к
горизонту со скоростью v
= 20
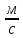 .Определить его скорость через 2 секунды
полета.
.Определить его скорость через 2 секунды
полета.
В полете на тело действует лишь одна постоянная сила - сила тяжести F̅T соответственно проекции начальной скорости на оси равны:
ox:
| V0x
= V0
cosα = 17.32
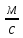
oy:
| V0y
= V0 sinα
= 10
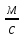
Уравнение изменения скорости по времени
записывается в виде:
Vx
= { Vx
– const }= 17.32
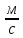 ;
;
Vy
= V0y
– gt = -9.6
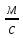
Ответ:
Vt=2
=
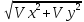 = 19.8
= 19.8
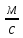
3) Материальная точка массой 10 грамм движется в плоскости oxy под действием силы F̅ согласно уравнениям x = t, y = t2 + 1 (координаты заданы в метрах, время t - в секундах). Требуется :
-
Определить момент l0 вектора количества движение точки относительно начала координат и двумя способами вычислить модуль вектора при t = 0
-
Определить момент силы F̅ относительно начала координат ;
-
Двумя способами вычислить модуль вектора M0(F̅) при t = 0 и t = 1с.
-
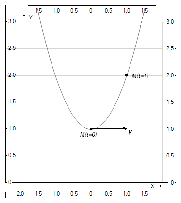
В данном законе движения траектория точки будет парабола с вершиной М(0;1)
Радиус вектора находим по формуле: r̅(t) = xi̅ + yj̅ = ti̅ +(t2+1)j̅
Найдём
количество движение материальной точки:
mv̅(t)=m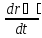 = i̅
+2tj̅
тогда, момент
l0
вектора количества
движение точки:
= i̅
+2tj̅
тогда, момент
l0
вектора количества
движение точки:
l0
= r̅
⨯ mv̅
= k̅
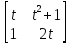 m
= k̅m(2t2
–(t2+1))
=m(t2-1)k̅
m
= k̅m(2t2
–(t2+1))
=m(t2-1)k̅
Другой способ определения l0 ; ведь он есть вектор который определяется построением траектории и отмечаем на ней положение точки в момент времени t=0;
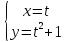
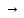 y=x2+1
M(t=0)(0;1)
y=x2+1
M(t=0)(0;1)
Далее определяется скорость и строем вектор скорости:
V̅x
= =1; V̅y
=
=1; V̅y
=
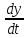 = 2t V0=
1
= 2t V0=
1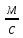 При известной скорости модуль вектора
mv̅
определить легко. Плечо h
вектора mv̅
относительно начала координат определим
по рисунку. Теперь:
При известной скорости модуль вектора
mv̅
определить легко. Плечо h
вектора mv̅
относительно начала координат определим
по рисунку. Теперь:
l0
(0) = mvh
=10г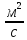
б) По теореме изменений момента количества движений материальной точки:
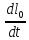 = M0(F)
= 2mtk̅
= M0(F)
= 2mtk̅
в) В произвольный момент времени имеем:
M0(F)
= r̅(t)
⨯
F̅
= i̅
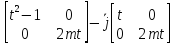 +k̅
+k̅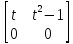 = 2mt(t2+1)-2mt2=
2m(t3+t-t2)
= 2mt(t2+1)-2mt2=
2m(t3+t-t2)
M0 t=0
= 0: M0
t=0
= 0: M0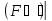 t=1=2*0.01*1=0.02
H·м
t=1=2*0.01*1=0.02
H·м
Изображаем силу в положении точки t=0, t=1. Находим плечи h1 и h2 затем подставляем:
M0 t=0
= Fh1
=
2*0.01*0*1=0 , M0
t=0
= Fh1
=
2*0.01*0*1=0 , M0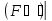 t=1
= Fh2=2*0.01*1*1=0.02
H·м
t=1
= Fh2=2*0.01*1*1=0.02
H·м

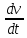 ; Ф̅п =
; Ф̅п =
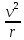 =
=
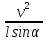
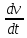 = 0; m
= 0; m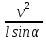 = Tsinα ; P = Tcosα
= Tsinα ; P = Tcosα