2.1.3. Определение коэффициента теплоотдачи при кипении

При пузырьковом кипении жидкостей коэффициент теплоотдачи находится по следующим зависимостям [5]:

• при кипении на поверхности нагрева, погруженной в большой объем жидкости [1],

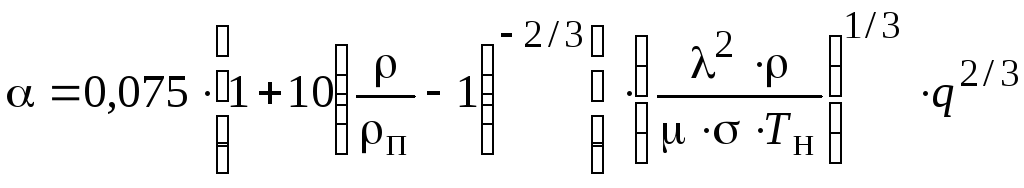; (2.45)

• при кипении в трубах [1]

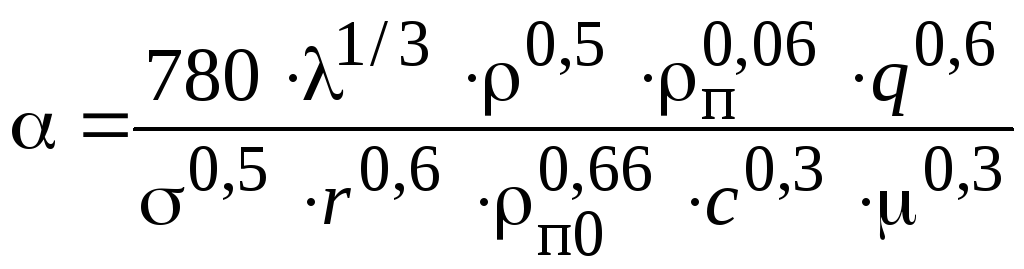, (2.46)

где - температура насыщения (кипения), К; плотность пара, кг/м³;  плотность пара при нормальных условиях, кг/м³; r  удельная теплота испарения, Дж/кг;   коэффициент поверхностного натяжения жидкости, Н/м; q  удельная тепловая нагрузка, Вт/м².

Критическая тепловая нагрузка , при которой пузырьковое кипение переходит в пленочное, определяется по уравнению [6], Вт/м²,

. (2.47)

В формулах (2.45)(2.47) физико-химические параметры жидкости определяются при температуре насыщения (кипения).

2.1.4. Кипение в большом объеме на горизонтальном пучке

оребренных труб

При кипении хладонов на пучках из труб с накатными ребрами, без примесей масла коэффициент теплоотдачи определяется по уравнению [8], Вт/(м²К),

, (2.48)

где  коэффициент, учитывающий влияние числа рядов по высоте пучка. Его значение может быть определено по графикам на рис. 2.3. При условии: , поправочный коэффициент .

средний коэффициент теплоотдачи эталонного (шестирядного) пучка, Вт/(м²К) (см. формулы (2.49)2.50)).

Это значение может быть найдено по следующим уравнениям [8, 9]:

• для R134A

; (2.49)

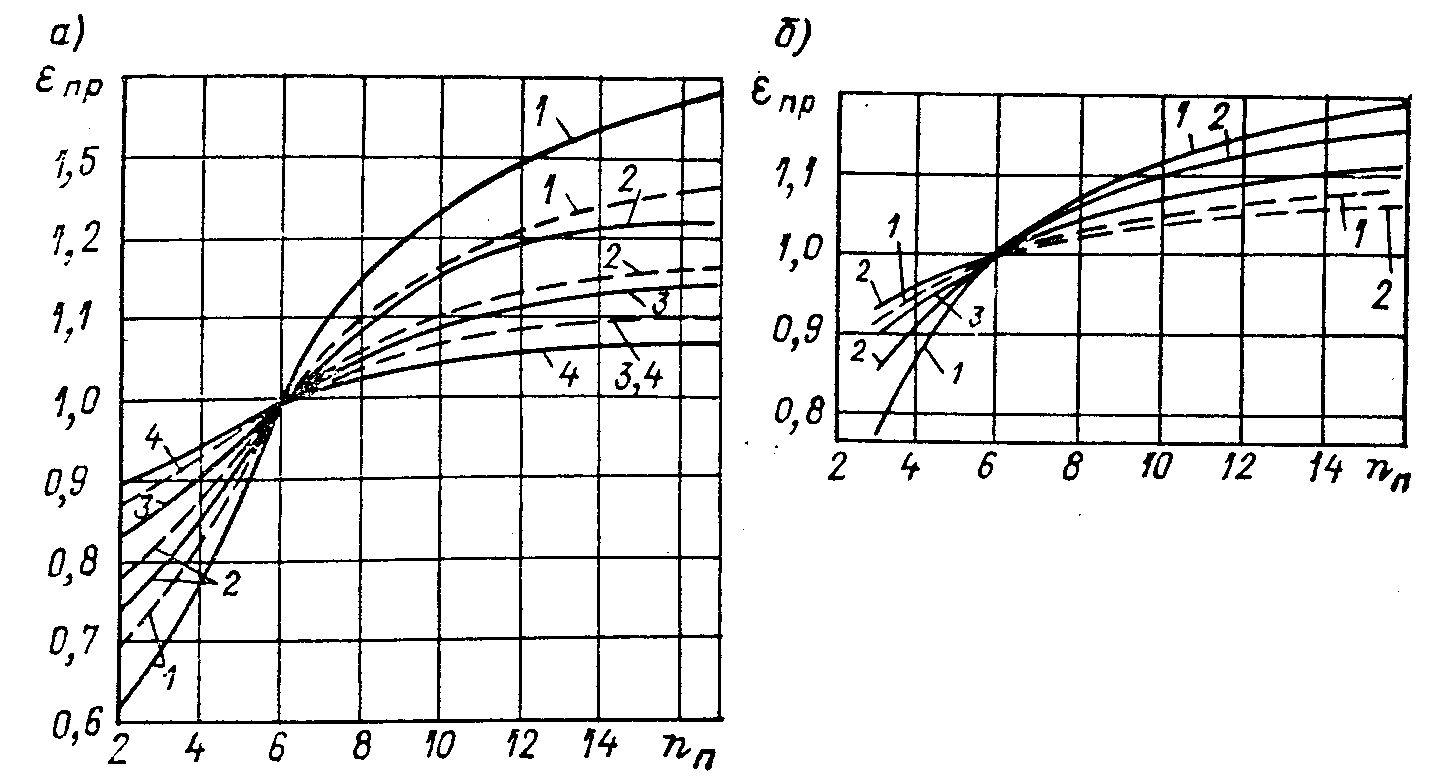
Рис.2.3. Поправочный множитель , учитывающий влияние числа

рядов в пучке оребренных труб

а) для R134A;

б) для R22

1  500 Вт/м²; 2  1000 Вт/м²; 3  2000 Вт/м²;

4  3000 Вт/м²

С; С

• для R22

, (2.50)

где  давление холодильного агента в межтрубном пространстве, бар (1 бар = 10⁵ Па);  разность температуры кипения фреона и температуры стенки трубы, С.

Уравнения для справедливы при следующих условиях:

• пучок шестирядный, с геометрическими размерами ;

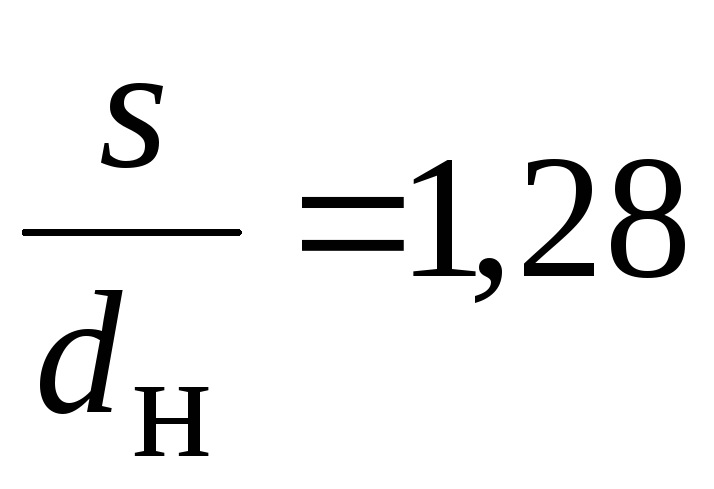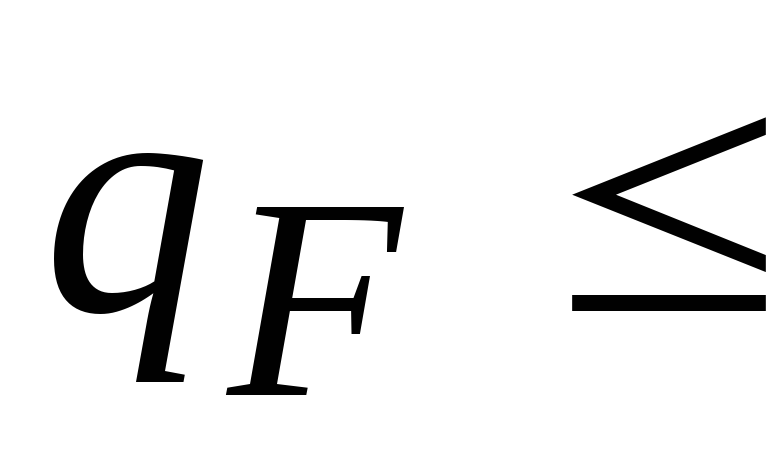• 7000 Вт/м².

После определения коэффициента теплопередачи K рассчитывается площадь поверхности теплообмена , м²:

.

Далее проводится сопоставление расчетного значения со значением площади теплообмена нормализованного теплообменника.

Если выполняется условие

или , (2.51)

тогда тепловой расчет теплообменника заканчивается. В противном случае необходимо выбрать другой вариант теплообменного аппарата и расчет повторить.

2. Гидравлический расчет теплообменных аппаратов [6]

При перемещении теплоносителя через теплообменник следует затратить определенную мощность на преодоление гидравлического сопротивления. Гидравлический расчет аппарата сводится в общем случае к определению потерь давления в общем случае по тракту каждого теплоносителя. Потери давления складываются из потерь по длине и потерь на преодоление местных сопротивлений

, (2.52)

где  гидравлическое сопротивление по длине канала, Па;  местные потери давления, Па.

, (2.53)

где L  длина канала, м;  коэффициент гидравлического сопротивления по длине; _м  коэффициент местного сопротивления (табл. 2.9); w  скорость теплоносителя в канале, м/с.

Таблица 2.9. Значения коэффициентов местных сопротивлений

№ п/п	Местные сопротивления	
1	Входная и выходная камеры (удар и поворот)	1,5
2	Поворот между ходами или секциями на 180	2,5
3	Вход в трубы и выход из них	1,0
4	Вход в межтрубное пространство и выход из него	1,0
5	Поворот через сегментную перегородку	1,5
6	Поворот на 180 через колено в секционных теплообменниках	2,0
7	Поворот в Uобразной трубке	0,5
8	Огибание перегородок, поддерживающих трубки	0,5
9	Сопротивление пучка труб	3

Коэффициент гидравлического сопротивления определяется по следующим уравнениям:

• при ,

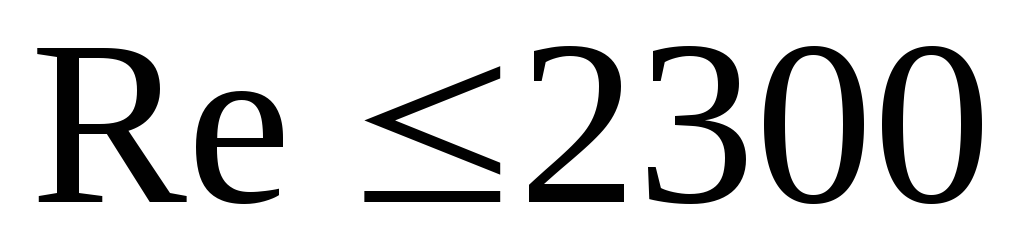, (2.54)

где А  коэффициент, зависящий от формы канала (табл. 2.10);

• при ,

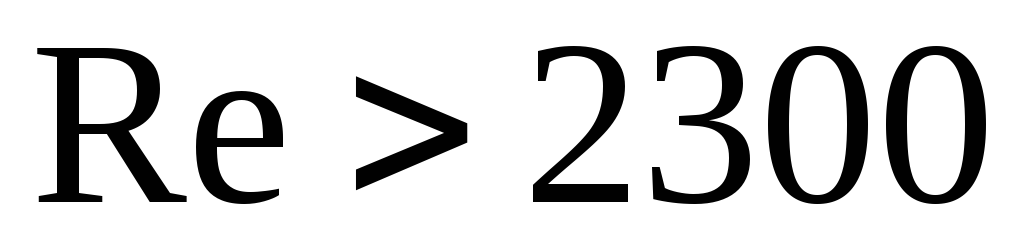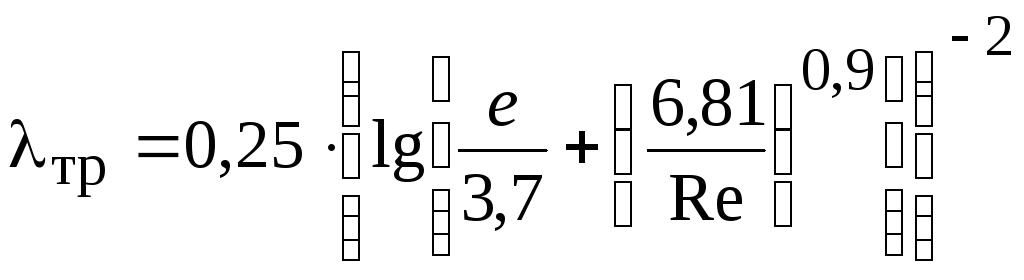, (2.55)

где  относительная шероховатость труб;   высота выступов шероховатостей, м (табл. 2.11).

Таблица 2.10. Значение коэффициента A в уравнении (2.54)

№ п/п	Форма сечения	А
1	Круг диаметром а	64	а
2	Квадрат стороной а	57	а
3	Кольцо шириной а	96	2а
4	Прямоугольник высотой а и шириной :	96 85 73 62	2а 1,81а 1,6а 1,3а

Таблица 2.11. Ориентировочные значения шероховатости труб  [6]

№ п/п	Трубы	, мм
1	Стальные новые	0,06 – 0,1
2	Стальные, бывшие в эксплуатации, с незначительной коррозией	0,1 – 0,2
3	Стальные старые, загрязненные	0,5 – 1
4	Чугунные новые, керамические	0,35 – 1
5	Алюминиевые гладкие	0,015 – 0,06
6	Трубы из латуни, меди	0,0015 – 0,01

В общем случае для трубного пространства теплообменника гидравлическое сопротивление , Па, определяется по уравнению

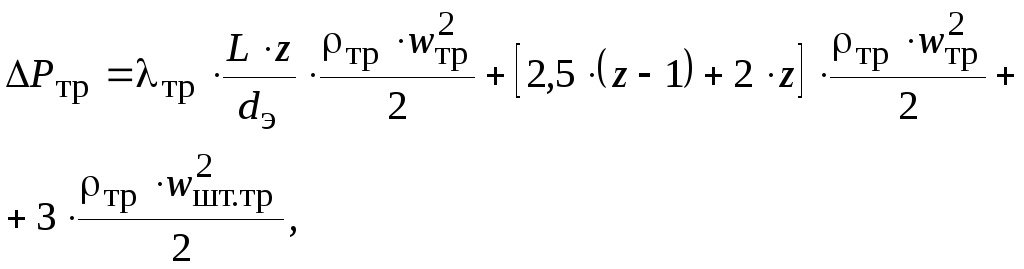(2.56)

где z  число ходов в трубном пространстве;  скорость теплоносителей в штуцерах трубного пространства, м/с;  плотность жидкости в трубном пространстве, кг/м³;  скорость жидкости в трубах, м/с.

Для межтрубного пространства гидравлическое сопротивление в общем случае рассчитывается по выражению, Па

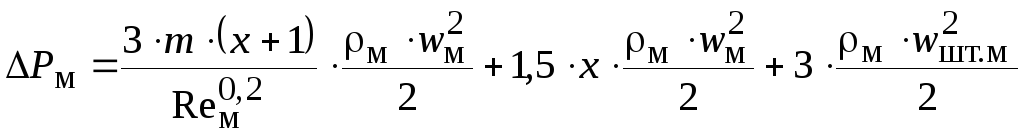, (2.57)

где - число Рейнольдса в межтрубном пространстве,; скорость теплоносителей в штуцерах трубного пространства, м/с; , соответственно, плотность, кг/м³, и кинематическая вязкость, м²/с, теплоносителя, протекающего в межтрубном пространстве; x  число сегментных перегородок; m  число рядов труб, преодолеваемых потоком теплоносителя в межтрубном пространстве

. (2.58)

Для пластинчатых теплообменников:

, (2.59)

где L  приведенная длина каналов, м; x  число пакетов для данного теплоносителя; - скорость теплоносителя при течении между пластинами и в штуцерах, соответственно, м/с.

При поперечном обтекании пучка гладких труб находится из следующей зависимости [1]:

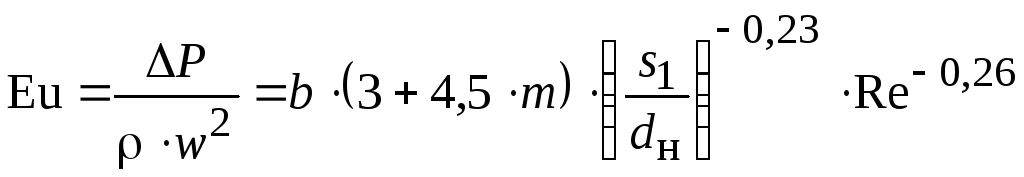. (2.60)

Для шахматных пучков:

• при ,

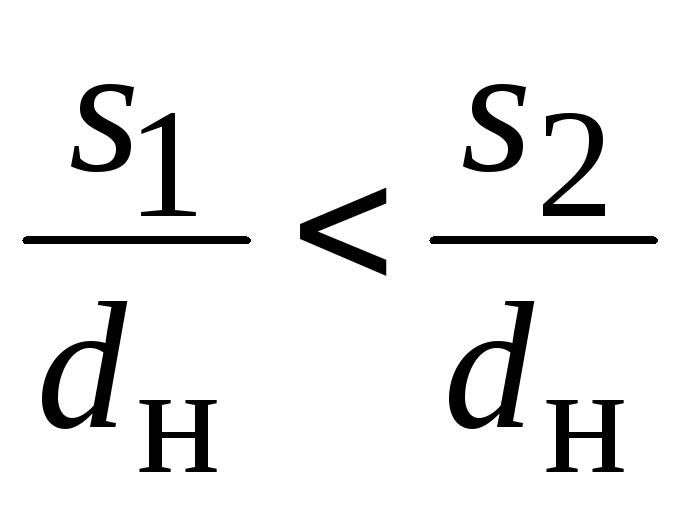; (2.61)

• при ,

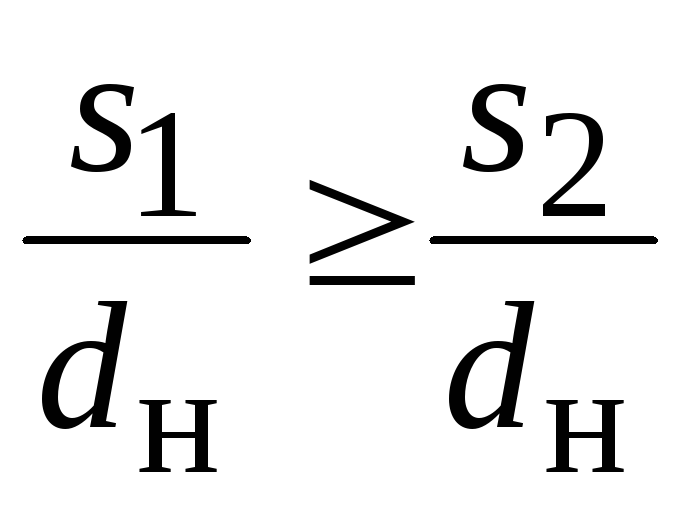, (2.62)

где b  поправочный коэффициент, зависящий от угла атаки  (табл. 2.11); m  число рядов труб в пучке в направлении движения потока;  поперечный и продольный шаги, м.

Таблица 2.11. Значения коэффициента b в уравнениях (2.60)  (2.61)

	90	80	70	60	50	40	30	20	10
B	1	1	0,95	0,83	0,69	0,53	0,38	0,27	0,15

Гидравлическое сопротивление пучков труб с кольцевыми, квадратными и поперечно-спиральными ребрами может быть рассчитано по приведенным ниже уравнениям [4].

Для шахматных пучков:

• при

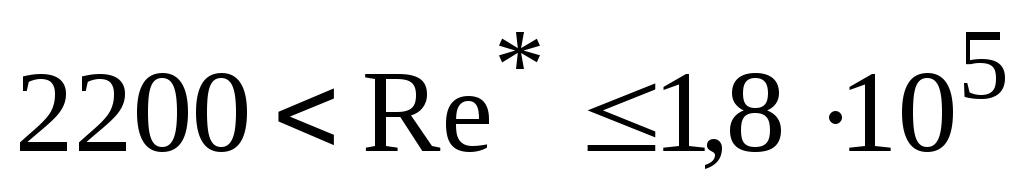
; (2.63)

• при

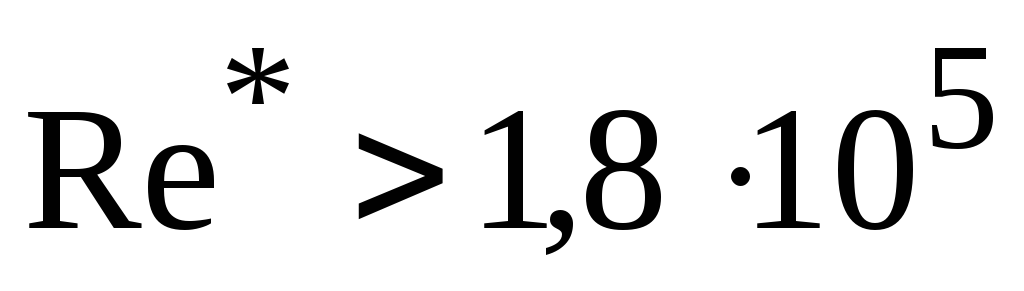
, (2.64)

где  число Рейнольдса, ; эквивалентный диаметр канала, м;  относительный диаметр, м,

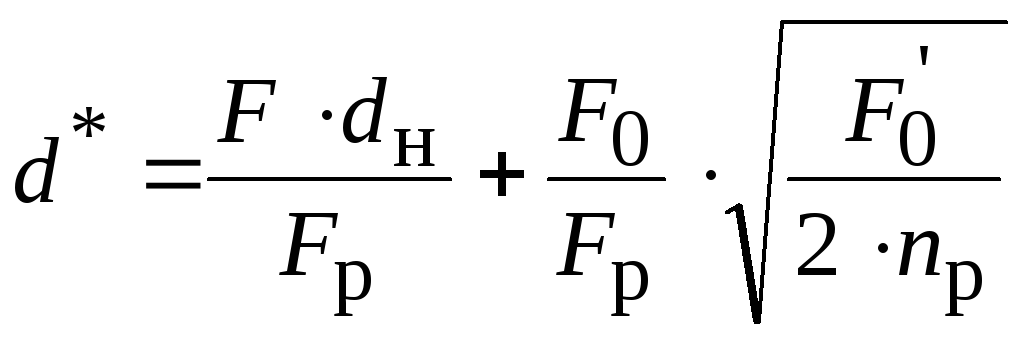, (2.65)

где F  площадь поверхности неоребренной трубы длиной 1 м, м²/м; F₀  площадь поверхности ребер, м²/м; F_р  общая поверхность ребристой трубы длиной 1, м²/м;  площадь поверхности ребер (без торцевых участков), м²/м;  число ребер на трубе длиной 1 м; - коэффициент, учитывающий число рядов труб в шахматном пучке:

; (2.66)

где  коэффициент, определяющий изменение перепада давления в зависимости от номера ряда (табл. 2.12).

Таблица 2.12. Значения коэффициентов ив уравнениях

(2.63)(2.66) [6]

M			M
1	2,000	2,000	6	1,000	1,224
2	1,200	1,600	7	1,000	1,192
3	1,086	1,429	8	1,000	1,168
4	1,040	1,332	9	1,000	1,149
5	1,016	1,268	10	1,000	1,134

• При ,

;

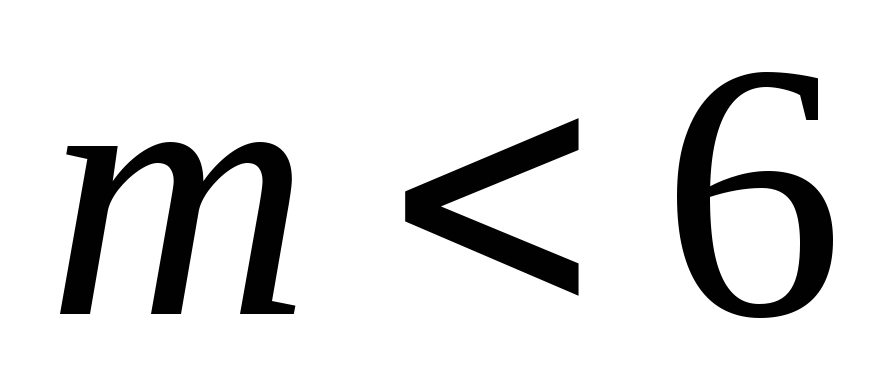• при ,

.

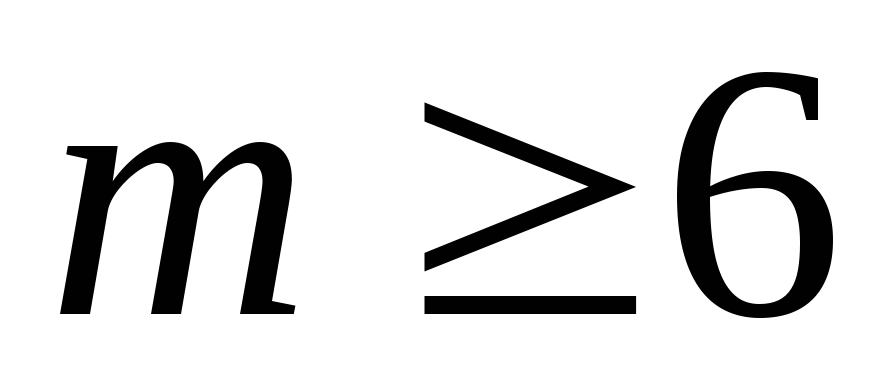Для коридорных пучков [6]:

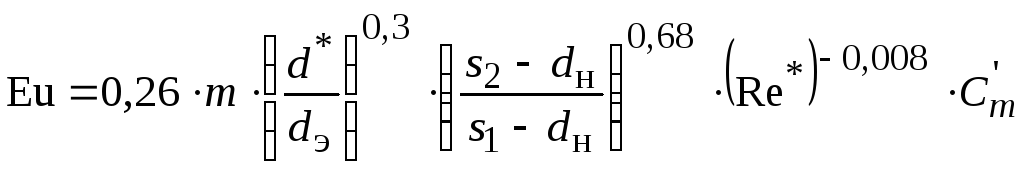, (2.67)

где  коэффициент, учитывающий число рядов труб в коридорном пучке.

; (2.68)

где - коэффициент, учитывающий влияние номера ряда труб в пучке на гидравлическое сопротивление (табл. 2.13).

Таблица 2.13. Значения коэффициентов идля коридорных

пучков [6]

M			M
1	2,750	2,750	6	1,000	1,472
2	1,600	2,176	7	1,000	1,405
3	1,287	1,879	8	1,000	1,354
4	1,140	1,694	9	1,000	1,315
5	1,056	1,567	10	1,000	1,283

• При ,

;

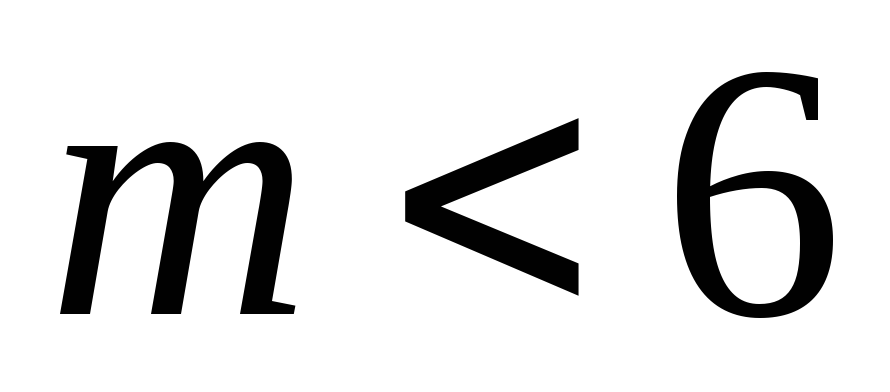• при ,

.

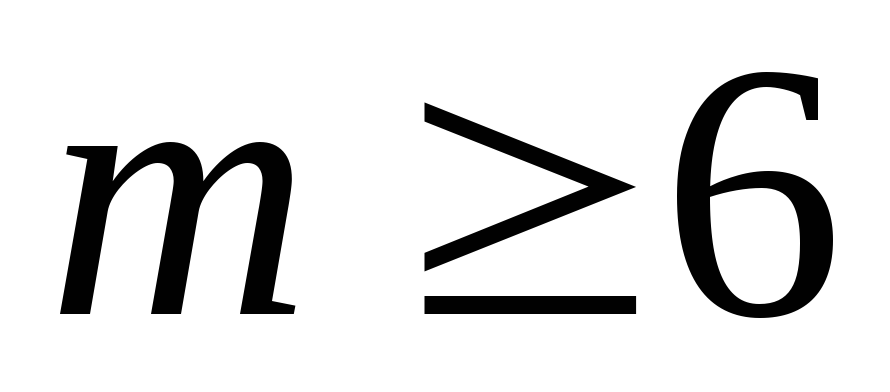Мощность N, кВт, затрачиваемая на преодоление гидравлического сопротивления, находится по выражению

, (2.69)

где  - коэффициент полезного действия нагнетательной установки (насоса, компрессора и т.п.).