
- •Утверждено
- •Оглавление
- •Введение
- •Расчет теплофизических параметров
- •2. Общая схема расчёта теплообменных аппаратов
- •2.1. Тепловой расчёт теплообменников
- •2.1.1. Определение коэффициента теплоотдачи для сред, не меняющих агрегатное состояние
- •2.1.2. Определение коэффициента теплоотдачи при конденсации паров
- •2.1.3. Определение коэффициента теплоотдачи при кипении
- •2.1.4. Кипение в большом объеме на горизонтальном пучке
- •Гидравлический расчет теплообменных аппаратов [6]
- •3. Примеры расчета теплоообменников
- •3.1. Расчет кожухотрубчатого холодильника [6]
- •3.2. Расчет пластинчатого холодильника [6]
- •3.3. Расчет пластинчатого подогревателя (конденсатора) [6]
- •448000 Вт.
- •3.4. Расчет кожухотрубчатого конденсатора [6]
- •3.5. Расчет кожухотрубчатого испарителя [6]
- •3.6. Расчет фреонового конденсатора холодильной машины
- •3.7. Тепловой расчет испарителя холодильной машины
- •4. Расчетное Задание
- •Библиографический список
- •420066, Казань, Красносельская, 51
- •420066, Казань, Красносельская, 51
2.1.1. Определение коэффициента теплоотдачи для сред, не меняющих агрегатное состояние
При течении по трубам сред, не меняющих агрегатное состояние, коэффициент теплоотдачи , Вт/(м2∙К), определяется следующими уравнениями.
Таблица 2.2. Тепловая проводимость загрязнений стенок [6]
|
№ п/п |
Среда |
|
|
1 |
Вода: загрязнённая среднего качества хорошего качества дистиллированная |
1400-1860 1860-5800 2900-5800 11600 |
|
2 |
Воздух |
2800 |
|
3 |
Нефтепродукты, масла, пары хладонов |
2900 |
|
4 |
Органические жидкости, рассолы, жидкие хладоны |
5800 |
|
5 |
Водяной пар |
5800 |
|
6 |
Пары органических жидкостей |
11600 |
Для развитого турбулентного течения при
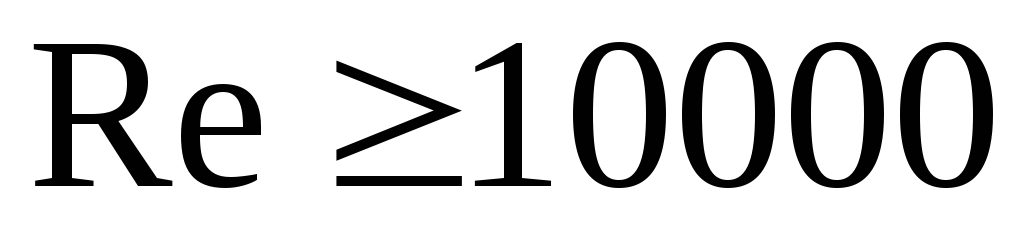 и
и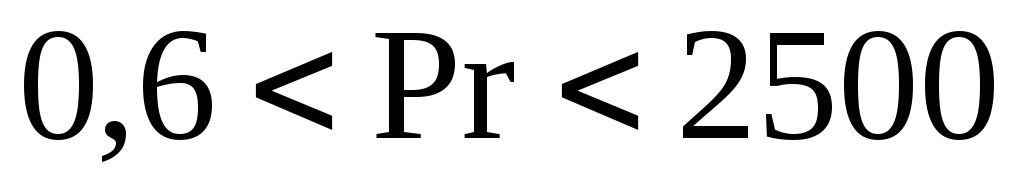 [1]
[1]
![]() ,
(2.12)
,
(2.12)
где Nu
– число Нуссельта; Re
- число Рейнольдса,
![]() ;Pr
число Прандтля,
;Pr
число Прандтля,
![]() ;
;
![]()
число Прандтля, рассчитанное при
температуре стенки; w
скорость теплоносителя, м/с;
число Прандтля, рассчитанное при
температуре стенки; w
скорость теплоносителя, м/с;
![]()
коэффициент кинематической вязкости
среды теплоносителя, м2/с;
а
и
- коэффициенты температуропроводности,
м2/с,
и теплопроводности, Вт/(мК).
теплоносителя;
коэффициент кинематической вязкости
среды теплоносителя, м2/с;
а
и
- коэффициенты температуропроводности,
м2/с,
и теплопроводности, Вт/(мК).
теплоносителя;
![]() - эквивалентный диаметр канала, м. При
течении по трубам
- эквивалентный диаметр канала, м. При
течении по трубам![]() равен внутреннему диаметру трубы. В
общем случае:
равен внутреннему диаметру трубы. В
общем случае:
![]() ,
,
где
f
площадь поперечного сечения потока,
м2;
![]() - полный смоченный периметр поперечного
сечения потока, м.
- полный смоченный периметр поперечного
сечения потока, м.
![]() поправка,
учитывающая влияние относительной
длины
поправка,
учитывающая влияние относительной
длины
![]() на теплоотдачу:
на теплоотдачу:
при
![]() ,
,![]() ;
;
при
![]() ,
,![]() ;
;
l
длина трубы,
![]() .
.
2. Для переходного
режима
![]() приближенное значение коэффициента
теплоотдачи определяется по уравнению
[3]
приближенное значение коэффициента
теплоотдачи определяется по уравнению
[3]
![]() .
(2.13)
.
(2.13)
Или может быть использовано уравнение (2.12) с введением поправки из табл. 2.3.
Таблица 2.3. Значения поправочного коэффициента для переходного
режима
|
Re |
2200 |
2300 |
2500 |
3000 |
3500 |
4000 |
5000 |
6000 |
9000 |
10000 |
|
|
0,22 |
0,35 |
0,45 |
0,59 |
0,7 |
0,76 |
0,86 |
0,91 |
0,99 |
1,0 |
3. Для ламинарного режима течения теплоносителя коэффициент теплоотдачи рассчитывается по уравнениям [3]
![]() ,
(2.14)
,
(2.14)
![]() ,
(2.15)
,
(2.15)
![]() ,
(2.16)
,
(2.16)
![]() ,
(2.17)
,
(2.17)
![]() ,
(2.18)
,
(2.18)
![]() .
(2.19)
.
(2.19)
В формулах (2.14) – (2.19):
n
= 0,11
в процессах нагрева; n
= 0,25
в процессах охлаждения; Pe
число Пекле,
![]() ;
коэффициент динамической вязкости
теплоносителя, Пас;
ст
коэффициент динамической вязкости при
температуре стенки, Пас;
Gr
число Грасгоффа,
;
коэффициент динамической вязкости
теплоносителя, Пас;
ст
коэффициент динамической вязкости при
температуре стенки, Пас;
Gr
число Грасгоффа,
![]() ;g
= 9,81 – ускорение свободного падения,
м/с2;
коэффициент объёмного расширения
теплоносителя, 1/К;
;g
= 9,81 – ускорение свободного падения,
м/с2;
коэффициент объёмного расширения
теплоносителя, 1/К;
![]()
разность температур стенки и теплоносителя,
С.
разность температур стенки и теплоносителя,
С.
Выбор той или иной формулы осуществляется в соответствии с режимными показателями и ограничениями, указанными в табл. 2.4. При движении теплоносителя в межтрубном пространстве кожухотрубчатых теплообменников с сегментными перегородками коэффициент теплоотдачи определяется [6]:
при
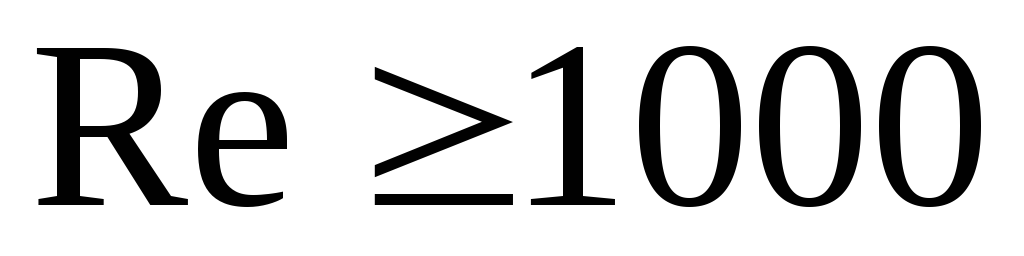
![]() ;
(2.20)
;
(2.20)
при
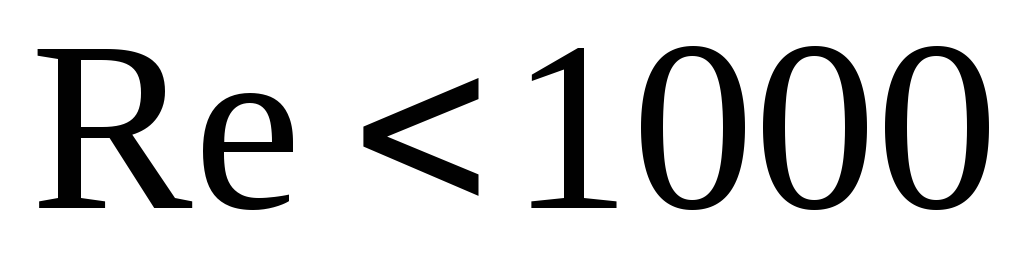
![]() .
(2.21)
.
(2.21)
В уравнениях (2.20) и (2.21) за определяющий размер принят наружный диаметр труб. Скорость теплоносителя находится для наименьшего сечения межтрубного пространства.
Таблица 2.4 Указатель формул для расчёта коэффициентов теплоотдачи
в прямых трубах и
каналах при
![]() [1]
[1]
|
№, п/п |
Значение |
Расположение поверхности теплообмена |
Пределы применения |
Номер формулы |
|
1 |
|
Горизонтальное |
|
2.15 |
|
2 |
|
Горизонтальное |
|
2.16 |
|
3 |
|
Горизонтальное |
|
2.17 |
|
4 |
|
Любое |
|
2.14 |
|
5 |
|
Вертикальное, при совпадении направлений свободной и вынужденной конвекции |
|
2.18 |
|
6 |
|
Вертикальное, при несовпадении направлений свободной и вынужденной конвекции |
EMBED Equation.3
|
2.19 |
Коэффициенты теплоотдачи в межтрубном пространстве теплообменников с оребренными трубами вычисляются по следующим зависимостям [7]
при
![]() :
:
![]() (2.22)
(2.22)
![]() (2.23)
(2.23)
при
![]() :
:
![]() (2.24)
(2.24)
![]() ,
(2.25)
,
(2.25)
где
![]() ,
,
c удельная теплоемкость теплоносителя, Дж/(кгК); D внутренний диаметр кожуха, м; B шаг перегородки, м.
Для расчета
теплоотдачи в межтрубном пространстве
гладкотрубных аппаратов без поперечных
перегородок можно использовать уравнение
[7] (2.12) - (2.19), если умножить полученное
из расчета значение
на поправочный коэффициент
![]() ,
равный
,
равный
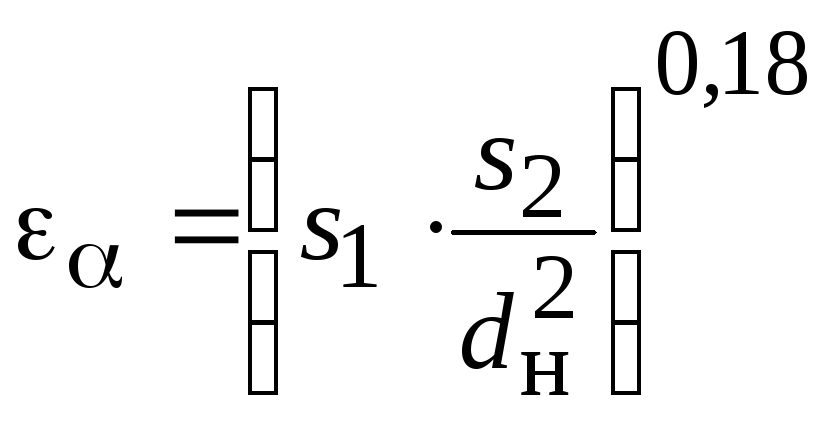 ,
(2.26)
,
(2.26)
где
![]() ,
,
![]() - продольный и поперечный шаги труб, м;
- продольный и поперечный шаги труб, м;![]()
наружный диаметр труб, м.
наружный диаметр труб, м.
В качестве геометрического размера в уравнениях (2.12) – (2.19) используется эквивалентный диаметр межтрубного пространства.
При течении среды в кольцевом канале между гладкими трубками коэффициент теплоотдачи находится по уравнению [7]
![]() ,
(2.27)
,
(2.27)
где
![]() ,
м;
,
м;
![]()
наружный диаметр внутренней трубы, м;
D
внутренний диаметр наружной трубы, м.
наружный диаметр внутренней трубы, м;
D
внутренний диаметр наружной трубы, м.
При поперечном обтекании пучка гладких труб газов находится по следующим уравнениям [1]:
для коридорных и шахматных пучков при
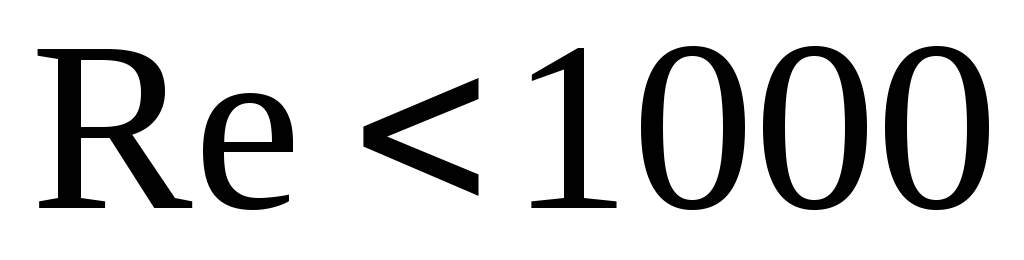
![]() ;
(2.28)
;
(2.28)
для коридорных пучков при
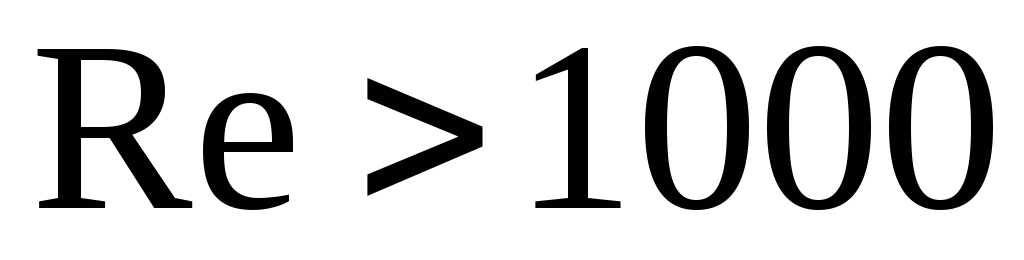
![]() (2.29)
(2.29)
для шахматных пучков при
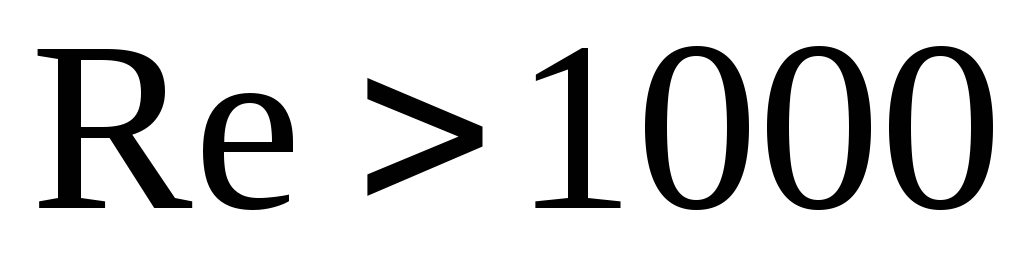
![]() ,
(2.30)
,
(2.30)
где
![]() - коэффициент, учитывающий влияние угла
атаки
(табл. 2.5).
- коэффициент, учитывающий влияние угла
атаки
(табл. 2.5).
Определяющий линейный размер в уравнениях (2.28) - (2.30) – наружный диаметр трубы.
Таблица 2.5.
Значение
коэффициентов
![]()
|
|
90 |
80 |
70 |
60 |
50 |
40 |
30 |
20 |
10 |
|
|
1 |
1 |
0,98 |
0,94 |
0,88 |
0,78 |
0,67 |
0,52 |
0,42 |
Коэффициент теплоотдачи при обтекании пучка труб с поперечными ребрами находится по уравнению [5]
![]() ;
(2.31)
;
(2.31)
где c и n коэффициенты:
для коридорных пучков
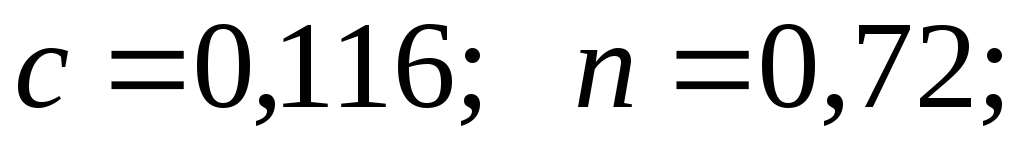
для шахматных пучков
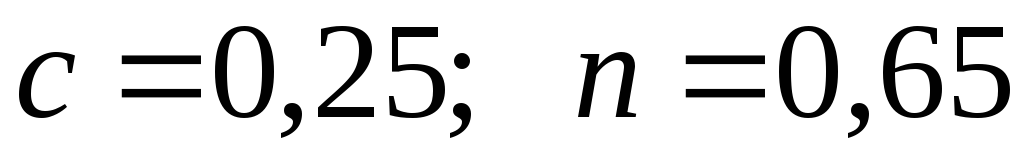 ;
;
![]() наружный диаметр
несущей трубы, м; h
высота ребра,
наружный диаметр
несущей трубы, м; h
высота ребра,
![]() ,
м;D
диаметр ребер, м; t
определяющий линейный размер: шаг между
ребрами, м.
,
м;D
диаметр ребер, м; t
определяющий линейный размер: шаг между
ребрами, м.
При течении
теплоносителя в каналах, образованных
гофрированными пластинами в пластинчатых
теплообменниках,
![]() определяют по следующим уравнениям
[6]:
определяют по следующим уравнениям
[6]:
при
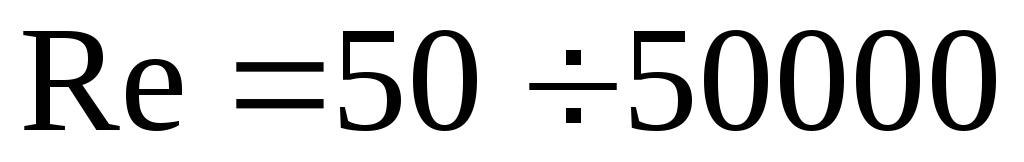 ;
;
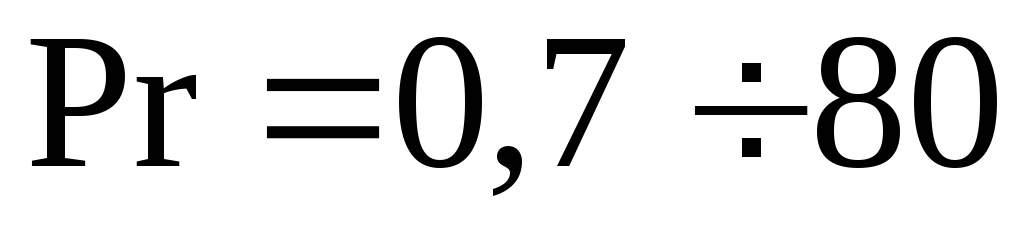
![]() ,
(2.32)
,
(2.32)
где A, b - коэффициенты, зависящие от типа пластин (табл. 2.6);
Таблица 2.6. Значение констант в уравнении (2.32) [6]
|
Тип пластины |
A |
B |
Re |
Pr |
|
0,2К |
0,086 |
0,73 |
100 30000 |
0,7 – 20 |
|
0,3 |
0,1 |
0,73 |
100 30000 |
0,7 50 |
|
0,5Е |
0,135 |
0,73 |
50 30000 |
0,7 – 80 |
|
0,5Г |
0,165 |
0,65 |
200 50000 |
0,7 50 |
для ламинарного режима
![]() ,
(2.33)
,
(2.33)
где B коэффициент, приведенный в табл. 2.7.
Таблица 2.7. Значение коэффициента В в уравнении (2.33)
-
Тип пластины
B
Re
Pr
0,2К
0,5
100
20
0,3
0,6
100
50
0,5Е
0,63
50
80
0,5Г
0,46
200
50
В вышеуказанных
уравнениях физико-химические параметры
теплоносителей определяются при
температуре
![]() .
.
