FTF 2 semestr.MARTINOV / 24

Тензорные операции

Тензоры допускают следующие алгебраические операции:

Умножение на скаляр — умножение каждого компонента тензора на скаляр. Аналогично умножению вектора или скалярной величины (и то, и другое являются частными случаями тензора);

Сложение тензоров одинаковой валентности и состава индексов (вычислять сумму можно покомпонентно, как и для векторов);

Наличие умножения на скаляр и сложения тензоров делают пространство тензоров одного и того же типа линейным пространством.

Тензорное произведение — без ограничений. Произведением тензора ранга  на тензор ранга  является тензор суммарного ранга , то есть если  и  то их произведение

Компоненты тензорного произведения суть произведения соответствующих компонент множителей, например:

Свёртка тензора — специфическая тензорная операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:

(последнее в эйнштейновских обозначениях, где суммирование по повторяющемуся верхнему и нижнему индексу подразумевается автоматически). Часто, если не как правило, свёртка (то есть результат операции свёртки) обозначается той же буквой, что и тензор, к которому свёртка применена, только, конечно, с количеством индексов, на два меньшим.

След матрицы — частный случай свёртки тензора с собой.

Свёртка двух или нескольких тензоров (в том числе тензоров и векторов), например:

 (последнее — в записи Эйнштейна).

 — операция, которую можно свести к последовательному тензорному умножению этих тензоров (см. чуть ниже) и затем свёртке получившегося тензора (возможно, несколько раз). Очевидно, эта операция линейна по всем входным каналам. Таким образом, свёртка с тензором реализует линейное или полилинейное отображение пространств тензоров на пространство тензоров (в общем случае — на другое), в частности, векторов на векторы и векторов на скаляры.

Свёртка вектора с тензором валентности два есть действие линейного оператора, определяемого этим тензором, на вектор:

 (последнее — в записи Эйнштейна).

Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:

 (последнее — в записи Эйнштейна).

Симметризация и антисимметризация — конструирование тензора того же типа с определённым видом симметрии. Для примера, симметризация тензора  — это симметричный тензор , а антисимметризация — антисимметричный тензор . В общем случае симметризация по  индексам имеет вид

а антисимметризация:

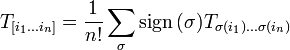
Здесь  — всевозможные перестановки индексов  а  — чётность перестановки  Разумеется, не обязательно симметризовать тензор по всем индексам, здесь это используется лишь для упрощения записи.

Если  симметричен по  то симметризация по этим индексам совпадает с  а антисимметризация даёт нулевой тензор. Аналогично в случае антисимметричности по некоторым индексам.

Если  то   Здесь  — симметричное, а  — внешнее произведение векторных пространств.