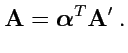FTF 2 semestr.MARTINOV / 23

Тензором ранга  называется совокупность  величин , которые при переходе из одной системы координат в другую, преобразуются по закону

Из определения тензора ранга  следует, что скаляры и векторы являются частными случаями таких величин. Действительно рассмотрим случаи с , тогдаскаляром или тензором ранга 0 называется набор из  величин , которые преобразуются по закону

вектором или тензором ранга 1 называется совокупность  величин , которые преобразуются по закону

Если компоненты вектора  расположить в виде столбца, то формулы преобразования можно записать в матричном виде

Пусть вектор  задан своими координатами а₁, а₂, a₃ системе декартовых координат с базисом ₁, ₂, ₃ ( ₁, ₂, ₃ - орты, направленные по осям координат). В другой системе прямоугольных декартовых координат с базисом e′₁, e′₂, e′₃ координаты вектора  будут

где .

Это позволяет определить вектор как совокупность трех величин а_i (i=1, 2, 3), которые определены в каждой системе декартовых координат и при переходе от одной из этих систем к другой преобразуются по указанным формулам. При таком определении вектора  назовем его тензором (аффинным ортогональным тензором) первого ранга а_i (по числу индексов в этом обозначении).

Обобщением данного определения вектора является понятие тензора второго ранга. Если в каждой системе прямоугольных декартовых координат определена совокупность величин a_ik (i, k=1, 2, 3), которые при переходе от системы координат с базисом ₁, ₂, ₃ к системе координат с базисом ₁, ₂, ₃ преобразуются по формулам

то совокупность величин a_ik называется аффинным ортогональным тензором, второго ранга (по числу входящих в это обозначение индексов).

Аналогично можно определить тензоры третьего, четвертого и т. д. рангов (и не только в трехмерном пространстве, но и в пространстве любого числа измерений).

Тензор второго ранга можно представить в форме

Тензор называется симметричным, если a_ik=a_ki, и кососимметричным, если a_ik=-a_ki.

Всякий тензор второго ранга может быть представлен в виде суммы симметричного и кососимметричного тензоров по формуле

Совокупность девяти компонентов напряжения образует симметричный тензор второго ранга - тензор напряжений