FTF 2 semestr.MAVRODI / 7

Повторный предел

Рассмотрим функцию двух переменных 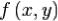, определенную в некоторой выколотой окрестности точки . Выберем и зафиксируем переменную . Получим функцию как бы одной переменной. Рассмотрим предел:

Будем считать, что существует. Теперь снимем фиксацию с переменной и рассмотрим следующий предел:

Если этот предел существует, то говорят, что есть повторный предел функции в точке .

Аналогично мы можем фиксировать сначала переменную . В этом случае мы также получим повторный предел, но, вообще говоря, другой:

Это определение можно распространить и на функции нескольких переменных .

Равенство повторных пределов

Пусть функция , определена в выколотой окрестности точки и имеет в этой точке предел (обычный). Тогда любой повторный предел в точке существует и равен обычному пределу этой функции в этой же точке.

Предел по множеству

Как и в случае одной переменной, определяется предел ФНП:

Предел по направлению:

Если множество Е – луч из А с направляющим вектором = (1 … ), то lim ( ) = – предел по направлению

→

Предел на бесконечности по Коши

Пусть числовая функция задана на множестве , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка . В этом случае число называется пределом функции на бесконечности, если для произвольного положительного

числа отыщется отвечающее ему положительное число такое, что для всех точек,

превышающих по абсолютному значению, справедливо неравенство .

Предел на бесконечности по Гейне

Пусть числовая функция задана на множестве , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка . В этом случае число называется пределом функции на бесконечности, если для всякой бесконечно большой последовательности точек соответствующая последовательность частных значений функции в этих точках сходится к числу .