FTF 2 semestr.MAVRODI / 6

Предел и непрерывность функций нескольких переменных

Пусть функция z =(х, у) определена в области D плоскости XOY, а т.лежит в области D (см. рис. 11.4). О: Число А называется пределом функции f(x, у) при стремлении т. М(х, у) к т.если для любого числа

>0 найдется такое число>0, что для всех т. М(х, у) за исключением, быть может, т.справедливо неравенство

Основные теоремы о пределах функции одной переменной (см. разд. 7.5) справедливы и для функций двух и большего числа переменных.

О: Функция z =(х, у) называется непрерывной в т. если: 1) она определена в т.и ее окрестности,

2)

О: Функция z =f(x, у) называется непрерывной на некотором множестве ЕD, если она непрерывна в каждой точке этого множества.

О: Точка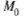называется точкой разрыва функции(М), если в ней нарушено хотя бы одно из условий 1), 2). Точки разрыва могут быть изолированными, могут образовывать линии разрыва.

Примеры: 1) Функция не определена в точках, в которых знаменатель обращается в нульу = х — линия разрыва

2)

т.— точка разрыва Для функции трех и более переменных определения предела и непрерывности аналогичны.

О: Число А называется пределом функции у =(М) при стремлении т.к т.если для любого> 0 существует такое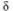> 0, что из условия

следует