FTF 1 semestr.MAVRODI / 78

Признак сравнения(для интегралов 1го рода).Пусть функции f(x) и g(x) интегрируемы по любому отрезку [a,b] и при удовлетворяют неравенствам . Тогда:

если сходится интеграл , то сходится интеграл ;

если расходится интеграл 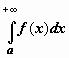, то расходится интеграл

(эти утверждения имеют простой смысл: если сходится интеграл от большей функции, то сходится интеграл от меньшей функции; если расходится интеграл от меньшей функции, то расходится интеграл от большей функции; в случаях, когда сходится интеграл от меньшей функции или расходится интеграл от большей функции, никаких выводов о сходимости второго интеграла сделать нельзя).

Док-во: если , , то функции и - монотонно возрастающие функции верхнего предела b (следствие свойств аддитивности и интегрирования неравенств). Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена

сверху. Пусть сходится. G(b) ограничена

, F(b) ограничена, т.е. сходится.

Пусть расходится F(b) неограничена G(b) неограничена, т.е. расходится.

Признак сравнения(для интегралов 2го рода). Пусть функции f(x) и g(x) интегрируемы по любому отрезку и при x > a удовлетворяют неравенствам . Тогда:

если сходится интеграл , то сходится интеграл ;

если расходится интеграл , то расходится интеграл

В качестве "стандартного" интеграла, с которым сравнивается данный, и в этом случае обычно берётся

интеграл от степенной функции типа . Этот интеграл сходится, если p < 1, и расходится,

если :