ЛР-7 / Тема 4

Тема 4. Элементы теории массового обслуживания

Исторически эта теория берет начало от работ, в которых рассматривалась проблема перегрузки телефонных линий, весьма обострившаяся в начале столетия. С этого времени интерес к проблемам массового обслуживания быстро растет, так как стало ясно, что задачи, рассматриваемые в теории массового обслуживания, выходят за рамки сферы обслуживания и имеют более широкую область применения.

Процесс работы системы массового обслуживания представляет собой случайный процесс. Теорией случайных процессов называется математическая наука, изучающая закономерности случайных явлений в динамике их развития.

Теория случайных процессов представляет собой раздел теории вероятностей особенно бурно развивающийся в последние десятилетия в связи со все расширяющимся кругом его практических приложений.

При изучении явлений окружающего мира часто приходится сталкиваться с процессами, течение которых заранее предсказать в точности невозможно. Эта неопределенность (непредсказуемость) вызвана влиянием случайных факторов, воздействующих на ход процесса. Например, население города (или области) меняется с течением времени случайным (непредсказуемым) образом под влиянием таких факторов, как рождаемость, смертность, миграция и т. д.

Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.

Процесс называется процессом с дискретными состояниями, если его возможные состояния можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны.

Процесс работы системы массового обслуживания представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние системы массового обслуживания меняется скачком в случайные моменты появления каких-то событий.

Математический анализ работы системы массового обслуживания существенно упрощается, если процесс этой работы — марковский. Марковские процессы нашли применение и в исторических исследованиях, например при анализе динамики социальных процессов, так как они являются наиболее простыми среди моделей, учитывающих взаимосвязи различных социальных групп.

4.1 Понятие марковского случайного процесса

Случайный процесс называется марковским или случайным процессом без последствия, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние.

Случайные процессы с дискретными состояниями анализируют, используя схему называемую графом состояний. Граф состояний это схема, на которой условно изображают возможные состояния системы и показывают возможные переходы между состояниями. Обычно состояния системы изображаются кружками (прямоугольниками), а возможные переходы из состояния в состояние - стрелками (ориентированными дугами), соединяющими состояния.

Пример 1

Построить граф состояний следующего случайного процесса: Система состоит из двух частей, каждая из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ее восстановление, продолжающееся заранее неизвестное случайное время.

Решение. Возможные состояния системы: S₀ - обе части нормально функционируют; S₁- первая часть восстанавливается, вторая нормально функционирует; S₂ - вторая часть восстанавливается, первая нормально функционирует; S₃ - обе части восстанавливается. Граф системы приведен на р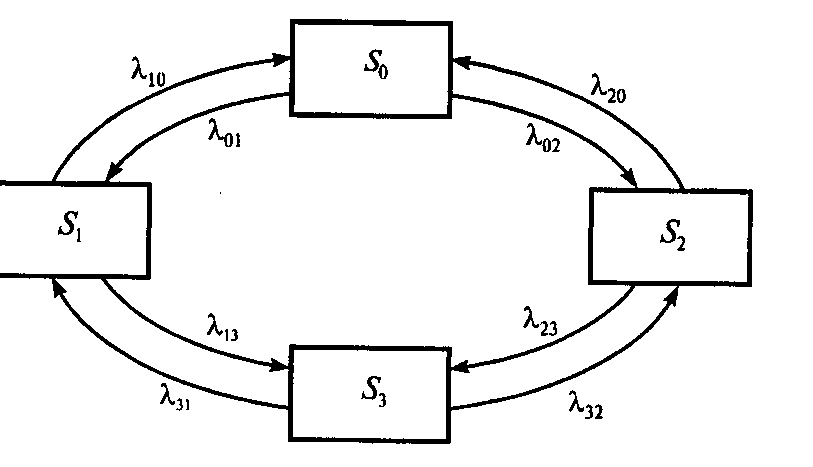ис.1.

Рис.1

Стрелка, направленная, например, из S₀ в S₁, означает переход системы в момент отказа первой части от нормального функционирования, из S₁ в S₀ — переход в момент окончания восстановления этой части.

На графе отсутствуют стрелки из S₀ в S₃ и из S₃ в S₀. Это объясняется тем, что отказы частей системы от нормального функционирования предполагаются независимыми друг от друга и, например, вероятностью одновременного отказа частей системы от нормального функционирования (переход из S₀ в S₃) или одновременного восстановления функций частей системы (переход из S₃ в S₀₎ можно пренебречь.

Для математического описания марковского случайного процесса с дискретными состояниями и непрерывным временем, протекающего в системах массового обслуживания, познакомимся с понятием потока событий.

Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

Поток характеризуется интенсивностью — частотой появления событий или средним числом событий, поступающих в системы массового обслуживания в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.

Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока есть величина постоянная: (t)= .

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени ₁ и ₂ - число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.).

Поток событий называется ординарным, если вероятность попадания на малый '(элементарный) участок времени t двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами.

Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. Название "простейший" объясняется тем, что системы массового обслуживания с простейшими потоками имеет наиболее простое математическое описание. Заметим, что регулярный поток не является "простейшим", так как он обладает последействием: моменты появления событий в таком потоке жестко зафиксированы.

Простейший поток в качестве предельного возникает в теории случайных процессов для суммы случайных величин: при наложении (суперпозиции) достаточно большого числа n независимых, стационарных и ординарных потоков, сравнимых между собой по интенсивностям _i (i=1,2, ..., n). Получается поток, близкий к простейшему с интенсивностью равной сумме интенсивностей входящих потоков, т.е.

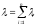
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния S_i в S_j происходят под воздействием простейших потоков событий с интенсивностями _ij (i,j,=0, 1, 2, 3); так, переход системы из состояния S₀ в S₁ будет происходить под воздействием потока отказов первого части, а обратный переход из состояния S₁ в S₀ - под воздействием потока восстановления нормального функционирования первой части и т. д. Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система S имеет четыре возможных состояния: S₀, S₁, S₂, S₃

Вероятностью i-го состояния называется вероятность р_i(t) того,что в момент t система будет находиться в состоянии S_i. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице:

Составим систему дифференциальных уравнений Колмогорова для вероятностей состояний изучаемой системы, граф состояний которой изображен на рис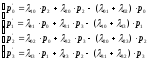.1:

(1)

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности 1-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (1-го состояния).

В полученной системе независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение

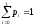. (2)

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент t= 0. Так, например, систему уравнений (1) естественно решать при условии, что в начальный момент об части функционируют нормально система находится в состоянии S₀, т.е. при начальных условиях: p₀(0) =1, p₁(0) = p₂(0) = p₃(0) = 0.

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы p_i(t) в предельном стационарном режиме, т.е. при t, которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния S_i имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния S₀,т.е p₀ =0,5 то это означает, что в среднем половину времени система находится в состоянии S₀.

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим.

Для системы S с графом состояний, изображенном на рис. 1, такая система уравнений имеет вид:

(3)

Систему (3) составляют непосредственно по графу состояний, используя правило: справа в уравнениях записывают предельную вероятность данного состояния р_i умноженную на суммарную интенсивность всех потоков, ведущих из данного состояния, а слева - сумму произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2

Найти предельные вероятности для системы, граф состояний которой изображен на рис.1, при ₀₁=1, ₀₂=2, ₀₁=1, ₁₀=2, ₁₃=2, ₂₀=3, ₂₃=1, ₃₁=3, ₃₂=2

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (3) или с учетом условия задачи:

(4)

(Здесь мы вместо последнего уравнения системы (3) записали нормировочное условие (2)).

Решив систему (4), получим p₀(0) =0,4, p₁(0) =0,2, p₂(0) = 0,27, p₃(0) =0,13, т.е. в предельном, стационарном режиме система в среднем: 40% времени будет находиться в состоянии S₀ (обе части функционируют нормально); 20% — в состоянии S₁ (первая часть восстанавливается, вторая функционирует нормально); 27% — в состоянии S₂ (вторая часть восстанавливается, первая функционирует нормально) и 13% времени -- в состоянии S₃ (обе части системы восстанавливаются).