
- •Лабораторный практикум по физике
- •“Электричество и магнетизм”
- •Описание экспериментальной установки
- •Описание экспериментальной установки
- •Оценить мостовой метод измерения сопротивлений.
- •Описание экспериментальной установки и порядок выполнения работы
- •Описание экспериментальной установки и порядок выполнения работы
- •1. Движение частицы в электрическом поле
- •Описание экспериментальной установки
- •Описание экспериментальной установки и порядок выполнения работы
- •Контрольные вопросы
- •Описание экспериментальной установки
- •Оглавление
И.М. Хабибулин, В.Ю. Звеков,
В.В. ВОЙТЮК, С.А. ШЕЛОМЕНЦЕВ
Лабораторный практикум по физике
“Электричество и магнетизм”
Методическое пособие составлено для лабораторных работ по разделу “Электричество и магнетизм” курса общей физики. В нем изложены некоторые теоретические вопросы по этому разделу, порядок выполнения лабораторных работ.
Методическое пособие может быть использовано для самостоятельной работы над разделом “Электричество и магнетизм” и как руководство при выполнении лабораторных работ.
Составители: И.М.Хабибулин
В.Ю.Звеков
В.В.Войтюк
С.А.Шеломенцев
Рецензент В.Я.Мартенс
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 3.1
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: Построение силовых линий и эквипотенциальных поверхностей электрического поля созданного электродами различной формы.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: электролитическая ванна, электроды различной формы, блок питания, цифровой вольтметр.
Электрические заряды взаимодействуют между собой посредством электрического поля, которое представляет собой особую форму материи. В случае неподвижных зарядов поле называют электростатическим.
Электрическое
поле характеризуется в каждой своей
точке двумя характеристиками: силовой
-
вектором электрической напряженности
![]() и энергетической (скалярной) -
потенциалом .
и энергетической (скалярной) -
потенциалом .
Напряженностью
![]() электрического поля в данной точке
называется векторная величина, числено
равная и совпадающая по направлению с
силой
электрического поля в данной точке
называется векторная величина, числено
равная и совпадающая по направлению с
силой
![]() ,
действующей со стороны поля на единичный
положительный заряд q0
,
помещенный в рассматриваемую точку
поля:
,
действующей со стороны поля на единичный
положительный заряд q0
,
помещенный в рассматриваемую точку
поля:
![]() .
.
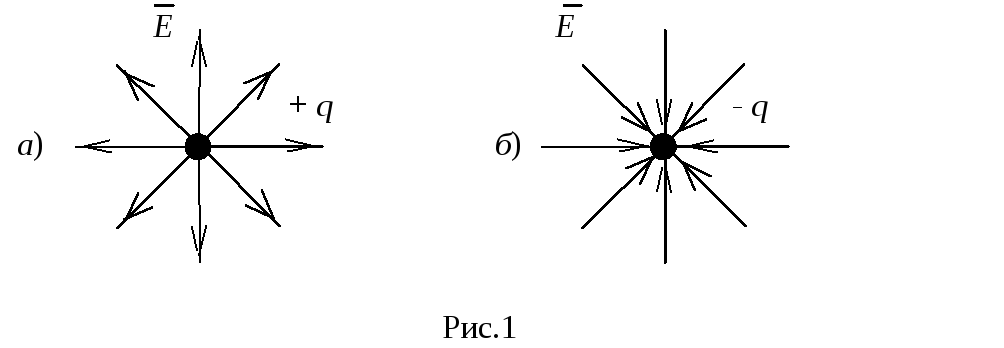
Принято считать, что вектор напряженности направлен от положительного заряда (рис.1-а) и к отрицательному заряду (рис.1-б).
Если
электрическое поле создано системой
зарядов, т.е. существует несколько полей,
то вектор напряженности
![]() результирующего
поля равен геометрической сумме
напряженностей полей, созданных в данной
точке каждым из зарядов в отдельности:
результирующего
поля равен геометрической сумме
напряженностей полей, созданных в данной
точке каждым из зарядов в отдельности:
![]() =
=
![]() 1
+
1
+
![]() 2
+
2
+
![]() 3
+ ... +
3
+ ... +
![]() n
n
Это соотношение носит название принципа суперпозиции электрических полей. С его помощью можно в общем виде рассчитать электрические поля сколь угодно сложных систем электрических зарядов.
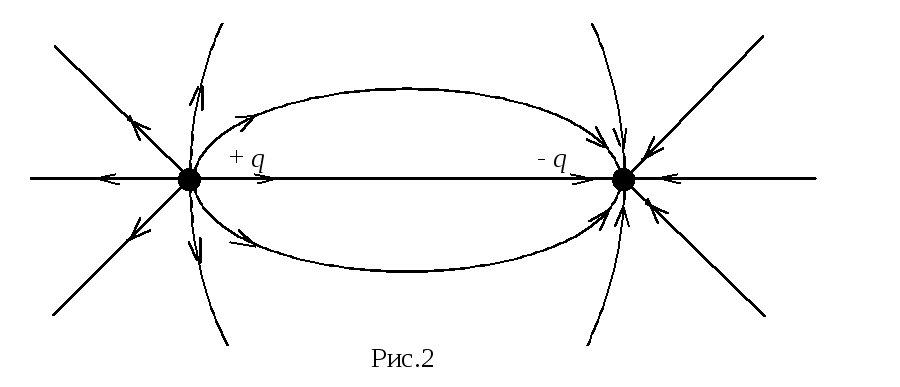
Таким образом, для описания электрического поля нужно задать вектор напряженности в каждой точке поля. Сделать это можно аналитически или графически, используя силовые линии. Силовой линией, или линией вектора напряженности электрического поля, называют линию, для которой направление касательной в любой точке совпадает с направлением вектора напряженности поля (рис.2).
Густота силовых линий, проходящих через единицу поверхности перпендикулярной к силовым линиям, пропорциональна величине напряженности поля в данном месте. Изображения силовых линий поля (карта поля), наглядно показывают, чему равна напряженность в разных частях поля и как она изменяется в пространстве. Вследствие наглядности этот способ представления полей широко применяется в электротехнике.
Потенциалом электростатического поля в данной точке называется скалярная величина, числено равная отношению потенциальной энергии W положительного заряда к величине заряда q0 , помещенного в данную точку поля:
![]() ,
,
т.е. потенциал не зависит от величины пробного заряда q0 и характеризует свойства поля в данной его точке.
Связь между напряженностью поля и потенциалом выражается как:
![]() ,
,
т.е. напряженность поля это быстрота изменения потенциала по координате dr или в общем виде:
![]() =
-
grad ,
=
-
grad ,
знак
”минус” означает, что вектор напряженности
![]() электрического поля направлен в сторону
убывания потенциала .
электрического поля направлен в сторону
убывания потенциала .
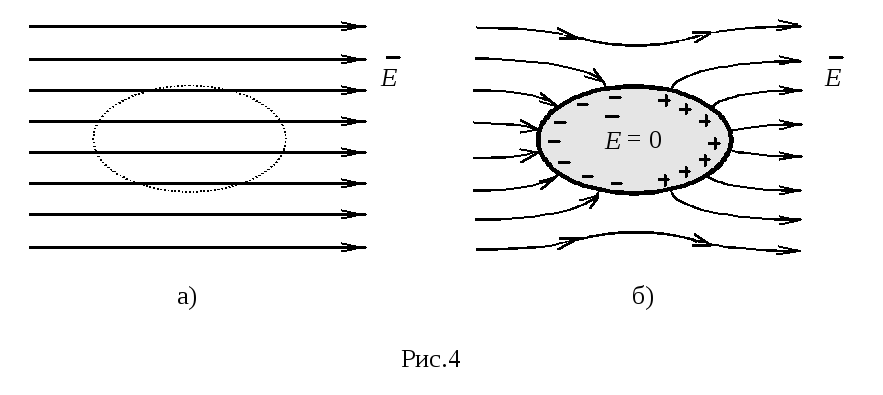
Если
внести в электростатическое поле
(рис.4-а)
проводник, то в нем произойдет разделение
положительных и отрицательных зарядов.
Появившиеся в результате разделения
заряды называют индуцированными
зарядами. Разделение зарядов происходит
до тех пор, пока их электрические поля
не скомпенсируют внешнее поле. В
установившемся состоянии результирующее
поле внутри проводника равно нулю (![]() =
0) и заряды находятся в равновесии.
=
0) и заряды находятся в равновесии.
![]() ,
сквозь замкнутую поверхность равен
алгебраической сумме зарядов внутри
этой поверхности, делённой на 0
:
,
сквозь замкнутую поверхность равен
алгебраической сумме зарядов внутри
этой поверхности, делённой на 0
:
![]() =
=
![]() .
.
А
так как в проводнике всюду
![]() =
0, то поток вектора
=
0, то поток вектора
![]() через любую замкнутую поверхность в
проводнике, также равен нулю, т.е. согласно
(7) внутри проводника избыточных зарядов
нет. Избыточные заряды появляются лишь
на поверхности проводника.
через любую замкнутую поверхность в
проводнике, также равен нулю, т.е. согласно
(7) внутри проводника избыточных зарядов
нет. Избыточные заряды появляются лишь
на поверхности проводника.
Отсутствие
поля внутри проводника означает, что
потенциал
в проводнике одинаков во всех его точках,
т.е. любой проводник в электростатическом
поле представляет собой эквипотенциальную
область и его поверхность является
эквипотенциальной. Из этого факта
следует, что непосредственно у этой
поверхности линии напряженности
![]() перпендикулярны этой поверхности
(рис.4-б).
перпендикулярны этой поверхности
(рис.4-б).
При внесении в электрическое поле диэлектрика (рис 5-а), в нем появятся поверхностные связанные заряды, объёмные же избыточные заряды во всех точках такого диэлектрика будут равны нулю.
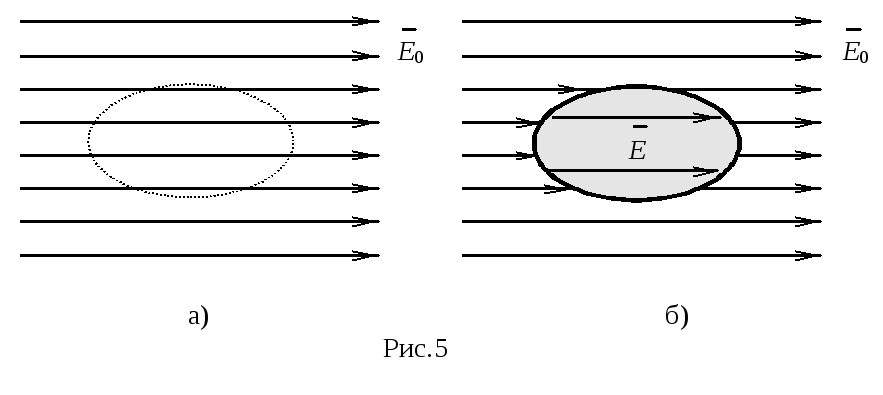
![]() ,
,
где - диэлектрическая проницаемость вещества.
Потенциал в среде:
![]() ,
,
где 0 - потенциал электрического поля при отсутствии диэлектрика.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Метод исследования электростатического поля с помощью силовых линий и эквипотенциальных поверхностей полезен при изучении сложных электростатических полей, точный расчет которых затруднителен из-за сложности граничных условий (многоэлектродные радиолампы, электростатические линзы, фотоэлектронные умножители). При этом принципиальное значение имеет правило подобия потенциальных полей, позволяющее в большом масштабе воспроизводить подлежащие изучению поля. Правило подобия утверждает, что если размеры электродов, создающих поле, и все расстояния между электродами изменены в одной пропорции, то структура поля остаётся прежней.

Проверив исправность соединения электродов 1 и 2 с блоком питания 4 и исправность соединения электрода 1 и подвижного электрода (зонда) 3 с клеммами 9 вольтметра, включить установку тумблером 8. Блок питания 4 системы электродов, находящихся в электролитической ванне 5, создаёт электрическое поле между электродами. Подвижный электрод 3, соединенный с цифровым вольтметром 6, служит для нахождения точек одинакового потенциала в электростатическом поле создаваемом электродами 1 и 2.
Перемещая зонд, необходимо зафиксировать и нанести на свою масштабную сетку 8-10 точек для каждого из требуемых потенциалов, исходя из положения зонда на масштабной сетке в электролитической ванне, выбирая 5-7 значений потенциала таким образом, чтобы эквипотенциальные поверхности охватывали всю площадь ванны.
На своей масштабной сетке, соединив точки с равными потенциалами, провести эквипотенциальные линии и силовые линии электрического поля.
Для изучения электрического поля в присутствии проводящих и непроводящих поверхностей, поместить кольцо 7 (металлическое или из диэлектрика) и провести определение положения эквипотенциальных поверхностей.
В выводах сравнить абсолютные значения диэлектрической проницаемости диэлектриков и характер их зависимости от напряженности электрического поля.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Какие поля называются электростатическими?
Сформулируйте и докажите теорему Остроградского-Гаусса.
Каковы основные характеристики электростатического поля?
Каково условие потенциальности силового поля? Докажите, что электростатическое поле является потенциальным.
Какова связь между потенциалом и напряженностью электростатического поля? Как направлены линии напряженности к поверхности электродов и металлического кольца? Как влияет материал кольца на карту поля?
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 3.2
ИЗУЧЕНИЕ ДИЭЛЕКТРИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ
Цель работы: Снять зависимость диэлектрической проницаемости от напряженности электрического поля различных диэлектриков.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: плоские конденсаторы, заполненные титанатом бария и слюдой, блок питания, вольтметр, миллиамперметр
Диэлектриками (или изоляторами) называют вещества. практически не проводящее электрического тока. Объясняется это наличием в диэлектриках только связанных зарядов, не способных перемещаться, создавая ток.
Сами диэлектрики можно подразделить на полярные и неполярные. Полярными называют диэлектрики, которые состоят из полярных молекул, т.е. обладающих собственным дипольным моментом. Неполярные диэлектрики состоят из молекул, центры тяжести положительных и отрицательных зарядов у которых совпадают, и, следовательно, не имеют собственного дипольного момента. Но неполярные диэлектрики под действием внешнего электрического поля поляризуются вследствие смещения центров тяжести отрицательных и положительных зарядов.
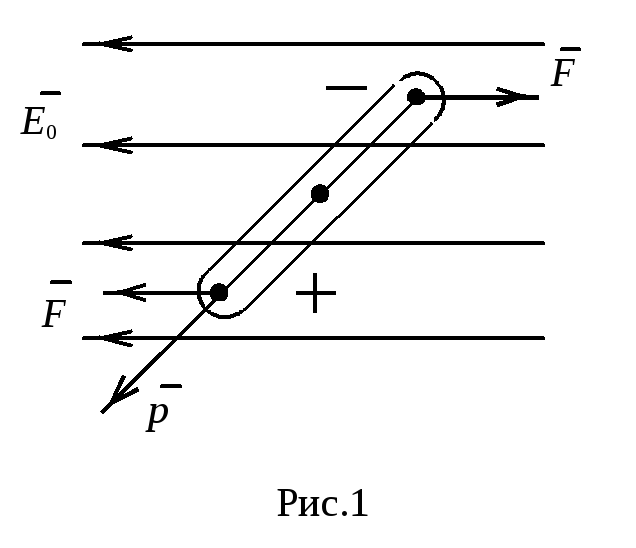
Молекулы диэлектрика во внешнем электрическом поле подобны диполям. Электрическим диполем называют систему двух равных по величине и противоположных по знаку точечных электрических зарядов +q и -q находящихся на расстоянии l друг от друга. Диполь характеризуется моментом диполя
![]() =
q
=
q
![]() ,
,
где
![]() -
плечо диполя -
вектор направленный по оси диполя от
отрицательного заряда к положительному
и численно равный расстоянию между
ними.
-
плечо диполя -
вектор направленный по оси диполя от
отрицательного заряда к положительному
и численно равный расстоянию между
ними.
При внесении диэлектрика во внешнее электрическое поле происходит поляризация - смещение зарядов - положительных по полю, отрицательных против поля, т.е. дипольные моменты молекул будут стремиться ориентироваться вдоль силовых линий внешнего электрического поля (рис.1) или появятся дипольные моменты в неполярных диэлектриках. В результате поляризации электрический момент единицы объема диэлектрика становится отличным от нуля:
![]() =
=
![]()
где
![]() -
вектор поляризации,
-
вектор поляризации,
![]() -
дипольный момент
i-ой
молекулы.
-
дипольный момент
i-ой
молекулы.
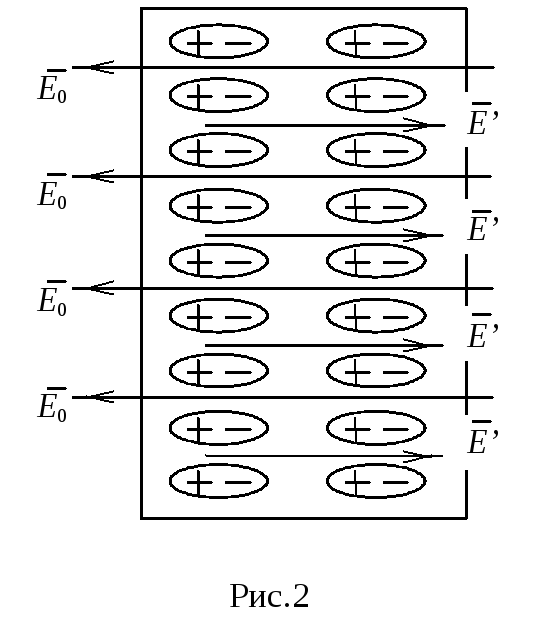
![]() 0
возникают нескомпенсированные связанные
заряды. Появление этих зарядов приводит
к появлению внутреннего электрического
поля
0
возникают нескомпенсированные связанные
заряды. Появление этих зарядов приводит
к появлению внутреннего электрического
поля
![]() ’
связанных зарядов, направленного
противоположно внешнему полю
’
связанных зарядов, направленного
противоположно внешнему полю
![]() 0
(рис.2).
В результате на заряды внутри диэлектрика
будет действовать результирующее поле
0
(рис.2).
В результате на заряды внутри диэлектрика
будет действовать результирующее поле
![]() :
:
![]() =
=
![]() 0
+
0
+
![]() ’.
’.
Для
большого класса диэлектриков поляризация
![]() пропорциональна напряженности
пропорциональна напряженности
![]() поля
в диэлектрике:
поля
в диэлектрике:
![]() =
0
=
0![]()
где - безразмерная величина, называемая диэлектрической восприимчивостью вещества, характеризующая свойства диэлектрика ( > 0), 0 - электрическая постоянная.
Кроме
диэлектрической восприимчивости
для
характеристики диэлектрика используется
диэлектрическая проницаемость
,
которая определяется как отношение
внешнего электрического поля
![]() 0
в
вакууме к результирующему полю
0
в
вакууме к результирующему полю
![]() в
диэлектрике:
в
диэлектрике:
=
![]() .
.
Диэлектрическая проницаемость связана с восприимчивостью соотношением:
= 1 + .
Существует
класс диэлектриков для которых связь
между поляризацией
![]() и напряженностью
и напряженностью
![]() не является линейной. К группе таких
материалов относятся: сегнетова соль,
титанат бария и др.
не является линейной. К группе таких
материалов относятся: сегнетова соль,
титанат бария и др.
Отличие сегнетоэлектриков от остальных диэлектриков следующее:
- сегнетоэлектрики характеризуются очень большой величиной диэлектрической проницаемости (до сотен тысяч);
-
диэлектрическая проницаемость
и
восприимчивость
зависят
от напряженности
![]() 0
внешнего
электрического поля;
0
внешнего
электрического поля;
-
поляризация
![]() сегнетоэлектрика зависит от предыстории
диэлектрика, т.е. от предшествующих
значений
сегнетоэлектрика зависит от предыстории
диэлектрика, т.е. от предшествующих
значений
![]() (это явление называют гистерезисом).
(это явление называют гистерезисом).
Необычные свойства сегнетоэлектриков объясняются тем, что они состоят из макроскопических областей спонтанной поляризации - “доменов”. При внесении сегнетоэлектрика во внешнее электрическое поле, ориентируются сразу целые поляризованные области (“домены”). Поэтому даже в слабых электрических полях сегнетоэлектрики обладают высокой диэлектрической проницаемостью.
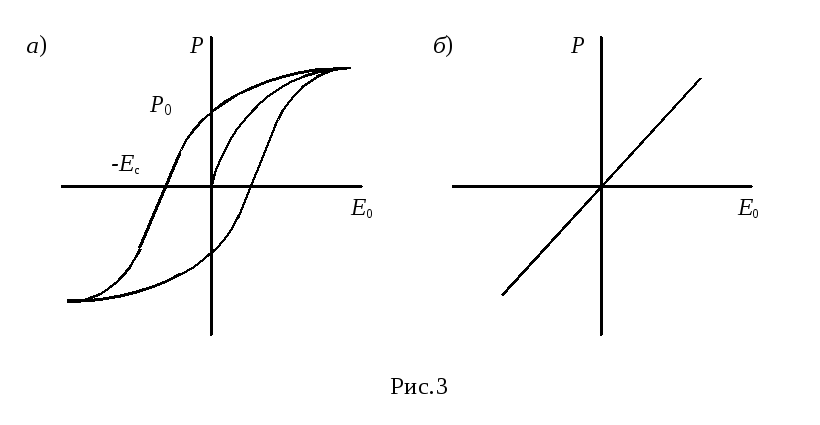
На рис.3-а показана кривая зависимости поляризации P от напряженности Е0 внешнего электрического поля - петля гистерезиса, где P0 - остаточная поляризация, Eс - напряженность электрического поля обратного направления, при которой исчезает поляризация сегнетоэлектрика (коэрцитивная сила). На рис.3-б показана аналогичная зависимость для обычного диэлектрика.
Для определения зависимости диэлектрической проницаемости среды от напряженности Е0 электрического поля диэлектрик можно поместить между пластин плоского конденсатора, подключенного к источнику переменного тока.
Емкость такого конденсатора
С
=![]() ,
(1)
,
(1)
где S - площадь пластины конденсатора, d - расстояние между пластинами.
Емкостное сопротивление конденсатора
RC
=
![]() =
=
![]() ,
(2)
,
(2)
где - циклическая частота переменного тока, - частота переменного тока.
Согласно закону Ома для участка цепи
I
=
![]() .
(3)
.
(3)
где U - напряжение на конденсаторе, I - ток через конденсатор.
Решая совместно уравнения (1), (2), (3), получим
=
![]() =
=
![]() =
=
![]() =
=
![]() .
(4)
.
(4)
Напряженность Е0 электрического поля связана с напряжением на пластинах конденсатора соотношением
Е0
=
![]() .
(5)
.
(5)
Таким образом, зная геометрические размеры (S и d) конденсатора, частоту переменного тока, падение напряжения U и ток I через конденсатор, можно определить значение диэлектрической проницаемости диэлектрика при различных значениях напряженности Е0 электрического поля.
