Типы чисел с плавающей запятой
Стандарт IEEE 754-1985 определяет
Представление нормализованных положительные и отрицательные числа с плавающей точкой.
Представление нормализованных положительные и отрицательные числа с плавающей точкой.
Представлениенулевыхчисел,
Представление специальной величины - бесконечность (Infiniti),
Представление специальной величины "Не число" (NaN – No a Number),
IEEE 753-1985 определяет 4 формата представления чисел с плавающей запятой:
с одинарной точностью (single-precision) 32 бита,
с двойной точностью (double-precision) 64 бита,
с одинарной расширенной точностью (single-extended precision) >=43 бит (редко используемый),
с двойной расширенной точностью (double-extended precision) >= 79 бит (обычно используют 80 бит).
Основное применение в технике и программирование получили форматы 32 и 64 бита. Например, в С# используют типы данных single и double.
Основные понятия в представлении чисел с плавающей точкой.
Возьмем, к примеру, десятичное число 155.625. Представим это число в нормализованном экспоненциальном виде: 1.55625*102=1.55625e+2.
Число 1.55625e+2 состоит из двух частей: мантиссы M=1.55625 и экспоненты e =+2.
Нормализованные числа Если мантисса находится в диапазоне 1<=M<2 то число считается нормализованным.
Денормализованные числа. Это числа, мантиссы которых лежат в диапазоне 0.1 <= M <1 Денормализованные числа находятся ближе к нулю, чем нормализованные. Денормализованные числа как бы разбивают минимальный разряд нормализованного числа на некоторое подмножество. Сделано так потому, что в технической практике чаще встречаются величины близкие к нулю.
Экспонента представлена основанием системы исчисления (в данном случае 10) и порядком (в данном случае +2). Порядок экспоненты может иметь отрицательное значение, например число 0,0155625=1,55625e-2.
Формальное представление нормализованных чисел в формате IEEE 754.
S - бит знака числа (0 - положительное число; 1 - отрицательное число).
E - смещенная экспонента (смещение для устранения знака порядка). Порядок = E - 2(b-1) + 1 , где E- экспонента двоичного нормализованного числа с плавающей точкой, 2(b-1)-1 - смещение экспоненты.
M - остаток мантиссы двоичного нормализованного числа с плавающей точкой (Первый бит мантиссы всегда 1, поэтому он скрывается).
Формула вычисления десятичных чисел с плавающей точкой из чисел, представленных в стандарте IEEE754:
Формула расчета нормализованных чисел:
Формула расчета денормализованных чисел:
Формат числа одинарной точности (single-precision) 32 бита
Формат числа двойной точности (double-precision) 64 бита
Исключения чисел формата IEEE754. Если применить формулу нормализованных чисел для вычисления минимального и максимального числа в формате single, представленного в IEEE754, то получим следующие результаты:
00 00 00 00 hex= 5,87747175411144e-39 (минимальное положительное).
80 00 00 00 hex=-5,87747175411144e-39 (минимальное отрицательное).
7f ff ff ff hex= 6,80564693277058e+38 (максимальное положительное).
ff ff ff ff hex=-6,80564693277058e+38 (максимальное отрицательное).
Отсюда видно, что невозможнопредставить число нуль в заданном формате.
Поэтому из стандарта сделаны исключения, и формула не применяется в следующих случаях:
Число IEEE754=00 00 00 00hex считается числом +0.
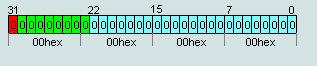
Число IEEE754=80 00 00 00hex считается числом -0.
Числа, которые выходят за границы диапазона представления чисел считаются бесконечными. Число IEEE754=7F 80 00 00hex считается числом +∞.
Число
IEEE754=FF 80 00
00hex считается числом -∞.
NAN (No a Number) – не число.Числа IEEE754=FF (1xxx)X XX XXhex не считается числами, кроме +∞. Числа IEEE754=7F (1xxx)X XX XXhex не считается числами, кроме -∞. Числа, представленные в битах с 0...22, могут быть любыми кроме 0.
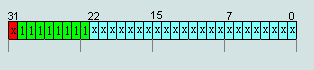
Числа IEEE754=(x000) (0000) (0xxx)X XX XXhex считаются денормализованными числами, за исключением чисел -0 и +0
Полный диапазон чисел в формате 32 бит по стандарту IEEE754:
В таблице представлены приблизительные диапазоны типов с плавающей запятой.
|
Тип |
Диапазон |
Точность |
|
float |
±1,5e−45 … ±3,4e38 |
7 знаков |
|
double |
±5,0e−324 … ±1,7e308 |
15 -16 знаков |