5.12. Сравнение методов повышения верности в системах пдс

Необходимость сравнения различных методов повышения верности возникает при проектировании систем ПДС. В этом случае разработчик должен выбрать такой метод повышения верности доставки сообщения при требуемой скорости передачи и, как правило, ограничениях на стоимость аппаратуры.

Решение данной задачи в общем случае для произвольной статистики ошибок в канале связи, различных алгоритмах работы систем, а также экономических ограничениях представляется чрезвычайно громоздкими , и во многих случаях не разрешимой задачей. На практике пользуются приближенными оценками параметров различных систем ПДС.

На первом этапе задаются моделью возникновения ошибок в дискретном канале связи. В качестве моделей, как правило, используют либо модель биномиального канала (независимые ошибки), либо модель с группированием ошибок (чаще всего модель Пуртова Л.П.)

Далее выбирают систему ПДС по заданной верности передачи. Скорость передачи считают постоянной. Однако пользоваться для этой цели вероятностью необнаруживаемой ошибки неудобно. Действительно, пусть имеется сообщение длиной 400 единичных элементов и надо сравнить две системы без обратной связи с кодами исправления ошибки.

1 система передает сообщения блоками длиной 5е.э. (код МТК-2) и обеспечивает Р_пр(к) = 0,999 на каждый блок.

2 система передает сообщения блоками длиной 200 е.э. и обеспечивает Р_пр(к) = 0,99 на каждый блок.

На первый взгляд 1 система обеспечивает большую верность передачи. Однако, определим какова вероятность правильного приема всего сообщения, состоящего из 400 е.э. при независимых ошибках в канале.

Для 1 системы

Р_пр^сообщ = [Р_пр(к)]^Nбл

Все сообщение можно передать N_бл = 400/5=80бл

Тогда Р_пр^сообщ = 0,999⁸⁰= 0,923

Для 2 системы

Все сообщение передается N_бл = 400/200=2бл

Тогда Р_пр^сообщ =0,99² =0,98

Т.о., 2 система обеспечивает лучшую верность доставки, хотя имеет худшую вероятность правильного приема по блокам.

Для объективного сравнения систем по верности доставки сообщения при различной длине кода Л.М.Финком был предложен простой критерий – эквивалентная вероятность ошибки ρ_э – это вероятность ошибки в расчете на один информационный сегмент сообщения после принятия мер повышения верности.

ρ_э= 1-[Р_пр(к)]^1/к (5.19)

Р_пр(к) – вероятность выдачи получателю блока длиной k е.э. без ошибки

Р_пр(к)= 1- Р_н.о.(к), (5.20)

где Р_н.о.(к) – вероятность необнаружения ошибки в блоке длиной k, выдаваемом получателю.

Подставляя (5.20) в (5.19), получим

ρ_э=1-[1- Р_н.о.(к)]^1/к ≈ 1-1/k Р_н.о.(к)

Используя бином Ньютона,с учетом Р_н.о.(к)<<1, получаем

ρ_э= Р_н.о.(к) / k (5.22)

Из формулы (5.22) следует физический смысл эквивалентной вероятности ошибки: эквивалентная вероятность ошибки определяет вероятность ошибки единичного элемента в дискретном симметричном канале без памяти, в котором система с примитивным кодированием эквивалентна заданной системе с повышением верности.

Определим для приведенного примера ρ_э

1 система – к = 5 , Р_пр(к)=0,999, тогда Р_н.о.(к)=0,001

ρ_э¹ = Р_н.о.(к) / к = 0,001/5 =2 * 10^-4

2 система – к = 200, Р_пр(к)=0,99, тогда Р_н.о.(к)=0,01

ρ_э² = Р_н.о.(к) / к = 0,01 / 200 =5 *10^-5

Таким образом, ρ_э² < ρ_э¹ , и можно сделать вывод, что вторая система обеспечивает лучшее повышение верности.

Эквивалентная вероятность ошибки является удобной мерой для сравнения между собой не только различных кодов, но и различных систем связи, в которых могут использоваться различные каналы, различные методы модуляции и различные методы повышения верности.

При сравнении и выборе систем ПДС по средней относительной скорости необходимо фиксировать вероятность ошибки, т.е. сравнивают скорости доставки сообщений при обеспечении заданной верности доставки. Обычно в качестве критерия используют среднюю относительную скорость доставки, т.е. “R”

В качестве примера сравним систему с избыточным кодированием и исправления ошибок (т.е. систему без ОС) и систему РОС-ПП (т.е. систему с ОС).

Для системы с кодом, исправляющим ошибки

R₁ = k₁ / n₁

Пусть индекс 1 – относится к системе без ОС, а индекс 2 – к системе с ОС

Для системы РОС-ПП имеем:

R₂ = k₂ [1- P_ст( n₂ )] / n₂ [1+(h-1) P_ст( n₂ )]

Определим, при каких условиях РОС-ПП эффективнее системы с исправляющим кодом. Для этого

R₂ > R₁ , т.е.

k₂ [1- P_ст( n₂ )] > k₁

n₂ [1+(h-1) P_ст( n₂ )] n₁

Естественно, что сравнивать необходимо при одинаковых k, поэтому k₁ = k₂ и тогда :

n₁ > n₂ [1+(h-1) P_ст( n₂ )] / [1- P_ст( n₂ )]

Учитывая, что P_ст( n₂ ) ≈ n₂ р_о ( р_о – вероятность ошибки в канале), имеем:

n₁ > n₂ [1+(h-1) n₂ р_о] / [1 - n₂ р_о]

Для этого примера строим график. Например, в результате сравнения системы РОС – ПП и системы с кодом, исправляющим ошибки можно получить следующий график

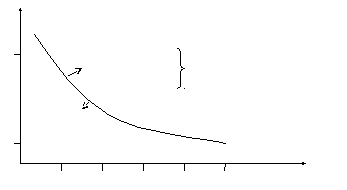Р₀

10^–2

Эффективны

системы с кодом без ОС.

исправляющим ошибки

Эффективны

системы с ОС

10^–3

n₂

10 20 30 40 50

Р₀ – вероятность ошибки в канале на один е.э.

n₂ – длина блока в системе РОС – ПП

Рис. 5.12. Сравнение систем с ОС и без ОС

До сих пор при сравнении систем ПДС мы не рассматривали экономические соображения, т.е. возможную сложность технической реализации. При учете этих факторов задача выбора системы ПДС значительно усложняется.

Подводя итог, отметим некоторые общие закономерности при выборе систем повышения верности:

1. Системы без ОС экономически выгодно применять в следующих случаях:

- невозможно организовать обратный канал, либо время распространения сигнала по каналу очень велико ( связь с дальними космическими станциями);

- высокая вероятность ошибки Р₀ в канале при слабом их группировании

( системы с ОС большую часть времени находятся в режиме повторения).