4.3.1. Декорреляция ошибок в системах пдс

Рассмотрим влияние предположения о независимости ошибок в канале связи.

Изобразим качественную зависимость вероятности появления ошибки кратности m от этой величины.

Рис. 4.4

Отсюда видно, что при независимых ошибках вероятность появления ошибок высокой кратности быстро падает. В реальных же каналах этого явления не происходит, т.е. возникают ошибки высокой кратности – пакеты ошибок.

Для борьбы с этим явлением применяют различные методы рассредоточения е. э. с последующим их группированием на приёмной стороне. Рассмотрим один из методов декорреляции, обладающий максимальной наследностью.

Перед передачей в канал элементы кодовой комбинации записываются в табличном виде:

В данном случае i+1 – число столбцов;

j – число строк. Как правило j=1.

Передача в канал производится по строкам:

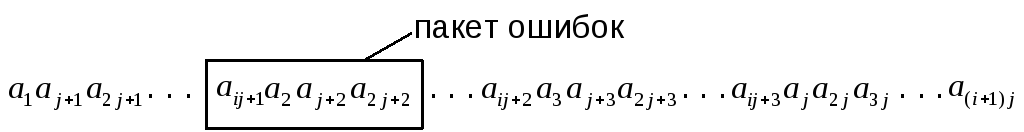и т.д.

На приёме производится обратное преобразование и декодирование производится по столбцам.

В результате пакет ошибок, поражающий кодовую комбинацию, оказывается распределённым, т.е. ошибки разнесены не менее, чем на j единичных элементов.

Существенным недостатком данного способа выступает необходимость ЗУ достаточно большой ёмкости как на передаче, так и на приёме.

Другим методом декорреляции ошибок является использование псевдослучайных последовательностей, т.е. скремблирования. На передаче псевдослучайная комбинация накидывается на передаваемую комбинацию, на приёме происходит обратное преобразование с использованием той же псевдослучайной последовательности. В результате происходят те же процессы, что мы рассматривали в предыдущем методе.

Основным преимуществом данного метода выступает возможность последовательного выполнения процесса декорреляции.

Существуют и другие методы декорреляции ошибок. Применение рассмотренных методов позволяет более эффективно использовать исправляющую способность кодов и, в конечном счёте, повысить эффективность работы систем ПДС без ОС.

4.4. Принципы помехоустойчивого кодирования

Основы теории кодирования были заложены К. Шенноном, соответствующая теорема рассмотрена в 3.1. Однако теорема справедлива лишь для каналов без шума. Рассмотрим основные принципы, положенные в основу помехоустойчивого кодирования.

В первичных (простых, примитивных) кодах используются все N кодовых комбинаций (КК), которые можно получить при построении кода длиной n. Например, если необходимо передать 32 буквы алфавита двоичным кодом (т.е. кодом с основанием m=2), то необходимая длина КК (число разрядов) определяется как:

Любая из 5-ти элементных КК представляет собой какой-то знак алфавита. Если в процессе передачи такой КК произойдет одна ошибка, то принятая КК будет восприниматься приёмником как КК соответствующая другому знаку. Например, буква “Я” – 11101 при искажении 1-го разряда будет принята как буква “У” – 11100.

Таким образом, при передаче сообщений примитивным кодом обнаружение и восстановление ошибочно принятых единичных элеметов невозможно.

Обнаружить ошибку в данном случае может только получатель, за счёт смысловой избыточности текстового сообщения. Кстати, это является одной из причин, по которым на телеграфных сетях общего пользования не применяется помехоустойчивое кодирование, т.к. получатель в данном случае является “оптимальным” декодером.

Коды, у которых все КК разрешены к передаче называются простыми или примитивными первичными.

При избыточном кодировании всё множество КК () разбивается на 2 подмножества:

• подмножество разрешённых КК, обладающих определёнными свойствами–признаками;

• подмножество запрещённых КК , этими признаками не обладающих.

В дискретный канал передаются только разрешённых КК. Если в результате искажений переданная КК переходит в подмножество запрещённых КК, то на приёме ошибка будет обнаружена. Однако, если совокупность ошибок в дискретном канале превращает данную КК в другую разрешённую КК, то в этом случае ошибки не могут быть обнаружены.

Таким образом, идея помехоустойчивого кодирования заключается в том, что в передаваемую КК необходимо внести по определённым правилам избыточность – признаки разрешённой КК. Правила внесения избыточности (признаки) должны быть известны как на передаче, так и на приёме.

Исправление ошибок можно пояснить следующим образом. Множество запрещённых КК разбивается нанепересекающихся подмножеств. (Непересекающимися множествами называются множества, не имеющие ни одного общего элемента).

Каждому из подмножеств ставится в соответствии одна из передаваемых, разрешённых. Способ приёма заключается в следующем. Если принята КК, приписанной, то считается, что передана.

Рассмотрим геометрическую интерпретацию (рис. 4.5).

Здесь - - множество разрешённых (передаваемых) КК;

- множество всех возможных запрещённых КК, в которые могут перейти разрешённые КК из множества ;

-подмножества, на

которые разбиты запрещённые КК.

Рис. 4.5

Способ приёма состоит в следующем. Если приняты КК - ,или(принадлежащие к), то считается, что передавалась КК -. Если действительно КК -,илиобразовалась из, то ошибка исправлена. Если принятая КК переходит в другое подмножество, например,, то принимается ошибочное решение, что передавалась КК -.

Очевидно, что способность исправлять ошибки зависит от способа разбиения на подмножества , т.е. от способа кодирования и декодирования. В свою очередь способ кодирования зависит от характера ошибок в дискретном канале связи.