
Контрольная работа по ОТМО
.docТеоретические сведения
Простейший поток
Если поток требований обладает свойством стационарности, ординарности и отсутствием последействия, то такой поток называется простейшим.
Вероятность поступления k требований за промежуток времени t в пуассоновском потоке определяется из выражения:
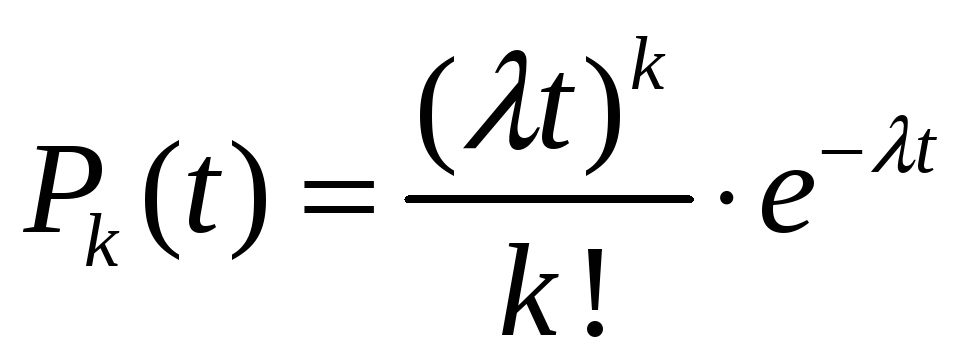
Интервал времени Т между двумя соседними событиями простейшего потока имеет показательное распределение:
![]()
где
![]() -
величина обратная среднему значению
интервала Т.
Математическое ожидание (М), дисперсия
(D)
и среднеквадратическое отклонение (σ)
промежутка Т
равны:
-
величина обратная среднему значению
интервала Т.
Математическое ожидание (М), дисперсия
(D)
и среднеквадратическое отклонение (σ)
промежутка Т
равны:
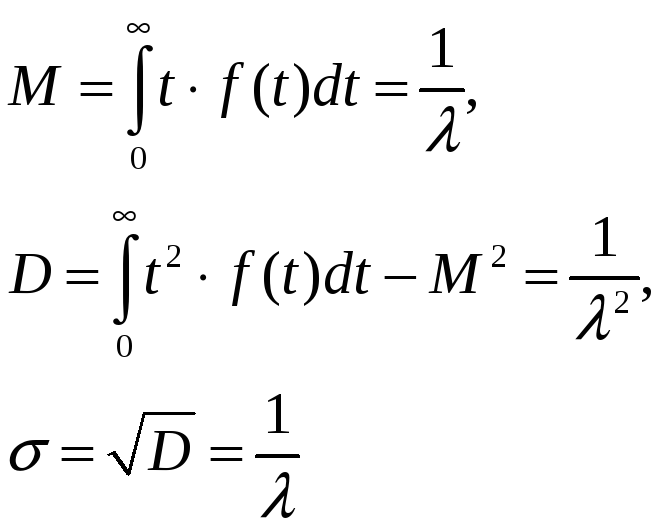
Полученное
совпадение величин М
и
![]() характерно для показательного
распределения.
Это свойство на практике используют
как критерий для первоначальной проверки
соответствия гипотезы о показательном
распределении, полученном по статистическим
данным.
характерно для показательного
распределения.
Это свойство на практике используют
как критерий для первоначальной проверки
соответствия гипотезы о показательном
распределении, полученном по статистическим
данным.
Рассмотрим пример. По шоссе мимо наблюдателя движется в одном направлении простейший поток автомобилей. Известно, что вероятность отсутствия машин в течении 5 минут, равно 0,5. Необходимо вычислить вероятность того, что за 10 минут мимо наблюдателя пройдет не более двух машин.
Для того, чтобы решить эту задачу, примем:
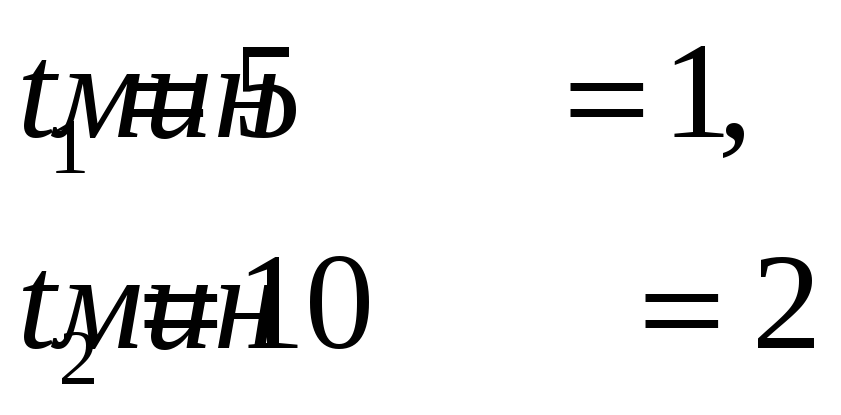
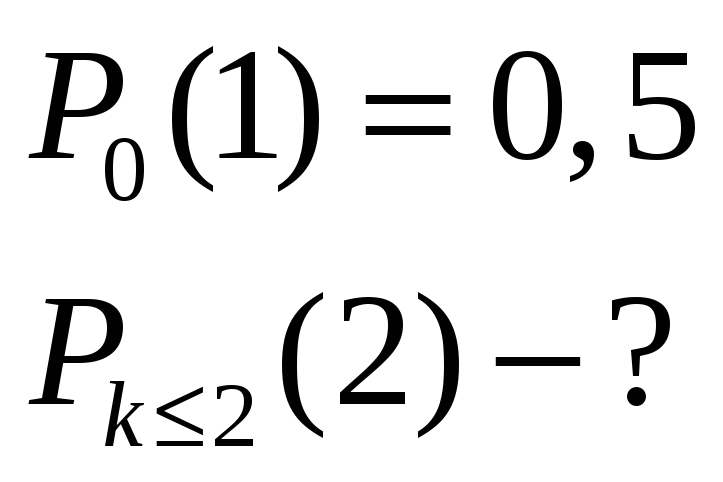
Найдем интенсивность потока автомобилей, используя известную нам вероятность отсутствия автомобилей за 5 минут:

Теперь мы можем вычислить необходимую нам вероятность:
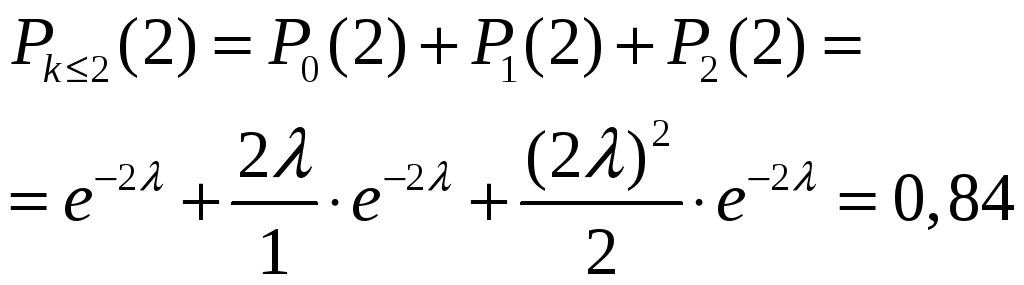
Суммирование и разъединение простейших потоков
При
объединении нескольких независимых
простейших потоков образуется также
простейший поток с параметрами, равными
сумме параметров исходных потоков. При
разъединении на n
направлений так, что каждое требование
исходного потока с вероятностью рi
поступает
на i-oe
направление поток i-oго
направления
будет также простейшим с параметром
![]() pi.
pi.
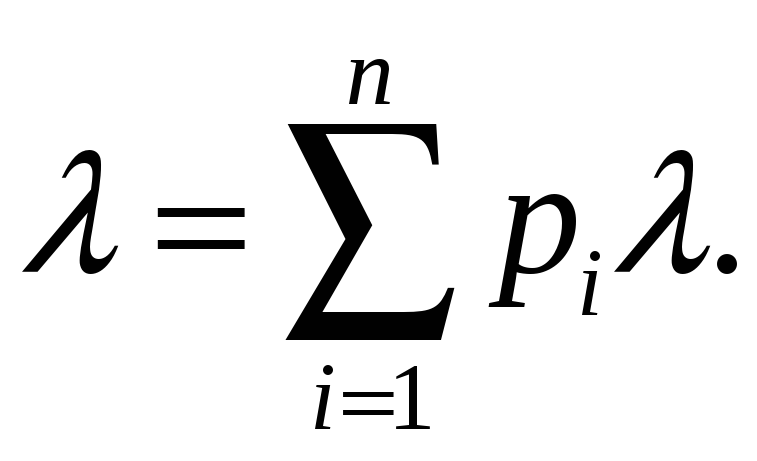
Эти свойства простейшего потока широко используются на практике, так как значительно упрощают расчёты стационарного оборудования и информационных сетей.
Рассмотрим пример. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 4 машины в минуту. Шоссе имеет развилку в два направления. Вероятность движения машин в первом направлении 0,12, во втором – 0,88. Определить интенсивности в обоих направлениях.
Решение.
![]() =4
[1/мин]
=4
[1/мин]
P1(t)=0,12
P2(t)=0,88
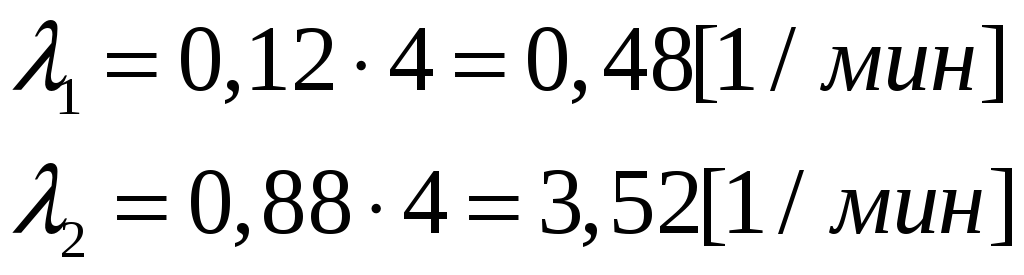
Теорема Литтла
Среднее число требований в системе N и среднее время пребывания в системе Т связаны между собой представленным соотношением:
![]() ,
,
где
![]() -
средняя скорость поступления требований
в систему.
-
средняя скорость поступления требований
в систему.
Рассмотрим
пример.
В три узла сети связи поступают пакеты
с интенсивностями
![]() =100
пак/сек,
=100
пак/сек,
![]() =200
пак/сек,
=200
пак/сек,
![]() =252
пак/сек. Определить среднюю задержку
пакета в сети, если общее число пакетов
внутри сети 1618.
=252
пак/сек. Определить среднюю задержку
пакета в сети, если общее число пакетов
внутри сети 1618.
![]()
Т=1618/(100+200+252)=2,93 сек
Задание на контрольную работу
Задача 1. В справочную службу поступает простейший поток телефонных вызовов. Известно, что вероятность отсутствия вызовов в течении t1 минут, равно 0,5. Необходимо вычислить вероятность того, что за t2 минут поступит не более n вызовов.
Задача 2. Пакеты, поступающие на маршрутизатор, представляют собой простейший поток с интенсивностью λ пакета в минуту. Маршрутизатор распределяет пакеты по двум направлениям. Вероятность маршрутизации пакетов в первом направлении p1, во втором – p2. Определить интенсивности в обоих направлениях.
Задача
3.
В узел сети связи поступают пакеты с
интенсивностью
![]() =100
пак/сек., Определить общее число пакетов
внутри узла сети, если средняя задержка
пакета равна T
секунды.
=100
пак/сек., Определить общее число пакетов
внутри узла сети, если средняя задержка
пакета равна T
секунды.
Все необходимые исходные данные для выполнения контрольной работы по вариантам, где m – последняя цифра номера зачетной книжки, представлены в таблице 1.
Таблица 1
|
Параметр/m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
t1 |
2 |
5 |
3 |
1 |
2 |
5 |
6 |
4 |
1 |
10 |
|
t2 |
6 |
20 |
6 |
4 |
4 |
15 |
12 |
8 |
2 |
20 |
|
n |
2 |
3 |
4 |
5 |
1 |
3 |
4 |
5 |
2 |
1 |
|
λ |
20 |
10 |
15 |
5 |
3 |
35 |
16 |
14 |
8 |
7 |
|
p1 |
0.55 |
0.7 |
0.35 |
0.25 |
0.4 |
0.85 |
0.63 |
0.41 |
0.72 |
0.9 |
|
p2 |
0.45 |
0.3 |
0.65 |
0.75 |
0.6 |
0.15 |
0.37 |
0.59 |
0.28 |
0.1 |
|
T |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
0.5 |
0.7 |
0.6 |
0.8 |
