Вопр_гос_эк_ЭД и РРВ / Особенности распр_ СВЧ волн в атмосфере

Особенности распространения СВЧ электромагнитных волн в атмосфере, рефракция

волн и поглощение

В качестве примера рассмотрим высокочастотную дисперсию диэлектрической проницаемости одноатомного газа. Согласно классической модели атома, электроны в нем совершают гармонические колебания относительно ядра. Рассмотрим атом, как гармонический осциллятор, в котором смещение электрона под действием переменного во времени электрического поля волны описывается уравнением

.

Здесь  частота собственный колебаний электрона, находящегося на соответствующей оболочке молекулы газа,  эффективный коэффициент затухания, который обратно пропорционален времени жизни возбужденного состояния атома. Вынужденное решение этого уравнения имеет вид

.

Поляризацию среды характеризует дипольный момент единичного объема здесь  дипольный момент атома,  концентрация электронов на оболочке молекулы газа. Учитывая связь между значениями векторов индукции , поляризации и напряженности электрического поля в однородном изотропном диэлектрике

и ,

приходим к выражению для относительной диэлектрической проницаемости газа

.

Мы видим, что классическая модель атома приводит к зависимости , которая характеризует дисперсию среды, которую необходимо учитывать на частотах, близких к резонансным частотам соответствующих электронных оболочек .

Мы видим также, что диэлектрическая проницаемость газа является комплексной. Рассмотрим физический смысл этого явления. Введем комплексный показатель преломления

.

Здесь мы считали, что поправка диэлектрической проницаемость, вызванная колебаниями электронов во внешнем переменном полей, много меньше единицы и воспользовались соотношением . Далее, разделяя действительную и мнимую части показателя преломления, получим

,

.

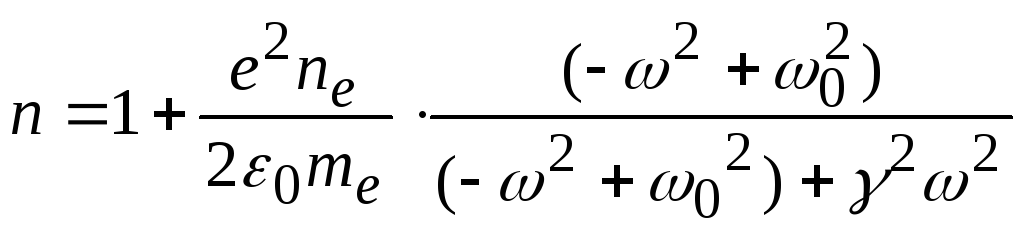Зависимости и показаны на рисунке. Мы видим, что функция напоминает резонансную характеристику колебательного контура, возрастая вблизи частоты . Действительная часто показателя преломления имеет излом вблизи частоты . При показатель преломления увеличивается с ростом частоты, в этом случае и фазовая скорость волны уменьшается с ростом (имеет место так называемая нормальная дисперсия). В близи частоты существует достаточно узкая область, где и имеет место возрастание фазовой скорости (область аномальной дисперсии). Подставляя показатель преломления в выражение для электрического поля плоской волны, получим

,

где  фазовая скорость,  коэффициент затухания, который определяет характерный масштаб , на котором амплитуда волны убывает в раз. Рассмотрим единицы, в которых обычно измеряется поглощение. Ими являются непер (Нп) и децибел (дБ), которые определяются следующим образом. Децибел равен десяти бела, который в свою очередь равен десятичному логарифму отношения интенсивностей и радиоволн в точках, разнесенных друг относительно друга на некоторое расстояние, например км. В этом случае говорят, что поглощение составляет

(дБ/км).

В основу определения непера положен натуральный логарифм , поэтому НпдБ, где  основание натурального логарифма.