
- •Волжская государственная академия водного транспорта
- •Основные понятия из линейной алгебры и дифференциального исчисления.
- •В. Даль «Толковый словарь…» матричная азбука Основные определения и обозначения
- •Действия с матрицами
- •Определители матриц.
- •Таким образом, по определению для любого натурального n имеем
- •Свойства определителей
- •Обратная матрица
- •Ранг матрицы.
- •Решение систем
- •I. Метод обратной матрицы.
- •II. Правило Крамера.
- •III. Метод Гаусса
- •Векторная азбука Основные определение и обозначения
- •Линейные действия с векторами.
- •Базис и координаты.
- •Система координат «точечного» пространства.
- •Задача о делении отрезка в данном отношении.
- •Правило вычисления векторного произведения
- •Основные приложения векторного произведения
- •Смешанное произведение векторов.
- •Азы аналитической геометрии. Уравнения прямой на плоскости.
- •Угол между прямыми.
- •Расстояние от точки до прямой.
- •Уравнения плоскости в пространстве.
- •Расстояние от точки до плоскости.
- •Уравнение прямой в пространстве.
- •Параметрические уравнения прямой –
- •Канонические уравнения прямой
- •Расстояние от точки до прямой
- •Замечания о взаимном расположении.
- •Кривые второго порядка.
- •Азбука дифференциального исчисления. Переменные величины.
- •Предел переменной
- •«Монотонная и ограниченная последовательность имеет предел»
- •Характеристический признак существования предела.
- •Сравнение бесконечно малых переменных величин.
- •Характеристическое свойство бесконечно малых
- •Непрерывность.
- •Асимптоты функции
- •Свойства непрерывных функций
- •Производные фоункции
- •Правило дифференцирования сложной функции
- •Дифференциал функции.
- •Арифметические свойства дифференциала
- •Производные и дифференциалы высших порядков.
- •Приложения производных к исследованию функций.
- •Азы дифференциального исчисления функции нескольких переменных. Основные определения
- •Производные функции многих переменных.
- •Дифференцирование неявных функций
- •Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности.
- •Старшие производные
- •Экстремумы функций двух переменных.
- •Векторная функция скалярного аргумента
- •Задания к контрольной работе № 1
- •Задания на контрольную работу № 2
- •Литература
Волжская государственная академия водного транспорта
Кафедра математики
В.Н. Белых, Я.Н. Сенниковский
Основные понятия из линейной алгебры и дифференциального исчисления.
Методические указания для студентов заочного обучения
технических специальностей
Н. Новгород
1999
Настоящее пособие адресовано студентам всех специальностей заочного обучения. Оно призвано помочь им в освоении необходимого минимума теоретического материала и привить определенные навыки для решения задач контрольной работы № 1 и № 2. Подготовить к сдаче зачета и экзамена по темам: «Решение систем линейных уравнений», «Основы векторной алгебры и аналитической геометрии» и «основные понятия дифференциального исчисления». Изложены основные понятия приведены примеры решения задач и даны задания для выполнения контрольной работы № 1 и № 2.
Азбука…собрание в порядок…какой либо грамоты,…учебник грамоты, букварь: начальные основания какой- либо науки… Азбука наука, а ребятам бука (мука)…
В. Даль «Толковый словарь…» матричная азбука Основные определения и обозначения
Матрицей размерами "m на n" или коротко, (m x n) - матрицей называется таблица из m строк и n столбцов, элементами которой могут быть числа, буквы, вектора, матрицы, а также любые математические выражения, составленные из них. Изображают матрицу как обведенную круглыми скобками таблицу
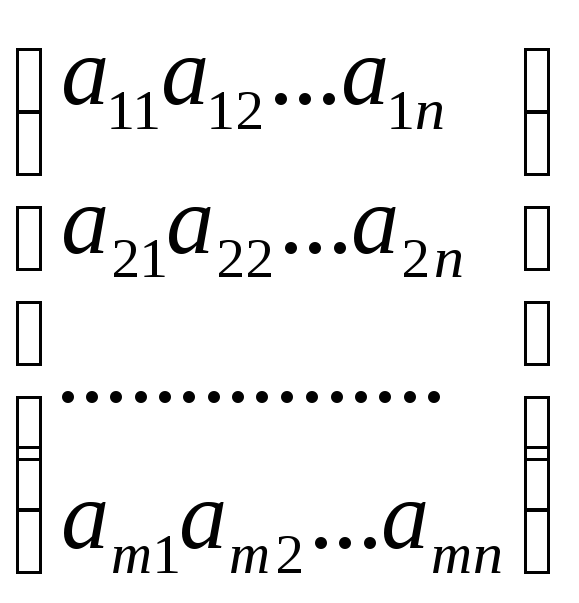
а обозначают заглавными буквами латинского или русского алфавита - А, В, С, D и т.д. Элементы матриц, как видно из ее изображения, обозначают соответствующими малыми буквами аij, bij¸ … где i указывает номер строки, а j - номер столбца, в которых этот элемент находится.
Действия с матрицами
1. Матрица размерами "n на m" называется транспонированной по отношению к данной (m x n) – матрице если каждая е строка является соответствующим столбцом данной. Обозначают такие «взаимно транспонированные» матрицы одной и той же буквой, добавляя к одной из них верхний индекс «т», например: А и АТ, ВТ и В и т.д.
Примеры:
В
=
![]() ;
ВТ
= (2 1 0); С =
;
ВТ
= (2 1 0); С =
 ;
СТ
=
;
СТ
=
![]() .
.
II. Суммой двух матриц одинаковых размерностей, например А и В, называется новая матрица С тех же размеров элементы которой
сij = аij + bij
III. Произведениемматрицы А на число λ называется матрица В элементы которой
bij = λ aij
Действия II. и III. Называют линейными действиями с матрицами, а выражения типа "αА + βВ" - линейными комбинациями матриц.
Пример
2 ·
 + 3 ·
+ 3 · =
=
IY. Произведением ( 1 х n ) - матрицы строки на ( n х 1 ) - матрицу столбец называется (1х1) - матрица единственный элемент которой
с
1 1 =
![]()
Пример
(1 -1 3) ·
![]() = (2 – 5 – 6) = (-9).
= (2 – 5 – 6) = (-9).
Y. Произведением (m х n) - матрицы А на (n х p) - матрицу В называется (m х р) - матрица С Элементами которой является элементы (1 х 1) – матриц, образующихся при перемножении i – ой стройки А на j – ый столбец В. Таким образом
сij
=
![]()
Примеры 1)
![]() · (10 -11) =
· (10 -11) = ;
;
2)
 ·
·![]() =
= ;
;
3)
![]() ·
·![]() =
=
Особую
роль при перемножении играет так
называемая единичная (
![]() ) – матрица Е, элементы которой
) – матрица Е, элементы которой

Как и числовая единицы, эта матрица при умножении (если это допустимо) на любую другую не изменяет последнюю. Например
А
· Е =
 ·
·![]() =
= = А
= А
