
u_p_empp
.pdf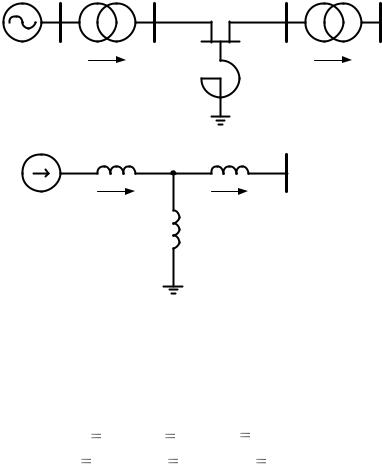
1.5.2. Влияние шунтирующего реактора
Шунтирующие реакторы (ШР) используются в высоковольтных электрических сетях для компенсации избыточной реактивной мощности, генерируемой линиями электропередачи. Реакторы подключаются наглухо или через выключатели в концевых точках линий электропередачи длиной свыше 300 км для предотвращения появления перенапряжений при коммутационных переключениях. В некоторых случаях реакторы подключаются к шинам высшего напряжения станционных и сетевых подстанций.
Подключение ШР в промежуточной точке электрической связи одномашинной энергосистемы (рис. 1.12,а) вносит дополнительное индуктивное сопротивление в схему замещения (рис. 1.12,б), что отража-
ется на обобщенных параметрах Z11 , Z22 |
и Z12 . |
|
|||
Г |
|
Т1 |
Л1 |
Л2 |
Т2 U |
а |
|
|
|
|
|
|
|
PГ |
ШР |
|
PН |
|
|
|
|
|
|
|
Еq |
x1 |
|
x2 |
U |
|
|
|
|
||
б |
|
|
|
|
|
|
|
PГ |
|
PН |
|
|
|
|
xL |
|
|
Рис. 1.12. Энергосистема с ШР в промежуточной точке ЛЭП (а) и схема еѐ замещения (б)
В принятой идеализации схем замещения элементов обобщенные параметры, как и исходные для их расчета сопротивления, не содержат вещественных частей:
Z1 |
jx1; Z2 |
jx2 ; Z3 |
jxL ; |
|
Z11 |
jx11; Z22 |
jx22 ; Z12 |
jx12 . |
(1.72) |
Поэтому дополняющие углы α11 , α22 и α12 равны нулю, а зависимости РГ (δ) , РН (δ) совпадают и выражаются одной формулой
31
|
|
|
|
РГ (δ) |
РН (δ) |
Рм sin δ . |
|
(1.73) |
||
|
Рассмотрим случаи, когда ШР отключен и когда он находится в |
|||||||||
работе. |
|
|
|
|
|
|
|
|
|
|
|
В первом случае взаимное сопротивление Z12 |
и соответствующий |
||||||||
предел мощности Рм определяется как: |
|
|
|
|||||||
|
|
|
|
Z12 |
jx12 |
jx1 |
jx2 ; |
|
(1.74) |
|
|
|
|
|
Рм |
EU |
x12 . |
|
|
|
|
|
Во втором случае на аналогичные параметры Z12 , Рм |
оказывает |
||||||||
влияние индуктивное сопротивление реактора xL , что выражается в ви- |
||||||||||
де: |
|
|
|
|
|
|
|
|
|
|
|
|
Z12 |
jx12 |
jx1 |
jx2 |
jx1 jx2 |
j(x12 |
xL ) ; |
(1.75) |
|
|
|
|
jxL |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рм |
EU x12 |
EU (x12 |
xL ) , |
|
(1.76) |
||
где |
xL |
x1x2 xL |
0 . |
|
|
|
|
|
|
|
|
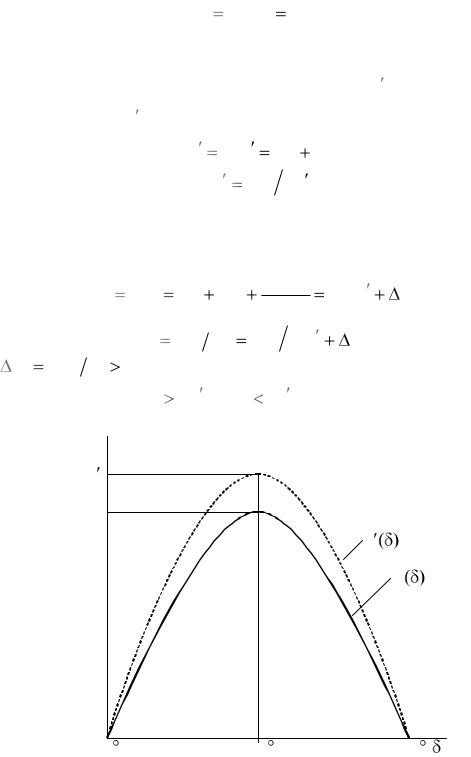
Очевидно, что x12 |
x12 |
и Рм |
Рм (рис. 1.13). |
|
|
||||
|
|
P |
|
|
|
|
|
|
|
|
|
|
Pм |
|
|
|
|
|
|
|
|
|
|
Pм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
0 |
|
|
|
90 |
|
|
180 |
|
Рис. 1.13. Влияние ШР на угловую характеристику мощности генератора |
||||||||||
Из этого следует, что шунтирующий реактор, подключенный в промежуточной точке линии электропередачи, оказывает отрицательное влияние на статическую устойчивость одномашинной энергосистемы.
32
1.5.3. Влияние конденсаторной батареи
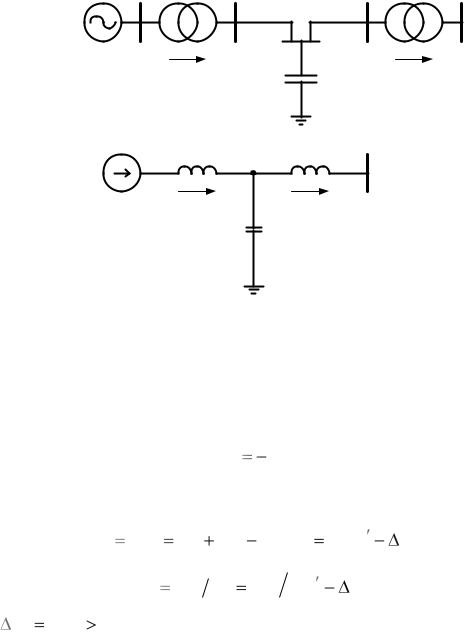
Конденсаторные батареи (КБ) иногда устанавливаются и подключаются в промежуточных точках линий электропередачи с целью поддержания нормальных уровней напряжения при передаче больших потоков мощности. Оценим влияние КБ на статическую устойчивость одномашинной энергосистемы при таких же расчетных условиях, что и в предыдущих случаях (рис. 1.14, а, б).
Г |
|
Т1 |
Л1 |
Л2 |
Т2 U |
а |
|
|
|
|
|
|
|
PГ |
КБ |
|
PН |
|
|
|
|
|
|
|
Еq |
x1 |
|
x2 |
U |
|
|
|
|
||
б |
|
|
|
|
|
|
|
PГ |
|
PН |
|
|
|
|
xC |
|
|
Рис. 1.14. Энергосистема с КБ в промежуточной точке ЛЭП (а) и схема еѐ замещения (б)
При подключенной КБ в схеме замещения энергосистемы (рис. 1.14, б) появляется элемент с отрицательным реактивным сопротивлением
|
|
|
Z3 |
|
jxC , |
|
|
|
(1.77) |
|
влияние которого на взаимное сопротивление |
Z12 |
и предел мощности |
||||||||
определяется по выражениям: |
|
|
|
|
|
|
|
|||
|
|
Z12 jx12 |
jx1 jx2 |
|
jx1 jx2 |
|
j(x12 |
xC ) ; |
(1.78) |
|
|
|
|
jxC |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
Рм |
EU x12 |
EU (x12 |
|
xC ), |
|
(1.79) |
||
где xС |
x1x2 |
0 . |
|
|
|
|
|
|
|
|
xC |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
33
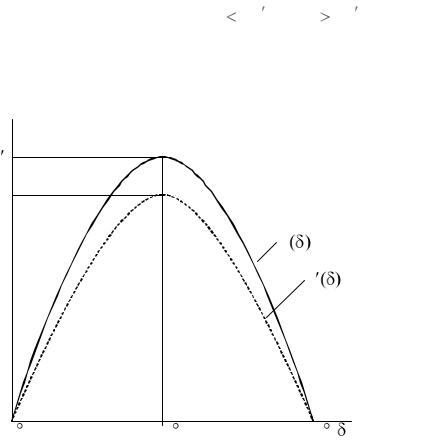
Из этих соотношений видно, что x12 x12 и Рм Рм (рис. 1.15),
то есть конденсаторная батарея, подключенная в промежуточной точке линии электропередачи, оказывает положительное влияние на статическую устойчивость одномашинной энергосистемы.
P |
|
|
Pм |
|
|
Pм |
|
|
|
|
P |
|
|
P |
0 |
90 |
180 |
Рис. 1.15. Влияние КБ на угловую характеристику мощности генератора
Следует отметить, что выводы, касающиеся влияния шунтирующих реакторов и конденсаторных батарей на статическую устойчивость распространяются и на сложные энергосистемы.
1.6. МЕТОД МАЛЫХ КОЛЕБАНИЙ ДЛЯ АНАЛИЗА СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ЭНЕРГОСИСТЕМ
1.6.1. Линеаризация уравнений и ее назначение
Распространенным способом упрощения нелинейных дифференциальных уравнений, описывающих электромеханические переходные процессы электроэнергетических систем, является линеаризация этих уравнений. Различают линеаризацию «в большом» и линеаризацию
«в малом».
При линеаризации «в большом» нелинейная зависимость заменяется кусочно-линейной. Например, синусоида представляется в виде трапеции (рис. 1.16). Существуют определенные способы и критерии
34
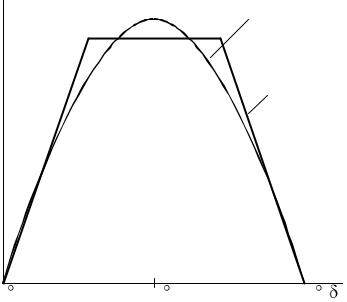
линеаризации, благодаря которым кусочно-линейная зависимость наи- |
||
более близко отображает исходную функцию. |
|
|
P |
|
Исходная |
|
|
функция |
|
|
Линейная |
|
|
функция |
0 |
90 |
180 |
Рис. 1.16. Кусочно-линейное представление синусоидальной зависимости |
||
Линеаризация «в большом» больше применима для анализа динамичной устойчивости энергосистем и используется, в основном, для исследовательских целей.
Линеаризация «в малом» представляет собой замену исходной нелинейной функции линейной зависимостью на малом или бесконечно малом линейном отрезке в окрестности какой-либо точки функции. При анализе статической устойчивости энергосистем такой точкой, как правило, является точка, изображающая исследуемый установившийся режим.
Метод исследования статической устойчивости энергосистем, опирающийся на линеаризацию «в малом», называется методом малых колебаний. При этом под малыми колебаниями подразумеваются изменения малых линейных приращений параметров режима энергосистемы в окрестности точки, изображающей исследуемый установившийся режим. Численные значения параметров этого режима рассматриваются в качестве координат изображающей точки в многомерном пространстве.
Для полной характеристики малых колебаний параметров режима требуется получение частных решений системы линейных дифференциальных уравнений, получаемых в результате линеаризации «в малом». Однако, как доказал известный русский математик А.М. Ляпунов, для
35
суждения об устойчивости системы нет необходимости исследовать частные решения. Можно ограничиться рассмотрением так называемых свободных колебаний параметров режима, получаемых в виде общих решений систем линеаризованных дифференциальных уравнений.
По общему решению системы линейных дифференциальных уравнений можно определить тенденцию к развитию процессов. Если оказывается, что малые приращения параметров режима самопроизвольно (при отсутствии возмущающих воздействий на систему) не возрастают, то энергосистема работает в устойчивом режиме. Если же эти приращения имеют тенденцию к возрастанию, то режим системы неустойчив.
Из общей характеристики метода малых колебаний следует, что при его применении необходимо выполнить следующие действия:
-провести расчет установившегося режима и таким образом определить координаты изображающей точки;
-составить систему дифференциальных и алгебраических уравнений, описывающих электромеханические процессы;
-провести линеаризацию «в малом» дифференциальных и алгебраических уравнений;
-составить характеристическое уравнение полученной системы дифференциальных и алгебраических уравнений и определить его корни;
-по виду корней характеристического уравнения определить тенденцию развития процессов в электроэнергетической системе и сделать заключение об устойчивости (или неустойчивости) исследуемого установившегося режима.
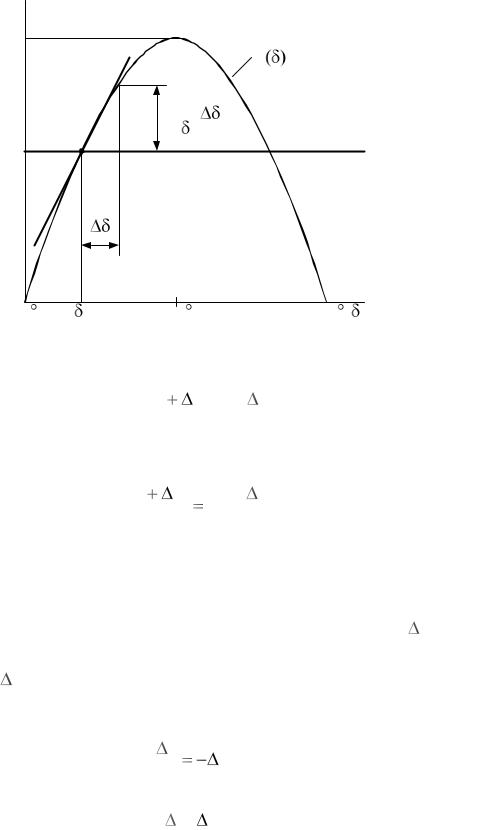
Рассмотрим эти действия на примере исследования статической устойчивости одномашинной нерегулируемой энергосистемы, угловая характеристика генератора которой (рис. 1.17) построена по выражению
P Рм sin δ . |
(1.80) |
Предположим, что исследуемый устанавливающийся режим энер- |
|
госистемы рассчитан, координаты (Р0 ,δ0 ) |
изображающей точки a |
(рис. 1.17) соответственно определены, а электромеханические переходные процессы описываются системой, представленной дифференциальным и алгебраическим управлениями:
d 2δ
Tj dt2 Р0 Р; (1.81)
P Рм sin δ.
36
P |
|
|
|
Pм |
|
|
|
|
|
|
P |
|
|
dP |
|
|
a |
d |
PТ |
P0 |
|
||
|
|
|
|
0 |
0 |
90 |
180 |
Рис. 1.17. Линеаризация |
угловой |
характеристики мощности в |
|
изображающей точке исследуемого режима |
|||
Представим угол δ как δ=δ0 |
δ , где δ – малое приращение уг- |
ла в окрестности точки a , и преобразуем левую часть дифференциального уравнения системы (1.81) с учетом этого равенства, приведя ее к виду
Tj |
d 2 (δ0 |
δ) |
Tj |
d 2 |
δ |
. |
(1.82) |
dt2 |
|
dt2 |
|
Из последнего равенства следует, что при линеаризации второй производной «в малом», достаточно дифференцируемую функцию заменить ее малым линейным приращением. Это же справедливо для производных по времени любого порядка.
В правой части рассматриваемого уравнения приращение |
P0 по- |
|||
стоянной величины P0 равно нулю, |
а приращение переменной |
P обо- |
||
значается как P . |
|
|
||
С учетом этих замечаний в результате линеаризации «в малом» |
||||
первого уравнения системы (1.81) получим линейное уравнение |
|
|||
Tj |
d 2 δ |
P , |
(1.83) |
|
dt2 |
|
|||
в котором в качестве переменных выступают не параметры режима Р,δ , а их малые линейные приращения Р, δ .
37

При линеаризации второго уравнения системы (1.81) следует не-
линейную зависимость P(δ) заменить линейной зависимостью |
P( δ) |
||||||||||||||||||
в окрестности точки a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представим P(δ) как |
P(δ0 |
|
|
|
|
δ) |
и разложим в общем виде эту |
||||||||||||
функцию в ряд Тейлора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(δ0 |
|
δ)=P(δ0 ) |
dP |
|
δ |
|
1 d 2P |
δ2 ... |
(1.84) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dδ |
|
|
2! dδ2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Ограничимся рассмотрением линейной части этого ряда, из кото- |
|||||||||||||||||||
рой вычтем значение функции P(δ0 )=P0 |
в точке a . В результате полу- |
||||||||||||||||||
чим искомую зависимость |
P( |
δ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P |
P(δ |
|
δ) |
P(δ |
|
) |
P(δ |
|
) |
dP |
δ P |
(1.85) |
|||||||
0 |
0 |
0 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dδ |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
dP |
δ . |
|
|
|
|
|
|
(1.86) |
|||||
|
|
|
|
|
|
dδ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отметим, что производная dP dδ представлена в уравнении (1.86)
dδ представлена в уравнении (1.86)
своим численным значением в точке a и поэтому выступает здесь не как функция dP dδ , δ=δ0 , а как коэффициент линейной зависимости
dδ , δ=δ0 , а как коэффициент линейной зависимости
P( δ) .
Линейная зависимость вида (1.86) может быть получена и без предварительного разложения линеаризуемой функции в ряд Тейлора. Эта зависимость полностью соответствует формулам записи полного дифференциала функции, что позволяет формализовать и тем самым упростить операции по линеаризации «в малом». Особенно это важно при линеаризации функций нескольких переменных, которая, как и получение полного дифференциала, производится с использованием частных производных. Например, линеаризация «в малом» некоторой функции z(x,y) в общем виде осуществляется по формуле получения полного дифференциала этой функции:
|
z |
|
dz |
x |
dz |
y . |
(1.87) |
|||||
|
|
|
|
|
|
|||||||
|
|
dx |
dy |
|||||||||
Уравнения (1.83, 1.86) образуют искомую систему, которая при |
||||||||||||
исключении переменной |
P приводится к одному уравнению |
|
||||||||||
|
Tj |
d 2 δ |
|
|
dP |
|
δ |
0. |
(1.88) |
|||
|
|
dt2 |
|
dδ |
||||||||
Этим уравнением описываются свободные колебания малого ли- |
||||||||||||
нейного приращения δ |
угла δ ротора генератора в окрестности рас- |
|||||||||||
сматриваемой точки a (см. рис 1.17). |
|
|
|
|
||||||||
38
1.6.2. Анализ статической устойчивости одномашинной энергосистемы
Для выявления тенденции изменения переменной δ рассмотрим
варианты общего решения уравнения (1.88) |
|
||||||||||
δ(t) |
C e p1t |
C e p2t , |
(1.89) |
||||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
где C1 , C2 – произвольные постоянные, а p1 , |
p2 – корни характеристи- |
||||||||||
ческого уравнения |
|
|
|
|
|
|
|
|
|
|
|
Tj |
p2 |
|
dP |
0 , |
|
|
(1.90) |
||||
|
|
|
|
|
|
|
|||||
|
dδ |
||||||||||
|
|
|
|
|
|
|
|
||||
определяемые как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
1 |
|
dP |
. |
(1.91) |
||
|
|
|
|
|
|
||||||
1,2 |
|
|
|
|
Tj |
|
dδ |
|
|||
|
|
|
|
|
|
|
|||||
В случае, когда dP dδ 0 корни |
|
p1,2 |
α – вещественные, и об- |
||||||||
щее решение (1.89) представляет собой сумму двух экспоненциальных составляющих:
δ(t) C eαt |
C e-αt . |
(1.92) |
1 |
2 |
|
Как видно, с течением времени t |
составляющая C eαt |
возрастает, |
|
1 |
|
а составляющая C2e-αt убывает (рис.1.18).
|
|
C1e t |
|
C2 |
|
|
|
|
|
C2e t |
|
C1 |
|
|
|
0 |
|
|
|
|
t |
||
Рис. 1.18. Составляющие решения (1.92) уравнения (1.88) |
|||
В целом же малое приращение |
δ угла δ имеет тенденцию к воз- |
||
растанию, что является признаком неустойчивости энергосистемы. При этом нарушение устойчивости, то есть переход ротора генератора в асинхронный режим по отношению к генераторам приемной энергосис-
39
темы, происходит в виде «сползания» без периодических изменений угла.
Этот вид нарушения статической устойчивости называется апе-
риодическим или неустойчивостью по «сползанию». |
|
|||
При dP dδ 0 корни |
p1,2 |
jν – мнимые сопряженные, и общее |
||
решение (1.89) представляется в виде |
|
|
||
δ(t) |
C e jνt |
C e jνt . |
(1.93) |
|
|
|
1 |
2 |
|
В этом случае произвольные постоянные C1 и C2 |
является ком- |
|||
плексно-сопряженными величинами, то есть |
|
|||
C1 |
A |
jB ; C2 |
A jB . |
(1.94) |
С учетом (1.94) на основе известного преобразования Эйлера решение (1.93) может быть представлено в виде двух гармонических составляющих:
|
|
|
|
δ(t) ( A jB)e jνt |
( A jB)e jνt |
|
||||||||||||
|
|
|
|
A(e jνt |
|
e |
|
jνt ) |
B |
(e jνt |
|
e jνt ) |
|
(1.95) |
||||
|
|
|
|
|
|
|
|
|
j |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Acos νt |
|
2Bsin νt. |
|
|
|
|
|
|||||||
|
Сделаем замену A |
cos |
|
, B |
|
sin |
и преобразуем решение (1.95) |
|||||||||||
к более удобному для анализа виду |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
δ(t) 2C(cos νt cos |
sin νt sin |
) |
(1.96) |
|||||||||||
|
|
|
|
2C cos(νt |
|
), |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
B |
|
|
|
|
|
|
|
|||||||
|
|
|
|
arctg |
|
|
|
|
1 dP |
|
|
|
|
|||||
где C |
|
A2 B2 , |
, |
ν |
|
– частота свободных колеба- |
||||||||||||
|
A |
|
|
Tj |
|
dδ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ний линейного приращения угла.
Из (1.96) следует, что изменение малого линейного приращения угла происходит по закону незатухающих гармонических колебаний с постоянной амплитудой (рис.1.19). Это свидетельствует об устойчивости исследуемого установившегося режима, так как отсутствует тенденция к возрастанию амплитуды свободных колебаний рассматриваемого параметра режима.
Таким образом, устойчивым режимам энергосистемы соответствует условие dP dδ 0 . Такой же результат был получен ранее на осно-
dδ 0 . Такой же результат был получен ранее на осно-
ве логических рассуждений. Период T возникающих при этом условии свободных колебаний линейного приращения угла определяется как
40
