
ТФКП - методичка
.pdf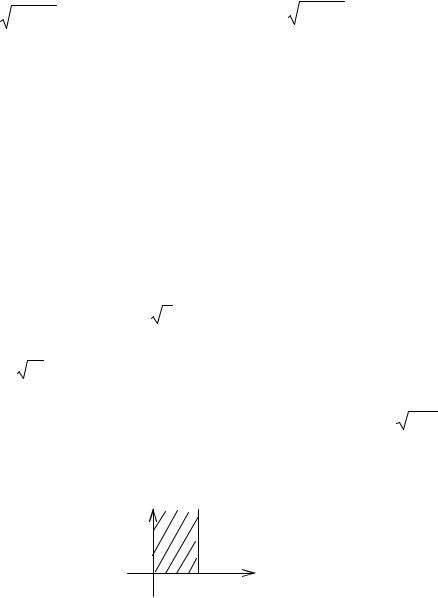
2. ∫ |
|
|
z3 |
|
dz |
(D : |
|
z −1 |
|
<1.5) |
|
2. ∫ |
z cos |
z |
|
dz (D : |
|
z |
|
> 2) |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z +1 |
|||||||||||||||||||||||||||||||||||
|
|
4 −1 |
|
|||||||||||||||||||||||||||||||||||||
∂D z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∞ xsin 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
(x3 + 5x)sin x dx |
|
||||||||||||||||||||||
3. a) 0∫ |
|
|
|
|
|
|
|
|
dx; |
|
|
|
|
|
|
|
|
3. a) |
−∞∫ |
|
x4 + 4x2 +8 |
; |
||||||||||||||||||
x2 + 4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
dx |
|
|
|
|
|
|
|||||||||||
б) ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
∫ |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a |
2 |
+1) |
|
|
2 |
|
|
|
|
|
|||||||
(4 + x) 1 − x2 |
|
|
|
|
|
1 − x |
|
|||||||||||||||||||||||||||||||||
-1 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольная работа 3 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. Найти образы указанных областей D при данных отображениях: |
||||||||||||||||||||||||||||||||||||||||
1) D ={z : x > 0, y > 0}, w = |
|
z-i |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
z + i |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) D ={z : |
|
z |
|
|
> 3/ 2, x > 0, y > 0}, w = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
z + |
z |
; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3) D ={z : |
|
|
|
|
|
|
|
|
< π/ 2}, w = ez ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Im z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4) D ={z : |
|
|
z |
|
< 9, Re z < 0}, w = z, w(-1)= i (ϕ0 = 0); |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
5) D ={z : |
|
z |
|
[0;∞)}, w = ln z; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
z |
01 |
= −1 − 3i |
, w =10πi , |
z |
02 |
= i, |
w = 5πi . |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
01 |
3 |
|
|
|
|
|
02 |
2 |
|
|
|
|
|
|
|
|
|||||||||
2.Доказать: ctg z = i ctg iz ; Im(sh z)= ch x sin y . Вычислить: ii; 7 i +1.
3.Найти функцию, осуществляющую конформное отображение области D на верхнюю полуплоскость.
Im z
|
|
D |
0 |
• |
• |
|
h Re z |
Вариант 2
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : 0 < Re z <1}, w = |
z −1 |
|
; |
|
|
|
|||||
z + 2 |
1 |
|
1 |
||||||||
|
|
|
|
|
|
||||||
2) D ={z : |
|
z |
|
<1/ 2, 0 < arg z < π/4}, |
w = |
||||||
|
|
||||||||||
|
|
|
z + |
; |
|||||||
|
|
|
|
|
|
|
|
2 |
|
z |
|
3) D ={z : z [0;+∞)}, w = ln z, |
|
||||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
71 |
|
|
|
|

z |
01 |
=1, w |
|
= 4πi; z |
02 |
= −i, w |
|
= |
3πi |
; |
|
||||
|
|
|
|
||||||||||||
|
|
01 |
|
|
|
02 |
2 |
|
|
||||||
4) D ={z :1 < Re z < 2}, w = z2 +1; |
|
|
|||||||||||||
5) D = |
z : |
x2 |
+ |
y2 |
|
|
<1, y > 0 , a >1, w(+ i0)= i, w = z + z2 |
−1 . |
|||||||
|
|
|
|
||||||||||||
|
|
|
|
a2 |
|
a2 −1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
2.Доказать: arth z = 12 ln11 +− zz . Вычислить: (1+i)i; 8 i −1; arccos 2.
3.D ={z : z <1, Im z > 0}; G ={w : Im w > 0}. D f =?→G .
Вариант 3
1. Найти образы указанных областей D при данных отображениях:
1) |
D ={z : 0 < arg z < π/ 4 }, w = |
z |
|
; |
|
|
|
|||||
z-1 |
1 |
|
1 |
|||||||||
|
|
|
|
|
|
|
||||||
2) |
D ={z : |
|
z |
|
<1, π/4 < arg z < π/ 2 }, |
|
w = |
|||||
|
|
|
||||||||||
|
|
|
|
z + |
; |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
z |
|
|
|
|
|
|
|
|
|
|
||||
3) |
D ={z : −π/ 2 < Re z < π/ 2, 0 < Im z < 2 }, w = sin z ; |
|||||||||||
4) |
D ={z : |
|
z |
|
<1, z [0;1]}, w = ln z, w(−1 + 0)= −πi ; |
|||||||
|
|
|||||||||||
5) |
D ={z : |
|
z |
|
= 2, 0 < arg z < π/8 }, |
w = z3 −1. |
|
|||||
2.Доказать: Re(cos(x))= cos x ch y ; Im(ch z)= sh y sin y .
Найти все значения функций: arcctg 3; ln(−i) .
3.D f =?→G ={w : Im w > 0}.
y (z)
2i
x
-2i
Вариант 4
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : |
|
|
z +1 |
|
< 2, Re z > 0}, w = |
z −1 |
|
; |
|
||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
z + 3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) |
|
1 |
< |
|
z |
|
|
1 |
|
|
w = |
1 |
|
|
1 |
||||||||||
|
|
|
|
|
|||||||||||||||||||||
D = z : |
|
|
|
<1, z |
;1 , |
|
z + |
; |
|||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
z |
|||||
3) |
|
|
z |
|
> |
1 |
,0 |
< argz |
< |
р |
|
w = |
1 |
; |
|
||||||||||
|
|
|
|||||||||||||||||||||||
D = z : |
|
|
4 |
4 |
, |
z |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
||

4) D = z : |
x2 |
+ |
y2 |
|
<1, z [−1;1] , a >1, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
a2 |
a2 −1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
w(+i0) = −i , w = z + z2 −1 ; |
|
|
|
|
|
|
|
|
|||||||
5) D ={z : Im z > 0}, w = 3 z, z |
0 |
= i, w = − |
3 |
+ |
i |
. |
|
|
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
0 |
2 |
2 |
|
|
|
|
||
|
|
|
|
|
− sh 2y |
|
|
|
|
1 + i |
|||||
2. Доказать: Im ctg z = |
|
|
|
|
|
|
|
||||||||
|
|
|
|
. Вычислить: arccos(−3) |
; ln |
|
. |
||||||||
|
|
|
|
ch 2y − cos 2x |
|
|
|
|
|
|
1 −i |
||||
3. D ={z : z (− ∞;−2] [4;+∞)}; G ={w: Im w > 0}. D f =?→G .
|
|
|
|
|
|
|
|
|
|
Вариант 5 |
1. Найти образы указанных областей D при данных отображениях: |
||||||||||
1) D ={z : 0 < Re z <1}, w = |
z-1 |
; |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
z-2 |
|
2) D ={z : 0 < Im z < π}, w = ch z ; |
||||||||||
3) D ={z : |
|
|
|
z |
|
|
|
< 9, x < y}, w = z2 ; |
||
|
|
|||||||||
4) D = z : |
|
|
|
z |
|
>1, 3π < arg z < 5π , w = z, w(−1)= i ; |
||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
||||
|
|
|||||||||
5) D ={z : z <1, z [0;1]}, w = ln z, w(-1 + 0)= −рi .
2.Доказать: arctg z = 2i ln ii +− zz = 21i ln11 +− iziz .
Решить уравнение:sin z −cos z = i .
3.D f =?→G ={w : Im w > 0}.
|
|
|
|
(z) |
y |
|
|
|
|
|
|
|
•2i |
|
|
|
|
|
|
|
|
• |
•D •2 |
x |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
Вариант 6 |
|
|
||
1. Найти образы указанных областей D при данных отображениях: |
||||||||
1) D ={z : |
|
z |
|
> 2, π/4 < arg z < 3π/ 4}, |
w = |
1 |
|
1 |
|
|
|||||||
|
|
|
z + |
; |
||||
|
|
|
|
|
|
2 |
|
z |
|
|
|
|
|
|
|||
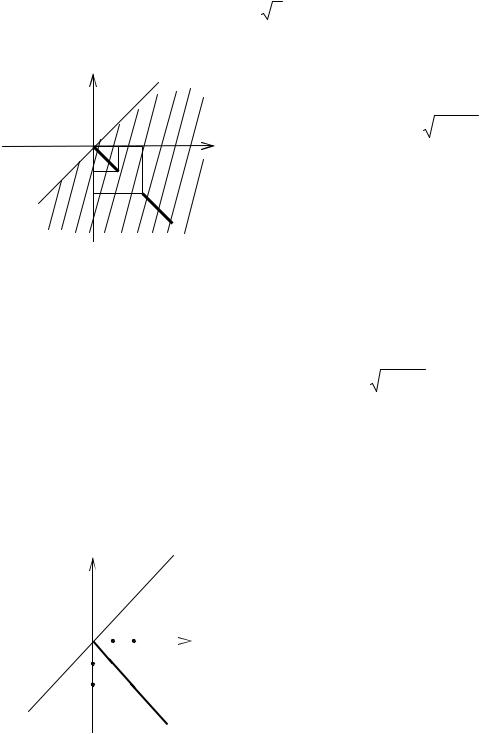
2) D ={z : Re z <1, 0 < Im z < π/ 2}, w = ez ;
3) D ={z : 0 < Re z <1}, w = |
z −1 |
; |
|
z |
|||
|
|
||
|
|
73 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
1 + i |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) D ={z : |
z |
|
<1, Im z > 0}, w = z, w |
|
|
= |
|
|
|
|
; |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5) D ={z : 2 < |
|
z |
|
< 4, z [− 4;−2]}, w = ln z, w(1)= −2πi . |
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
2. Доказать: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin z = −ilni (z + z2 −1). |
|||||||||||||||
|
• |
|
|
|
•1 |
|
|
2• |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
Найти все значения функций: |
|||||||||||||||||||
|
i • |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcctg 2i; ln(cosϕ + isin ϕ), (-π < ϕ≤ π). |
|||||||||||||
|
-2i• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
=? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. D →G ={w : Im w > 0}. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 7 |
|
|
|
|
|
|
|
|
|||||
1. Найти образы указанных областей D при данных отображениях: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) |
D = z : |
z |
|
< 2, π < arg z < |
|
|
π , |
w = |
|
|
|
|
; |
|
|
|
|
|||||||||||||
|
2 |
z − 2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
D = {z :Im z > 0}, w(+ i∞)= 0 , |
w = z + |
|
|
z2 −1 ; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
2 |
|
|
|
i |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3) |
D = z |
: |
z |
<1, |
|
< arg z < |
|
|
π, z 0; |
|
|
|
, |
|
|
w = |
|
z + |
; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
z |
||
|
|
1 |
|
1 |
|
|
|
4) |
D = z :− |
|
< Re z < |
|
, Im z > 0 , |
|
|
2 |
2 |
|
|||||
|
|
|
|
|
|||
w = sin πz ; |
|
|
5) D = {z :a1 < Im z < a2 , a2 − a1 < 2π}, |
||||
|
y |
|
|
|
|||
(z) |
|
|
|
w = ez . |
|
||
|
|
|
D |
2. Доказать: |
|
||
|
0 1 |
|
2 |
|
Re tg z = |
sin 2x |
; |
|
|
|
cos 2x + ch 2 y |
||||
|
-i |
|
x |
|
Решить уравнение: |
|
|
|
|
|
|
|
|||
|
-2i |
|
|
|
sin z = i . |
|
|
f=?
3.D →{Im w > 0}.
Вариант 8
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : |
|
z |
|
>1, z [− i,− 2i]}, |
w = |
1 |
|
1 |
|
|
|||||||
|
|
|
z + |
; |
||||
|
|
|
|
|
|
2 |
|
z |
|
|
|
|
|
|
2) |
|
< Re z < |
π |
, − |
π |
|
, w = sin z ; |
D = z :0 |
2 |
2 |
< Im z < 0 |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
74 |
|
3) |
D ={z :z [− ∞;+1]}, |
w = z , |
||||||
4) D ={z : |
|
z −1 |
|
< 2, Im z < 0}, w = |
||||
|
|
|||||||
5) |
D = {z : z [0, + ∞)}, |
w = Ln z ; |
||||||
|
w = |
5πi |
. |
|
||||
|
|
|
||||||
|
0 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|||
w(4)= 2 ;
z +1 ; z − 3
z0 = −1−2
2. Решить уравнение: sin z + cos z = 2 . Доказать:
3i , |
w =10πi |
, |
z |
0 |
= i , |
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
Arch z = Ln(z +  z2 −1).
z2 −1).
f=?
3.D ={z : z −1 >1, z +1 >1, Im z > 0} → G ={w : w >1, Re w > 0}.
Вариант 9
1. Найти образы указанных областей D при данных отображениях:
1) |
|
|
|
z |
|
=1,− |
π |
|
; w = |
1 |
|
1 |
|
|
|||||||||||
D = z :Im z < 0, z |
|
|
|
< arg z < 0 |
|
z + |
; |
|||||
|
|
|
|
|
|
|
3 |
|
|
2 |
|
z |
2) D ={z : |
|
z +1 + i |
|
<1, |
|
z |
|
>1}; w |
= |
2z + 3 |
; |
|||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z + i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) D ={z :Im z < 0}; w = z , w(−1)= −i, (ϕ0 = 0); |
||||||||||||||||||||||||
4) |
|
1 |
< |
|
z |
|
< 2,0 < arg z < |
π |
|
w = z2 +1; |
||||||||||||||
|
|
|
||||||||||||||||||||||
D = z : |
|
|
|
; |
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5) |
|
|
π |
< Re z < |
π |
|
|
|
|
|
|
w = sin z . |
||||||||||||
D = z : |
4 |
2 |
, Im z > 0 ; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. Доказать: arctg z = −i arth iz . Вычислить: Arcsin i, Ln(−1). |
||||||||||||||||||||||||
3. D ={z : |
|
z |
|
> |
1, Im z > |
|
|
|
|
|
f =? |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
0} → G ={w :Im w > 0}. |
||||||||||||||||||||||
Вариант 10
1. Найти образы указанных областей D при данных отображениях:
1) D ={z :Im z > 0, (Im z)2 > 4Re z + 4 }; w = z, w(−1)= i ; |
|||||||||||
2) D ={z : |
|
z +1 + i |
|
<1, |
|
z |
|
<1}; w = |
z −1 |
|
; |
|
|
|
|
||||||||
|
|
|
|
z +1 |
|||||||
|
|
|
|
|
|
|
|
|
|
||
3) D ={z : |
|
|
|
|
>1, z [1; + ∞), Re z > 0 }; |
|
|
1 |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
z |
|
|
w = |
|
z + |
|
|
; |
||||||||
|
|
|
2 |
|
z |
||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
< Re z < |
; |
w = sin z |
; |
|
|
|
|
||||||||||
4) D = z :0 |
4 |
, − 2 < Im z < 0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3πi |
|
||||||
5) D ={z : |
|
z |
|
<1, Im z > 0 }; w = Lnz, w(i − i 0)= − |
|
. |
|||||||||||
|
|
||||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2. Вычислить: (1 − i)1+i , |
|
|
|
|
|
|
|
|
|
||||||||
Ln e . Доказать: arch z = i arccos z . |
|||||||||||||||||
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|

3. Найти дробно-линейное отображение такое, чтобы точки (−1, 0,1) переходили в точки (−1, i,1) и образом нижней полуплоскости была внутренность единичного круга с центром в начале координат.
Вариант 11
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : |
|
|
z − i |
|
> 2, Im z < 0}, w |
1 |
|
; |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
z |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
D ={z : − 2 < Im z < −1}, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2) |
|
w = z2 ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3) |
D ={z : |
|
|
z |
|
|
|
|
> 2, z [2,+ ∞)}, |
|
w = |
1 |
|
|
|
1 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
z + |
z |
; |
|
|
|||||||||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
π |
, |
|
|
w = 3 |
z ; |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
D = z :Arg ≠ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) |
|
|
−1 < Re z < |
0, |
π |
< Im z < |
π |
, w = ez . |
|
||||||||||||||||||||||||||||
D = z : |
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
2. Вычислить: ii ; Ln1; Arcctg 2i . Решить уравнение: Ln(z + i)=1. |
|||||||||||||||||||||||||||||||||||||
3. D ={z : |
|
|
|
|
|
|
|
< 2} |
f |
=? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z − i |
|
→ G ={w : Re w > 2}, w(−i)= 2, w(0)= 3. |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 12 |
|
|
|
|
||||||||
1. Найти образы указанных областей D при данных отображениях: |
|||||||||||||||||||||||||||||||||||||
1) D ={z : Im z = 2Re z}, w = |
z − 3 |
|
; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
z + 3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
||||||||
2) |
|
|
< arg z < |
|
|
|
|
|
|
|
, |
|
|
|
w = |
|
|
||||||||||||||||||||
D = z : |
3 |
3 |
π, z [0; i] |
|
|
|
|
z + |
; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
z |
||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
, |
|
w |
= cos z ; |
|||||||||
D = z : 0 < Re z < π, 0 < Im z < |
2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) |
D = {z : (Im z)2 > 2Re z +1}, |
|
w = z , |
|
w(−1)= −i ; |
||||||||||||||||||||||||||||||||
5) |
|
|
|
z |
|
<1, |
π |
< arg z < |
3 |
|
|
, |
|
|
|
w = |
1 |
|
|
+ |
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
D = z : |
|
|
|
8 |
8 |
π |
|
|
|
2 |
z |
z |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Вычислить: Arcth(1 + 2i), Ln |
1(1 + i) . Решить уравнение: ln(i − z)= 0 . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
f=?
3.D ={z : Im z < 0} → G ={w : w − i <1}.
Вариант 13
1. Найти образы указанных областей D при данных отображениях:
76

1)D
2)D
3)D
4)D
={z :1 < Im z < 4 |
}; w = |
1 |
|
+1; |
|
|
||
z |
|
|
||||||
|
|
|
|
|
|
|||
={z :Im z < 0 }; |
|
1 |
|
|
1 |
|||
w = |
|
|
z + |
|
; |
|||
2 |
|
|||||||
|
|
|
|
z |
||||
={z : Im z < π, Re z > 0 }; w = sh z ;
={z :Im z < 0 }; w =  z,
z,  −1 = i (ϕ0 = 0);
−1 = i (ϕ0 = 0);
5) |
|
< Im z < |
π |
|
; |
w = e2z . |
D = z :0 |
2 |
, Re z > 0 |
||||
|
|
|
|
|
|
2.Решить уравнение: cos z = i . Доказать: arctg z = −i arctgiz .
3.D ={z : z >1, z [− 2; −1] [1; 2]} f =?→ G ={w : w <1}.
Вариант 14
1. Найти образы указанных областей D при данных отображениях: |
||||||||||||||||
1) D ={z :1 < Re z < 3}; w = (1 + i)z +1; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
|
π |
|
1 |
|
1 |
|||
|
|
|
|
|
|
|
||||||||||
2) |
D = z : |
|
z |
|
<1, − |
|
π < arg z < − |
|
; |
w = |
|
z |
+ |
|
; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
8 |
|
|
2 |
|
|
2 |
|
z |
||
3) D ={z :Re z < 0, 0 < Im z < π}; w = ez ; |
|
|
|
|
|
|||||||||||
4) |
D ={z : z [1; + ∞)}; |
w = 3 z −1, 3 −1 = −1; |
|
|
|
|||||||||||
5) |
|
< |
π |
w = ctg z . |
|
|
|
|
|
|
||||||
D = z :0 < Re z |
; |
|
|
|
|
|
|
|||||||||
|
|
|
4 |
|
|
|
|
|
|
|
Ln(e). |
|||||
2. Доказать: arcctg z = −i arth iz . Вычислить: Arthi, |
||||||||||||||||
3.D = z :0 < Im z < π f =?→ G ={w : w (− ∞; −1] [1; + ∞)}.
2
Вариант 15
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : |
|
|
|
z |
|
|
<1, Re z > 0}; w = |
|
1 − z |
; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
z + 2 |
|
|
|
1 |
|
1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2) |
D = z :Im z < 0, z |
|
|
z |
|
=1, |
− |
|
|
|
< arg z < |
0 |
; |
w = |
|
z + |
|
; |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
z |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3) |
|
< Re z < |
3, 0 < Im z < |
|
π |
w = ez ; |
|
|
|
|
|
|
|||||||||||||||||
D = z :1 |
|
2 |
; |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
π |
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
4) |
|
z |
|
|
<1; |
< arg z < |
; |
w = z 3 ; |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
D = z : |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
77 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

5) D = |
z : |
x2 |
+ |
y2 |
<1, |
x2 |
+ |
y2 |
|
>1 , a > b >1; |
|
|
|
|
|
|
|||||||
|
|
a2 |
|
a2 −1 |
|
b2 |
|
b2 −1 |
|
||
|
|
|
|
|
|
||||||
при b < z < a, |
w = z + z2 −1 . |
|
|||||||||
2.Вычислить: (−1)ie ; Arctg1. Решить уравнение: ln z +1 =1.
i
3.D ={z :0 < Re z < a, a > 0} f =?→ G ={w :Im w > 0}.
|
|
|
|
|
|
Вариант 16 |
|
|
||||||
1. Найти образы указанных областей D при данных отображениях: |
||||||||||||||
1) D ={z :0 < Im z <1}, |
w = |
|
z |
; |
|
|
|
|
||||||
|
z −i |
|
|
|
πi ; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) |
D ={z : z (− ∞;0] (1; + ∞]}, |
w = ln z, w(i)= |
||||||||||||
|
|
π |
|
π |
|
π |
|
|
|
π |
|
2 |
||
3) |
< Re z < |
, − |
< Im z < |
, w = sin z ; |
||||||||||
D = z :− |
3 |
3 |
4 |
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
4) |
D ={z :1 < |
|
z |
|
< e, 0 < arg z < e }, |
w = ln z +1; |
|
|
1 |
|
1 |
||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
π |
|
3π |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||
5) |
D = z :Im z > 0, z |
|
z |
=1, 0 < arg z < |
|
, |
|
< arg z < π |
, |
w = |
|
z + |
|
. |
|||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
4 |
|
4 |
|
|
|
2 |
|
z |
|||||
|
|
|
|
|
|
|
|||||||||||||
2.Вычислить: Arcsin i, ei . Решить уравнение: ch z = i .
3.D ={z :Im z > 0} f =?→ G ={w : w <1},
w(i)= 0, |
|
|
|
′ |
|
|
|
π |
, |
w(2i)= 0, |
|
′ |
|
|
|
||||||||
arg w (i)= − 2 |
arg w (2i)= 0 . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 17 |
|
|
|
||||
1. Найти образы указанных областей D при данных отображениях: |
|||||||||||||||||||||||
1) D ={z :1 < Im z < 2}, w = |
iz + 2 |
; |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z −1 |
|
|
|
|
|
|||
2) D ={z : − ∞ < Re z < 0, 0 < Im z < π}, w = ez ; |
|
||||||||||||||||||||||
3) |
D ={z : z [1; + ∞)}, |
|
w = 3 z −1 , |
3 −1 = −1; |
|
||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
π |
|
|
w = ctg z ; |
|
|
|
|
|||||||
D = z :0 < Re z < |
4 |
, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) |
|
|
z |
|
< |
3 |
, − |
3 |
π < arg z < − |
π |
w = |
1 |
|
1 |
|||||||||
|
|
||||||||||||||||||||||
D = z : |
|
|
|
|
|
|
, |
|
z + |
. |
|||||||||||||
|
|
|
|
|
|
4 |
|
8 |
|
|
|
|
|
|
|
8 |
|
|
2 |
|
z |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. Доказать: Arcctg z = |
i |
|
|
Ln |
z − i |
. Решить уравнение: cos2 z −1 = 0 . |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
z + i |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
f =? |
G ={w : |
|
|
|
|
|
′ |
|||
|
|
|
|
|
|
|
|
|
||||||||||||
3. D = z : |
|
arg z |
|
< |
|
|
→ |
w |
|
|
|
|
||||||||
|
|
4 |
<1, w(1)= 0, arg w |
(1)= π}. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 18 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Найти образы указанных областей D при данных отображениях: |
||||||||||||||||||||
1) D ={z : |
|
z −1 |
|
< 2}, |
w = |
2iz |
; |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z + 3 |
|
|
|
|
|
||
2) D ={z : 0 < Im z <1}, |
|
|
|
|
|
|||||||||||||||
w = z2 ; |
|
|
|
|
|
|||||||||||||||
3) D ={z : |
|
z |
|
>1, z [− 2;−1]U[1;+ ∞)}, |
w = |
1 |
|
1 |
|
|||||||||||
|
|
|||||||||||||||||||
|
|
2 |
z + |
z |
; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
D = |
z : |
x2 |
− |
y2 |
>1 |
, |
w = z + z2 −1 , w(+ ∞)= 0 ( 0 < α < π ); |
|
|
|||||||
|
|
|
cos2 α |
|
sin2 α |
|
|
2 |
|
|
|
|
|
|
5) D ={z : 0 < Re z < a, a > 0, b < Im z < 0, b < 2π,b < 0 }, w = ez .
2.Доказать: Imch z = sh xsin y .
Найти все значения функций: arcsin10 ; Ln (1); 1− 3 .
3 .
f=?
3.D ={z : z <1, Im z > 0, Re z > 0} → G ={w : Im w < 0}.
Вариант 19
1. Найти образы указанных областей D при данных отображениях:
1) |
D ={z :z [1,+∞) }, |
w = 3 z −1 , |
|
3 −1 = −1; |
||||||
2) |
|
|
|
π |
|
|
|
|||
D = z :0 < Re z < |
4 |
, w = ctg z ; |
|
|
||||||
|
|
|
|
|
|
|
|
|||
3) |
D ={z :Re z < 0, 0 < Im z < π}, |
w = ez ; |
|
|||||||
4) |
D ={z :1 < |
|
z |
|
< e, 0 < arg z < e }, |
w = ln z +1; |
||||
|
|
|||||||||
5) |
D ={z : Im z < 0, Re z < 0}, w = |
1 |
|
1 |
||||||
2 |
z + |
. |
||||||||
|
|
|
|
|
|
|
|
|
z |
|
2. Вычислить: 1πi , Ln(2i), cos(2 + i). Решить уравнение sin z = πi .
3. |
|
|
z |
|
|
1 |
|
f =? |
|
|
|||||||
D = |
|
|
<1, z [−1;0]U |
|
,1 |
→ G ={Im < 0}. |
||
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
Вариант 20
1. Найти образы указанных областей D при данных отображениях:
1) D ={z : |
|
z |
|
> 2, Re z < 0, Im z > 0 }, |
w = |
1 |
|
1 |
|
|
|||||||
|
|
|
z + |
; |
||||
|
|
|
|
|
|
2 |
|
z |
79 |
|
|||||||
|
|
|
|
|||||
2) |
|
π |
, |
w = cos z ; |
|
|
|
|
||||||||
D = z : 0 < Re z < |
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
z + 2 |
|
|
||||||||
3) D ={z : |
|
z |
|
<1, Re z > 0, Im z < 0}, w = |
|
; |
||||||||||
|
|
|||||||||||||||
|
|
|
2z +1 |
|||||||||||||
4) D ={z : |
|
|
|
|
|
< 9, Re z < 0}, |
|
|
|
|||||||
|
z |
|
w = z , |
−1 = i ( ϕ0 = 0 ); |
||||||||||||
|
|
|||||||||||||||
5) |
D ={z : 0 < Im z < π}, |
w = cth z . |
|
|
|
|
||||||||||
2. Доказать: arcsin z = −i arsh iz . Решить уравнение: sin z +sin 2z = 0 .
3. D ={z : Im z > 0, z [ia,+i∞), a > 0 } |
f =? |
}. |
→ G ={Im w > 0 |
Вариант 21
1. Найти образы указанных областей D при данных отображениях:
1) |
|
π |
, − |
π |
< Im z |
< |
|
|
|
|||||
D = z : 0 < Re z < |
4 |
4 |
0 , w = sin z ; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||
2) |
D ={z : |
|
z |
|
< 2, 0 < Re z <1}, w |
= |
z +1 |
|
; |
|||||
|
|
|||||||||||||
|
|
z −1 |
||||||||||||
|
D ={z : Im z > 0 }, |
|
|
|
|
|
|
w(0)= −i ; |
||||||
3) |
|
w = z + z2 −1 , |
||||||||||||
4) |
D ={z : 0 < Im z < π, Re z > 0 }, |
w = cth z ; |
||||||||||||
5) |
D ={z : α < Re z <β, γ < Im z < δ}, |
|
δ− γ ≤ 2π, w = ez . |
|||||||||||
2. Доказать: arsh z = −i arcsiniz . Решить уравнение: ln z +i 1 =1
3. D ={z : − π < Re z < π, z [0,π)} |
f =? |
→ G ={Im w > 0}. |
Вариант 22
1. Найти образы указанных областей D при данных отображениях:
1) |
D ={z : z [0,+∞) }, |
w = 3 z , |
w(−1)= −1; |
|||||||||||
2) |
D ={z : z [i,+i∞), z (−i∞,−i]}, |
w = Arsh z ; |
||||||||||||
3) |
|
π |
|
|
|
; |
||||||||
D = z : 0 < Re z < |
, w = tg z |
|||||||||||||
|
|
4 |
|
|
|
|
||||||||
4) |
D ={z : r1 < |
|
z |
|
< r2 , z [r1,r2 ]}, |
w = ln z ; |
||||||||
|
|
|||||||||||||
5) |
D ={1 < |
|
z |
|
< 2 }, |
w = |
z |
|
. |
|
||||
|
|
|
||||||||||||
|
|
z −1 |
80 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
