
- •Часть I. Механика
- •Раздел 1. Введение
- •Раздел 2. Кинематика
- •6. Волновое движение
- •Раздел 3. Законы динамики
- •Раздел 4. Законы сохранения
- •1. Момент импульса считается постоянным в замкнутой систем.
- •2. Если система не замкнута, но существует ось, относительно которой векторная сумма моментов сил равна нулю, то момент импульса системы, относительно этой же оси, остаётся постоянным.
- •Раздел 5. Гравитационное поле
- •Раздел 6. Движение в неинерциальных системах отсчета
- •Раздел 7. Элементы теории относительности. Примеры.
Конспект лекций.
Часть I. Механика
Раздел 1. Введение
Математический аппарат физики. Векторы и операции с ними
Вектор
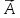 характеризуется модулем (длиной) и
направлением.
Любой
вектор равен своей длине, умноженной
на единичный вектор
характеризуется модулем (длиной) и
направлением.
Любой
вектор равен своей длине, умноженной
на единичный вектор
 своего
направления:
своего
направления: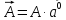
Вектор
суммы векторов
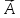 и
и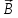 ,
есть
вектор
,
есть
вектор
 ,при
этом он является диагональю параллелограмма,
построенного на векторах
,при
этом он является диагональю параллелограмма,
построенного на векторах
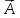 и
и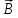 как на сторонах.
как на сторонах.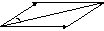
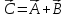
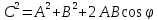
Вектор
разности двух векторов
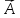 и
и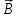 -
есть
вектор
-
есть
вектор
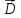 ,соединяющий
концы вычитаемых векторов, приведенных
к одному началу и направленный в сторону
уменьшаемого.
,соединяющий
концы вычитаемых векторов, приведенных
к одному началу и направленный в сторону
уменьшаемого.

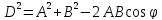
Изменение
вектора как по величине так и по
направлению:
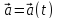
Изменение
за время
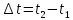 :
: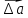 (t)=
(t)=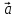 (t2)
-
(t2)
-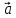 (t1
)Умножение
векторов:
(t1
)Умножение
векторов:
Скалярное произведение:
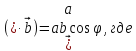 -угол
между векторами.
-угол
между векторами.
Векторное произведение:
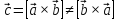
Длина
вектора
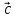 :
: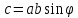 .
.
Направление
вектора
 :
: ,
,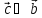 ,
,
если
смотреть с конца вектора
 ,
то направление кратчайшего поворота
от первого вектора ко второму против
часовой стрелки.
,
то направление кратчайшего поворота
от первого вектора ко второму против
часовой стрелки.
Разложение вектора на составляющие:
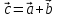
Проекция
вектора на ось
есть число, равное
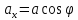
Если взять оси декартовой системы координат, то:
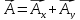 -
составляющие вектора.
-
составляющие вектора.
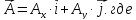 –
–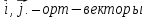
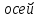 ,
,
 -проекции
вектора на оси.
-проекции
вектора на оси.
Дифференцирование
вектора:
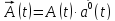
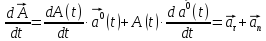
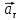 –коллинеарен
исходному, характеризует изменение
–коллинеарен
исходному, характеризует изменение
вектора только по величине (касательная).
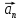 –перпендикулярен
исходному, характеризует изменение
–перпендикулярен
исходному, характеризует изменение
вектора только по направлению (нормаль).
Момент вектора относительно точки и оси:
Момент вектора относительно точки О – это вектор
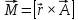 Вектор
Вектор
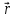 -соединяет
точку О с началом вектора
-соединяет
точку О с началом вектора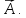
Момент вектора относительно оси, проходящей через точку O – это проекция вектора
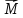 на эту ось.
на эту ось.
Раздел 2. Кинематика
Материальная точка. Система отсчета. Траектория. Перемещение и путь. Скорость и ускорение. Тангенциальное и нормальное ускорения. Классификация движения по ускорению. Кинематика прямолинейного и вращательного движений точки. Кинематика колебательного и волнового движений. Примеры, практические задачи.
Движение твердого тела. Степени свободы. Поступательное и вращательное движение твердого тела. Теорема Эйлера о произвольном движении твёрдого тела.
Механическое движение – это изменение положения (перемещение) тела в пространстве, относительно других тел.
Предварительно введем следующие упрощения:
От реальных тел мы перейдём к материальной точке (тело, размерами которого можно пренебречь в условиях нашей задачи)
Пусть есть точка O – тело отсчета, материальная точка M – тело, которое движется относительно O (тело отсчета неподвижно).
Вектор
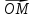 –радиус-вектор
–радиус-вектор
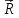 .
Если вектор меняется, то точка движется.
.
Если вектор меняется, то точка движется.
Системы отсчета:
Векторная система отсчета. Переменные величины- радиус вектор, время.
Зависимость радиус-вектора точки от времени – уравнение движения:
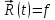 (t)
(t)Скоростью движения материальной точки мы называем первую производную от радиуса-вектора по времени:
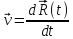
Ускорением материальной точки мы называем первую производную от вектора скорости по времени (вторую производную от радиуса-вектора по времени):
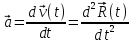
Декартова система отсчета. Тело отсчёта- начало прямоугольной системы координат xyz и время. Положение точки определяется тремя числами-координатами.
Радиус-вектор в декартовой системе:
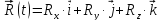 .
Здесь
.
Здесь
 ,
,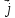 ,
,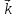 -орт-векторы
соответствующих осей.
-орт-векторы
соответствующих осей.
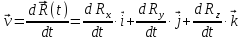 =
=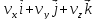
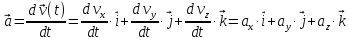
 Цилиндрическая,
полярная система отсчета
Цилиндрическая,
полярная система отсчета
Тело отсчета – полюс. Чтобы задать положение относительно
полюса
нужны 3 числа: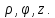
В цилиндрической системе отсчета удобно описывать движение тела
(материальной точки) по окружности. В этом случае
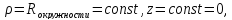 если
точка отсчёта взята в центре окружности,
расположенной в плоскости
если
точка отсчёта взята в центре окружности,
расположенной в плоскости
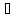 к осиZ
. Тогда положение точки относительно
полюса зависит только от 𝜑
к осиZ
. Тогда положение точки относительно
полюса зависит только от 𝜑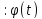 –
определяет уравнение движение точки
по окружности.
–
определяет уравнение движение точки
по окружности.
Координаты в различных системах отсчета связываются между собой следующими соотношениями:
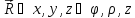
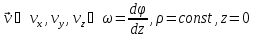
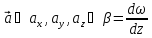
Здесь-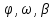 –угловая
координата, угловая скорость, угловое
ускорение соответственно.
–угловая
координата, угловая скорость, угловое
ускорение соответственно.
Для
движения по окружности:
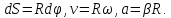
Движения в механике можно свести к 4 типам:
Поступательное движение – это движение, при котором любая прямая, проводимая в теле остается параллельна самой себе.
Вращательное движение. Простейшим примером является вращение тела относительно неподвижной оси: движение, при котором радиусы всех точек тела поворачиваются на равные углы.
Колебательное движение – это движение, при котором положение тела в пространстве повторяется через равные промежутки времени.
Волновое движение – это процесс распространения колебаний в пространстве с течением времени.
Классификация механического движения по ускорению
По
определению:

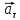 –тангенциальное
ускорение,
характеризует изменение вектора
–тангенциальное
ускорение,
характеризует изменение вектора
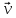 только по величине.
только по величине.
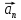 –нормальное
ускорение,
характеризует изменение вектора
–нормальное
ускорение,
характеризует изменение вектора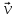 только по направлению.
только по направлению.
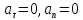 ,
вектор
скорости не изменяется ни по величине
,
вектор
скорости не изменяется ни по величине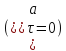 , ни по направлению (
, ни по направлению (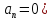 , это –равномерное,
прямолинейное движение.
Найдём параметры и закон движения.
, это –равномерное,
прямолинейное движение.
Найдём параметры и закон движения.
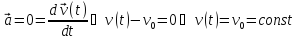
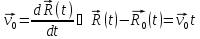
Закон
движения:
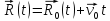 .
–в
векторной системе отсчёта.
.
–в
векторной системе отсчёта.
В
декартовой системе координат:
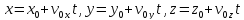
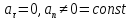 Это
означает, что модуль вектора скорости
не меняется, в то время как за любые
равные промежутки времени
его
направление меняется на равные углы
Это
означает, что модуль вектора скорости
не меняется, в то время как за любые
равные промежутки времени
его
направление меняется на равные углы
Это- равномерное движение по окружности. Найдём параметры и закон движения.
 =
=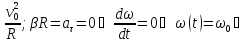
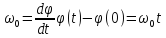 .
.
Закон
движения:
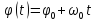
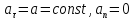 равнопеременное,
прямолинейное движение
(
равнопеременное,
прямолинейное движение
(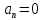 );
);
(равноускоренное
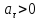 или
равнозамедленное
или
равнозамедленное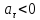 )
)
Так
как вектор скорости не меняется по
направлению (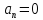 ), то пусть движение происходит по
направлению осиOX.
Найдём параметры и закон движения.
), то пусть движение происходит по
направлению осиOX.
Найдём параметры и закон движения.
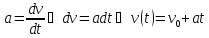 Закон
Закон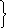
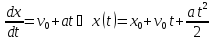 движения
движения
В
общем случае:
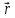 =
=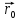 +
+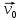 t
+
t
+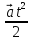 ;
;
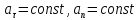 –равнопеременное
(
–равнопеременное
(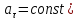 движение по окружности
движение по окружности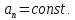
 Угловое
ускорение
Угловое
ускорение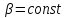 в силу
в силу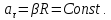 Найдём параметры и закон движения в
угловых переменных.
Найдём параметры и закон движения в
угловых переменных.
 Угловая
скорость и закон
Угловая
скорость и закон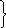
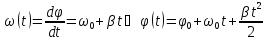 движения
движения
Колебательное, - движение, при котором координаты точки повторяются через равные промежутки времени (периоды). Простейшими периодическими функциями являются гармонические функции времени- синус или косинус. При этом как первая, так и вторая их производные будут также гармоническими функциями. Поэтому легко «угадать» вид ускорения при гармонических колебаниях материальной точки:

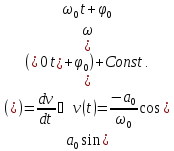
 случая
случая
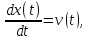 легко найти закон изменения координаты:
легко найти закон изменения координаты:
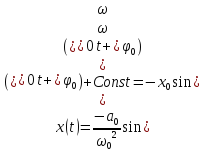 +
Const.
+
Const.
Постоянные
интегрирования, начальная фаза
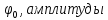
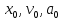 ,
находятся из начальных условий при
решении динамических дифференциальных
уравнений колебаний. Циклическая частота
,
находятся из начальных условий при
решении динамических дифференциальных
уравнений колебаний. Циклическая частота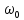 (число
полных колебаний за 2
(число
полных колебаний за 2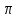 секунд) зависит от колебательных свойств
системы.
секунд) зависит от колебательных свойств
системы.
Итак,
закон гармонического колебания:
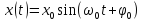 .Учитывая,
что
.Учитывая,
что
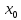 =
=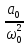
получим:
 x(t).
Ускорение точки пропорционально
смещению от положения равновесия и
направлено в сторону точки равновесия.
x(t).
Ускорение точки пропорционально
смещению от положения равновесия и
направлено в сторону точки равновесия.
