РАБОТА №146

ИЗМЕРЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ

Цель работы. Измерение коэффициента внутреннего трения (вязкости) жидкости методом Стокса.

Приборы и принадлежности. Вискозиметр с жидкостью; твердые шарики; мерная линейка; секундомер.

Введение

Вязкостью или внутренним трением называется свой­ство всех веществ оказывать сопротивление их течению-перемещению одного слоя вещества относительно другого.

Внутреннее трение представляет собой одно из яв­лений переноса и определяется тепловым движением, раз­мерами и формой молекул, действием молекулярных сил.

Для объяснения возникновения сил вязкости рас­смотрим две параллельные пластинки, разделенные слоем жидкости (рис. 1).

Рис. 1

Пусть нижняя пластинка удерживается неподвижно, а верхняя движется параллельно нижней в направлении х. Мысленно разделим весь слой жидкости на ряд тонких па­раллельных слоев. Молекулы слоя, прилегающие к верхней пластинке, «прилипают» к ней и перемещаются вместе с ней с той же скоростью. Этот слой жидкости увлекает за собой следующий слой, который перемещается с меньшей скоростью и т.д.

Слой жидкости, прилегающий к нижней неподвиж­ной пластинке, остаётся в покое. Чем больше удален слой от нижней пластинки, тем быстрее он перемещается. Быст­роту изменения скорости можно охарактеризовать отноше­нием , где - разность скоростей двух слоев жид­кости, расстояние между которыми равно . Предел этой величины равен

(где - градиент скорости. Здесь ось y перпендику­лярна направлению перемещения жидкости).

Вязкость жидкости проявляется в её сопротивлении относительному сдвигу соприкасающихся слоев, а, следо­вательно, и пластинок. Возникающая при этом сила сопро­тивления называется силой внутреннего трения.

И. Ньютон в 1687 году сформулировал закон, согла­сно которому при ламинарном (безвихревом) течении жид­кости сила внутреннего трения пропорциональна градиен­ту скорости:

(где S - площадь поверхности соприкосновения двух слоев, смещающихся друг относительно друга; - коэффициент вязкости или коэффициент внутреннего трения жидкости).

При больших скоростях ламинарное течение жид­кости переходит в турбулентное (вихревое) и закон нару­шается.

В системе СИ единицей вязкости является 1 Па·с. Это величина, при которой 1 м² слоя жидкости испытывает действие силы в 1 Н при градиенте скорости 1 с^-1 .

Вязкость газа обусловлена тепловым движением молекул, она увеличивается с повышением температуры. В отличие от газов, молекулы жидкости большую часть времени находятся вблизи положения равновесия, и поэтому движущийся слой жидкости увлекает соседние слои в основном за счёт моле­кулярных сил сцепления. Вязкость жидкости убывает с по­вышением температуры. Так при повышении температуры воды от 0°С до 100°С её вязкость уменьшается с 1,8·10^-3 до 2,8·10^-4 Па·с. Особенно сильно она меняется у масел; например, у касторового масла при перепаде температуры с 18⁰С до 40⁰С вязкость уменьшается в четыре раза.

Отмеченные выше свойства жидкости, рассмотрен­ные для случая плоскопараллельных её слоев, остаются справедливы и при движении других тел в жидкости, од­нако, при этом следует учитывать ещё возможность вли­яния таких факторов как форма и размеры тела, характер обтекания их жидкостью и т. д.

Описание установки и методика измерения

П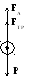риборы, служащие для измерения вязкости, назы­ваются вискозиметрами. В данной работе применяется вис­козиметр, основанный на использовании метода Стокса, в основе которого лежат процессы, определяющие характер свободного движения твёрдого шарика, опущенного в жид­кость. В этом случае на шарик действуют три силы (рис. 2).

Рис. 2

1. сила тяжести Р, направленная вертикально вниз и равная

(1)

(где r – радиус шарика, - плотность материала шарика при данной температуре; g – ускорение свободного падения).

2. сила Архимеда F_A, направленная вертикально вверх и равная весу жидкости, вытесненной шариком,

(2)

(где - плотность жидкости при данной температуре).

3. сила внутреннего трения F_тр направлена в сторону, обратную скорости движения (в нашем случае вертикально вверх); ее можно рассчитать по формуле Стокса:

(3)

(где V – скорость равномерного движения шарика; - коэффициент внутреннего трения).

Силы P и F_A постоянны, а F_тр растет с увеличением скорости шарика. Это происходит до тех пор, пока равнодействующая всех сил не станет равной нулю:

. (4)

Начиная с этого момента шарик движется равномерно.

Подставляя (1), (2) и (3) в уравнение (4), получим условие равномерного движения шарика в виде:

Заменив в полученном соотношении радиус шарика на его диаметр , а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени , получаем окончательное выражение для расчета коэффициента вязкости жидкости:

(5)

Уравнение (5) справедливо для случая, когда шарик падает в безграничной среде. Если шарик движется вдоль оси трубки, то необходимо учитывать влияние стенок трубки. Это влияние обусловлено тем, что молекулы слоя жидкости, прилегающие к внутренним стенкам трубки, «прилипают» к ней и не перемещаются.

В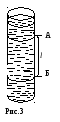искозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.

Наблюдая за характером равномерного движения шарика в жидкости и используя соотношение (5), можно определить коэффициент внутреннего трения жидкости.

Порядок работы

и обработки результатов измерений

1. Отобрать для опыта пять шариков;

2. Измерить диаметр каждого шарика три раза в различных направлениях и данные измерений занести в табл. 1;

3. Измерить расстояние между метками на вискозиметре с точностью до 1 мм;

Таблица 1

Номер шарика	Диаметр шарика d, см.			Средний диаметр шарика dср, см
	1	2	3
1
2
3
4
5

4. Опустить шарик в вискозиметр через воронку и измерить время его движения между метками;

Измерение повторить для каждого из пяти шариков. Данные опыта занести в таблицу 2.

Таблица 2

Номер шарика	dср, см	l, см.	t, с.	, Па·с
1
2
3
4
5
			ср=

4. Вычислить коэффициент внутреннего трения по результатам каждого опыта. Определить среднее значение этого коэффициента.

П р и м е ч а н и е. При проведении опытов фиксируются: наименование жидкости, ее плотность, температура окружающей среды и плотность материала шарика.

Оценить абсолютную погрешность измерения коэффициентов вязкости по методу Стьюдента.

Для этого необходимо найти

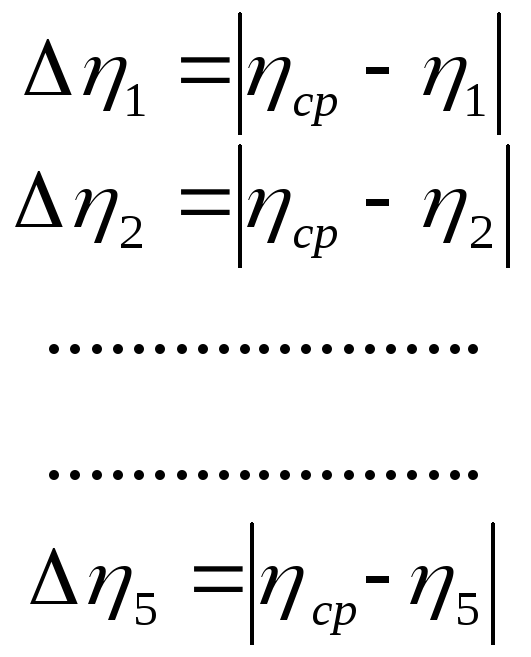
и вычислить вспомогательную величину

где n – число измерений коэффициента вязкости.

Затем вычислить абсолютную погрешность по формуле

где а – коэффициент Стьюдента, равный 2.8 для доверительной вероятности =0.95 при n=5.

Окончательный результат записать в виде

Контрольные вопросы.

1. В чем заключается физическая природа вязкости?

2. При каких условиях сила внутреннего трения пропорциональна скорости?

3. Объясните характер зависимости коэффициента внутреннего трения от температуры?

4. Напишите размерность коэффициента трения.

5. Каков характер изменения скорости и ускорения шарика на всем пути его движения?

6. Как изменяется скорость падения парашютиста при затяжном прыжке?

Литература

1. Савельев И.В. Курс общей физики, т.2..М.: Наука, 1987

2. Матвеев А.Н. Молекулярная физика. М.: Высшая школа, 1981

3. Кикоин А.К. Молекулярная физика. М.: Наука, 1982

Содержание

Цель работы………………………………………………..	3
Введение……………………………………………………	3
Описание установки и методика измерения……………..	5
Порядок выполнения работы и результаты измерений…	8
Контрольные вопросы…………………………………….	10
Литература…………………………………………………	10

10