
- •2. Досліди Майкельсона-Морлі
- •3. Перетворення Лоренца
- •4. Постулати ств
- •5. Елементи релятивістському динаміки
- •6. Відносність проміжків часу
- •А) Лабораторна робота № 1
- •Методика виконання роботи
- •Завдання до роботи
- •Порядок виконання роботи
- •Обробка результатів
- •5. Висновки з роботи
- •6. Питання до самоперевірки
- •7. Відносність відстаней
- •Б) Лабораторна робота № 2
- •Методика виконання роботи
- •Завдання до роботи
- •Порядок виконання роботи
- •Обробка результатів
- •5. Висновки з роботи
- •6. Питання до самоперевірки
Обробка результатів
Занести отримані в попередньому пункті результати до таблиці 1.
|
П/п |
Y, м/с |
|
β |
l, м |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
5. Висновки з роботи
6. Питання до самоперевірки
1.Перетворення Лоренца.
2. Дослідження Майкельсона- Морли.
3. У чому полягає відносність відстаней ?
4.У чому полягає спеціальна теорія відносності Ейнштейна?
5. Запишіть вираз відносності відстаней.
6. У чому полягає відносність часу?
7. Запишіть вираз відносності часу.
8. Сформулюйте постулати Ейнштейна.
7. Відносність відстаней
Нехай
твердий стержень покоїться в системі
відліку K
', що рухається зі швидкістю υ
щодо системи відліку K
(рис. 4.1). Стержень
орієнтований паралельно осі x '. Його
довжина, виміряна за допомогою еталонної
лінійки в системі K ', дорівнює
l0. Її
називають власною
довжиною. Якою
буде довжина цього стержня, виміряна
спостерігачем в системі K? Для
відповіді на це питання необхідно дати
визначення процедури вимірювання
довжини рухомого стержня.
Під
довжиною стержня в системі K, щодо якої
стержень рухається, розуміють відстань
між координатами кінців стержня,
зафіксованими одночасно по годинах
цієї системи. Якщо
відома швидкість системи K 'щодо K, то
вимірювання довжини рухомого стержня
можна звести до вимірювання часу: довжина
l рухається зі швидкістю υ стержня
дорівнює добутку υτ0, де τ0 - інтервал
часу щогодини в системі K між проходженням
початку стержня і його кінця повз
який -небудь
нерухомої точки (наприклад, точки A) в
системі K (рис. 4.1). Оскільки
в системі K обидві події (проходження
початку і кінця стержня повз фіксованої
точки A) відбуваються в одній точці, то
проміжок часу τ0 в системі K є власним
часом. Отже,
довжина l рухомого стержня дорівнює
l = υτ0.
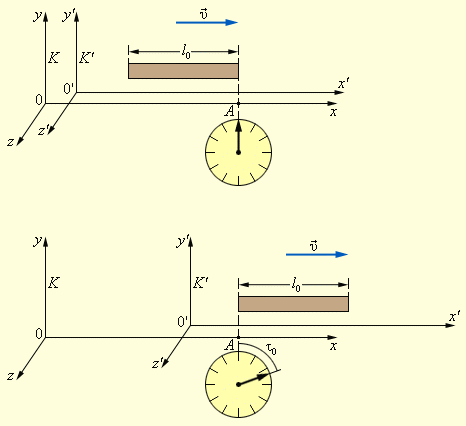 Рис.
4.1.
Вимірювання
довжини рухомого стержня
Знайдемо
тепер зв'язок між l і
l0. З
точки зору спостерігача в системі K ',
точка A, що належить системі K, рухається
уздовж нерухомого стержня наліво зі
швидкістю υ, тому можна записати
l0 = υτ,
де
τ є проміжок часу між моментами проходження
точки A повз решт стержня, виміряний по
синхронизованной годинах у K
'. Використовуючи
зв'язок між проміжками часу τ і τ0
Рис.
4.1.
Вимірювання
довжини рухомого стержня
Знайдемо
тепер зв'язок між l і
l0. З
точки зору спостерігача в системі K ',
точка A, що належить системі K, рухається
уздовж нерухомого стержня наліво зі
швидкістю υ, тому можна записати
l0 = υτ,
де
τ є проміжок часу між моментами проходження
точки A повз решт стержня, виміряний по
синхронизованной годинах у K
'. Використовуючи
зв'язок між проміжками часу τ і τ0![]() ,
знайдемо
,
знайдемо
![]() Таким
чином, довжина стержня залежить від
системи відліку, в якій вона вимірюється,
тобто є відносною величиною. Довжина
стержня виявляється найбільшою в тій
системі відліку, в якій стержень
спочиває. Рухомі
щодо спостерігача тіла скорочуються в
напрямку свого руху. Цей
релятивістський ефект носить назву
лоренцева
скорочення довжини.
Таким
чином, довжина стержня залежить від
системи відліку, в якій вона вимірюється,
тобто є відносною величиною. Довжина
стержня виявляється найбільшою в тій
системі відліку, в якій стержень
спочиває. Рухомі
щодо спостерігача тіла скорочуються в
напрямку свого руху. Цей
релятивістський ефект носить назву
лоренцева
скорочення довжини.
Відстань не є абсолютною величиною, воно залежить від швидкості руху тіла відносно даної системи відліку. Скорочення довжини не пов'язано з якими-небудь процесами, що відбуваються в самих тілах. Лоренцева скорочення характеризує зміну розміру рухомого тіла в напрямку його руху. Якщо стержень на рис. 4.4.1 розташувати перпендикулярно осі x, вздовж якої рухається система K ', то довжина стержня виявляється однаковою для спостерігачів в обох системах K і K'. Це твердження знаходиться у відповідності з постулатом про рівноправність усіх інерційних систем. Для доказу можна розглянути наступний уявний експеримент. Розташуємо в системах K і K 'уздовж осей y і y' два жорстких стержня. Стрижні мають однакові власні довжини l, виміряні нерухомими по відношенню до кожного зі стрижнів спостерігачами в K і K ', і один з кінців кожного стержня збігається з початком координат O або O'. У деякий момент стрижні виявляються поруч і представляється можливість порівняти їх безпосередньо: кінець кожного стержня може зробити позначку на іншому стрижні. Якщо б ці позначки не співпали з кінцями стрижнів, то один з них виявився б довше іншого з точки зору обох систем відліку. Це суперечило б принципу відносності.
Незмінність довжини рухомого стержня, орієнтованого перпендикулярно до напрямку руху, була використана в § 4.3 при аналізі релятивістського уповільнення часу.
Слід звернути увагу, що при малих швидкостях руху (υ <<c) формули СТВ переходять в класичні співвідношення: l ≈ l0 и τ ≈ τ0. Таким чином, класичні уявлення, що лежать в основі механіки Ньютона і сформовані на основі багатовікового досвіду спостереження над повільними рухами, в спеціальній теорії відносності відповідають граничному переходу при β = υ / c → 0. У цьому виявляється принцип відповідності.

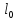 .,
м
.,
м ,
с
,
с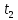 ,
с
,
с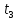 ,
с
,
с