УДК 683.1

Методические указания содержат сведения необходимые для выполнения цикла лабораторных работ по исследованию непрерывных и дискретных систем автоматического управления (САУ) с применением многофункциональной интегрированной системы автоматизации математических и научно-технических расчетов MATLAB, пакета моделирования динамических систем Symulink и программы моделирования

VisSim.

Методические указания, подготовленные на кафедре «Вычислительная техника», предназначены для студентов специальности 22.01.00, изучающих курсы «Моделирование» и «Основы теории управления».

Составители: П.П. Макарычев, А.С. Бычков

2

Введение

Лабораторные работы, приведенные в данном методическом пособии, предназначены для студентов электротехнических специальностей, изучающих курсы: «Основы теории управления», «Моделирование систем управления» и им подобных. Лабораторные исследования проводятся на персональных ЭВМ с применением моделирующих пакетов MATLAB, VisSim и Electronics Workbench. При разработке лабораторного практикума преследовалась цель заменить процесс решения дифференциальных уравнений движения моделированием и уделить максимум внимания постановке задач теории управления и интерпретации результатов. Вся совокупность учебных моделей разбита на две группы. Ядром являются модели, для пакета VisSim, которые не отражают особенности конкретных систем, поскольку являются чисто математическими, т.е. построены на основе задания структурных схем и передаточных функций. Эта совокупность моделей может быть использована для любой специальности вплоть до нетехнических. Вторая группа моделей для пакета Electronics Workbench разработана для студентов электротехнических специальностей и отражает особенности технической реализации систем управления на основе электронных устройств. Совокупность работ рассчитана на выполнение в течение одного семестра.

3

Лабораторная работа № 1

ПОСТРОЕНИЕ ГРАФИКОВ КОМПЛЕКСНЫХ НЕПРЕРЫВНЫХ ФУНКЦИЙ

1. Основные сведения Комплексное число может быть представлено в трех видах:

a+jb=Acosα+jAsinα=Aejα,

т.е. в алгебраической форме, в тригонометрической и в показательной. Число A называется модулем или абсолютной величиной комплексного

числа. Модуль однозначно определяется соотношением:

A=√a2+b2.

Угол α называется аргументом, α=arctg(b/a).

Каждому комплексному числу соответствует одна определенная точка на числовой или комплексной плоскости. Каждой точке числовой плоскости соответствует только одно комплексное число.

Положим, что из начала координат в числовой плоскости проведен ряд векторов. Каждый такой вектор вполне определяет точка комплексной плоскости, которая находится в его конце, а в таком случае каждому вектору будет соответствовать лишь одно комплексное число. Поэтому векторы, проведенные из начала координат, можно символически изображать комплексными числами, соответствующими точкам, в которых располагаются их концы.

Оси 0x и 0y (в прямоугольной декартовой системе координат) называются соответственно действительной и мнимой осью. Абсцисса и ордината каждой точки на плоскости изображают соответственно действительную часть a и мнимую часть b комплексного числа.

Если аргумент комплексного числа Aejα меняется во времени, т.е. α=ωt, то точка, соответствующая этому комплексному числу, перемещается со временем в числовой плоскости против направления вращения часовой стрелки с угловой скоростью ω, описывая окружность с радиусом A и с

4

центром в начале координат. Следовательно, комплексное число Aejωt соответствует вращающемуся вектору и может быть им изображено.

Комплексную функцию от действительной переменной x можно представить в виде:

W(jx)=U(x)+jV(x)=A(x)ejϕ(x),

где A(x)= √U(x)2+V(x)2 ,

ϕ(x)=arctgV(x)/U(x)

На комплексной плоскости функция W(x) определяет вектор, длина (модуль) которого равна A(x), а аргумент (угол, образованный этим вектором с положительной действительной полуосью) — ϕ(x). Кривую, которую описывает конец этого вектора при изменении аргумента от нуля до бесконечности, годографом функции.

Действительную и мнимую часть функции W(x) будем называть соответственно вещественной и мнимой функцией.

Модуль функции называют амплитудной функцией, ее график— амплитудной характеристикой. Аргумент называют фазовой функцией, а ее график — фазовой характеристикой.

Амплитудная характеристика показывает изменение отношения амплитуд, а фазовая — сдвиг фазы выходной величины относительно входной в зависимости от изменения входного воздействия.

2.Лабораторное задание

2.1.По согласованию с преподавателем выберете из банка заданий комплексные функции f1(x), g1(x), h1(x).

2.2.Постройте графики модуля и аргумента непрерывной комплексной функции f1(x).

2.3.Постройте графики вещественной и мнимой части непрерывной комплексной функции g1(x).

5

2.4.Постройте годограф для непрерывной комплексной функции h1(x).

6

Лабораторная работа № 2 ПОСТРОЕНИЕ ГРАФИКОВ КОМПЛЕКСНЫХ РЕШЕТЧАТЫХ

ФУНКЦИЙ

1.Основные сведения

Вдискретных системах управления входные и выходные сигналы представляют собой временные ряды, т.е. упорядоченные последовательности отсчетов. Для любой упорядоченной последовательности

[xk ]=[... x−1 , x0 , x1 , x2 , x3 , ...] z – преобразование определяется следующим образом

∞

X ( z ) = ∑xk z−k ,

k =−∞

где z – непрерывная комплексная переменная; X ( z ) – двустороннее z –

преобразование. Одностороннее z – преобразование имеет место, если для всех отрицательных k значения xk = 0 [ ].

Для последовательности отсчетов [xk ] экспоненциальной функции,

приведенной на рис. 1,

z – преобразование есть простая рациональная функция от a и z , т.е.

Это преобразование равно нулю в точке z =0 и становиться бесконечным в точке z =exp( −a ).

7

Следовательно, бесконечную или конечную сумму отсчетов всегда можно записать в виде рациональной функции. При этом, в z – преобразовании содержится вся информация об исходной последовательности отсчетов. По z – преобразованию можно полностью восстановить все множество отсчетов. Другими словами, всегда существует обратное z – преобразование.

Передаточная функция дискретной линейной системы равна отношению z – преобразования выходного сигнала к z – преобразованию входного сигнала X ( z ) и имеет вид

Простая замена z на exp( j( 2π − ω)) , где ω – циклическая частота, позволяет

действительными числами, то имеем W( j( 2π − w )) =W ( − jw )). Передаточная

называется центральной частотой, частота ω= 2π – частотой отсчетов. Для дискретной передаточной функции

W ( z ) = 0,27( z2 +1)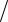( z2 −1,27z + 0,81)

частотный отклик имеет вид

Амплитуда и фаза частотного отклика W( jω) называется коэффициентом

8

передачи по амплитуде и фазовым сдвигом дискретной линейной системы. Из (1) имеем следующее соотношение

W( jω) = Re( jω) + Im( jω).

Следовательно, коэффициент передачи по амплитуде

K( jω) = W( jω) =[Re2( jω) + Im2( jω)]12 ,

а фазовый сдвиг

ϕ( jω) = arg(W ( jω)) =tg −1( I( jω)Re( jω)) .

Графики зависимости коэффициента передачи и фазового сдвига от частоты приведены на рис. 2.

Помимо коэффициента передачи по амплитуде при анализе дискретных линейных систем применяют коэффициент передачи по мощности, который равен квадрату коэффициента передачи по амплитуде и иногда задается в

Обратное z – преобразование рациональной функции можно найти, если разложить дробь X ( z ) = A( z )B( z ) и преобразовать её в геометрический ряд

Ввыражении (2) принято, что замкнутый контур интегрирования

представляет собой окружность с центром в начале координат z – плоскости, к которому сходится X ( z ) [1]. Подстановка в формулу (2) z =exp( jω)

9

приводит к тому, что dz заменяется на jzdω, и в качестве замкнутого контура интегрирования можно взять путь по окружности единичного радиуса от точки z = exp( − jπ) до точки z =exp( jπ) (т.е. один оборот по окружности). Следовательно, выражение (2) принимает вид

X ( jw ). Поэтому (3) можно рассматривать как обратное преобразование Фурье.

2.Лабораторное задание

2.1.По согласованию с преподавателем выберете из банка заданий комплексные функции f2(k), g2(k), h2(k).

2.2.Постройте графики модуля и аргумента решетчатой комплексной функции f2(k).

2.3.Постройте графики вещественной и мнимой части решетчатой комплексной функции g2(k).

2.4.Постройте годограф для решетчатой комплексной функции h2(k).

10