Часть 3

СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ

ВЫСШЕЙ МАТЕМАТИКИ

Глава 1

Элементы теории функций

комплексной переменной

1.1. Алгебраическая форма комплексного числа

Комплексным числом называется выражение

,

(1.1)

в котором (действительные числа), атакое число, квадрат которого равен –1,

.

(1.2)

Число называют мнимой единицей.

Выражение называюталгебраической формойкомплексного числа, – действительной частью, а – мнимой частью комплексного числаz. При этом используются обозначения,.

Если , тогда– действительное число. Если, тогда– такое число называют чисто мнимым

Два комплексных числа исчитаются равными, еслии; у = 0. Понятия “больше” и “меньше” для комплексных чисел не существуют.

Комплексное число называется сопряженным по отношению к комплексному числу. Например,. Очевидно, что.

С комплексными числами можно производить арифметические операции (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня). Рассмотрим четыре из перечисленных действий над комплексными числами, записанными в алгебраической форме (1.1).

1) Сложение (вычитание). Чтобы сложить два комплексных числа инужно сложить их действительные и мнимые части

.

(1.3)

Аналогично производится вычитание +

+

Пример 1.1

, .

1) ==;

2) .

2) Умножение:

.

(1.4)

Формула умножения комплексных чисел (1.4) получается, если числа иперемножить как два многочлена и учесть, что. При умножении комплексных чисел удобнее использовать это правило, чем формулу (1.4).

Пример 1.2

= –

–= .

Пример 1.3

В качестве примера, найдем произведение комплексно сопряженных чисел:

= .

Здесь использована формула сокращенного умножения

, в которой принято ,.

Таким образом, произведение сопряженных комплексных чисел равно сумме квадратов действительной и мнимой частей, т.е. равно действительному числу

.

(1.5)

На формуле (1.5) основано построение формулы деления комплексных чисел:

(1.6)

Таким образом, делитель и делимое нужно умножить на комплексное число, сопряженное делителю, тогда в знаменателе будет действительное число. Потом нужно перемножить комплексные числа в числителе.

Пример 1.4

, . Найти:,.

Решение

1) =;

2) =.

Пример 1.5

, найти .

Решение

=

=

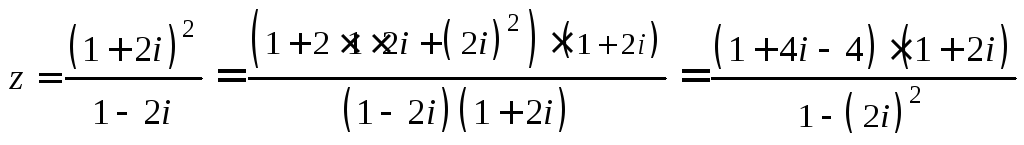Ответ: .

Задачи для самостоятельного решения

1. Выполните действия над комплексными числами и:

1); 2); 3); 4); 5); 6).

Ответы:

1) ; 2); 3); 4); 5); 6).

2. Найдите действительную и мнимую части комплексного числа .

Ответ: = – 0,1;= 1,7.

3. Представить в алгебраической форме комплексное число .

Ответ: .

4. Найдите .

Ответ: .

5. Решите уравнение: .

Ответ: .

1.2 Тригонометрическая форма комплексного числа

Каждому комплексному числу можно сопоставить точку на плоскости. Эта точка будет иметь координаты .

y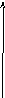

Im z

y

z = x + i y





x

x

0 00O

Re z

Рис.1.1

Соединим начало координат с точкой z. Расстояние от начала координат до точки z называется модулем комплексного числа z и обозначается . Угол(рис.1.1) называется аргументом комплексного числа и обозначается. Если, тогданазывают главным значением аргумента. Все множество аргументов опишется соотношением

,

Нетрудно видеть: ,

Заметим: а) ,

б) ,не определен,

в) ,.

Используя равенства ,, комплексное число z можно записать в виде

(1.7)

Такое выражение называется тригонометрической формой комплексного числа.

Пример 1.6

, найти .

Решение

.

Пример 1.7

Представить в тригонометрической форме комплексное число .

Решение

Из рисунка видно, что ,.

Запишем комплексное число в тригонометрической форме:

.

Пример 1.8

Представить в тригонометрической форме комплексное число

.

Решение

;

.

Таким образом, ,.

Запишем комплексное число в тригонометрической форме:

.