9.2 Пересечение пирамиды плоскостью общего положения

Дано:  - пирамида

Г(МКMN)- о.п.

Построить: Г=m

Построить линию пересечения

пирамиды  плоскостью общего положения Г.

1.Преобразуйте плоскость общего положения в проецирующую, с помощью метода замены плоскостей проекций.

2. Новую плоскость проекций П₄ проведите перпендикулярно заданной плоскости Г

(перпендикулярно горизонтали (MN) заданной плоскости).

3. Ортогонально спроецируйте призму  на новую плоскость проекций П₄ .

4. Спроецируйте плоскость Г на новую плоскость проекций П₄.

Г занимает в системе П₁/П₄ проецирующее положение.

6. Г=m

m = (1-2-3)

5. В системе П₁/П₄ построение линии пересечения пирамиды с плоскостью Г сводится к предыдущей задаче.

6. Затем, получив точки 1₄,2₄,3_4, по линиям проекционной связи найдите их горизонтальные (1₁,2₁,3₁) и фронтальные проекции (1₂,2₂,3₂).

Г=m

m = (1-2-3)

9.3 Пересечение сферы плоскостью

При пересечении сферы плоскостью всегда получается окружность.

Рассмотрим пересечение сферы плоскостью уровня и проецирующей плоскостью.

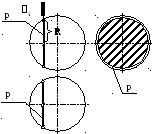
9.4 Пересечение сферы плоскостью уровня

Если секущая плоскость (рис.68) параллельна какой-либо плоскости проекций, то на эту плоскость окружность сечения проецируется без искажения.

На остальные плоскости проекций окружность сечения проецируется в отрезок прямой.

рис. 68

5. ПЕРЕСЕЧЕНИЕ СФЕРЫ ПРОЕЦИРУЮЩЕЙ

ПЛОСКОСТЬЮ

Если секущая плоскость (рис.69) занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (на фронтальной плоскости проекций П₂), окружность сечения изображается отрезком прямой, длина которого равна диаметру окружности.

На остальные плоскости проекций окружность сечения проецируется в эллипсы, которые строят по точкам.

рис. 69

9.6 Построение линии пересечения сферы плоскостью уровня

Дано:  - сфера

Г|| П₁

Построить линию пересечения

m =Г

Фронтальная проекция m₂ - отрезок прямой, совпадает с фронтальной проекцией Г₂ плоскости_.

Горизонтальная проекция линии m₁ - окружность радиусом R.

Профильная проекция линии сечения m₃ вырождается в отрезок прямой.

m₃

Дано:  - сфера

 || П₂

Построить линию пересечения

n = 

Горизонтальная проекция n₁ –отрезок прямой, совпадает с проекцией ₁ плоскости.

Фронтальная проекция линии n₂ – окружность радиусом R.

Профильная проекция n₃ – вырождается в прямую. Замерьте координату «у» на горизонтальной проекции и отложите «у» на профильной проекции.

Дано:  - сфера ( о.п.)

 || П₃

Построить линию пересечения р

 = p

Горизонтальная проекция р₁ и фронтальная проекции р₂ -отрезки прямых.

Профильная проекция р₃ – окружность радиусом R