8.1.2 Теория теплоемкости Дебая

С позиции классической теории теплоемкости нельзя объяснить не только этот вопрос, но и сам факт изменения теплоемкости с температурой. Для объяснения этого факта необходимо принять модель твердого тела, предложенную Дебаем.

Исходя из этой модели можно сделать вывод, что теплоемкость твердого тела должна существенно уменьшаться при понижении температуры кристалла ниже его характеристической (дебаевской) температуры. То есть когда энергия, приходящаяся на одну степень свободы, становится недостаточной для возбуждения высокочастотных фононов. Следовательно, температура, при которой выполняется закон Дюлонга и Пти, должна быть выше характеристической температуры  данного вещества. Значения характеристических температур для некоторых веществ приводятся в таблице 8.3.

Таблица 8.3 - Значения характеристических температур для некоторых веществ

Вещество	, °К
Бериллий	1160
Магний	406
Железо	467
Медь	339
Алюминий	418
Алмаз	~2000
Кремний	658
Германий	366
Свинец	94

О том, что дебаевская температура не является абстракцией, введенной для пояснения квантовых представлений в модели твердого тела Дебая, а характеризует реально существующий параметр твердого тела, можно судить по рисунку 8.2.

И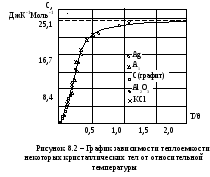сследуя вопрос о внутренней энергии кристаллов, Дебай нашел, что при температурах, близких к абсолютному нулю, внутренняя энергия твердого тела пропорциональна четвертой степени абсолютной температуры

,

где а - постоянный множитель, зависящий от природы кристалла.

Из этого соотношения можно найти выражение для теплоемкости

.

Следовательно, вблизи абсолютного нуля теплоемкость твердого тела пропорциональна кубу абсолютной температуры. Эта закономерность носит название закона кубов Дебая.

Область применения закона кубов лежит ниже температуры, равной /50. При более высоких температурах от /50 до  находится промежуточная область, для которой количественная связь между теплоемкостью и температурой определяется для каждого конкретного вещества отдельно. Выше характеристической температуры , как указывалось ранее, теплоемкость твердого тела не зависит от температуры (закон Дюлонга и Пти).

Опытные исследования теплоемкостей различных кристаллических тел при низких температурах показали, что закон кубов Дебая оправдывается не для всех кристаллов, а только для таких, для которых атомы в кристаллической решетке связаны со своими соседями примерно одинаково прочно во всех трех направлениях. Для слоистых кристаллов типа графита, в которых силы связи между соседними атомами внутри слоя значительно больше сил связи между ближайшими атомами из двух соседних слоев, теплоемкость при температурах, близких к абсолютному нулю, оказывается пропорциональной квадрату абсолютной температуры. Обнаружены и такие кристаллы, для которых теплоемкость около абсолютного нуля пропорциональна первой степени температуры. Такие кристаллы имеют нитевидное строение. Силы связи внутри нити много больше, чем между соседними нитями.

Теория Дебая приводит к выводам, которые хорошо совпадают с экспериментальными данными в широком интервале температур, но и она не свободна от недостатков. Трудно, например, согласиться с тем, что энергия кристалла отождествляется с энергией стоячих волн. В стоячей волне узлы и пучности закономерно распределены в пространстве, поэтому исключается возможность тепловых флуктуаций, совершенно неизбежных при тепловом движении.

Дебаевская модель твердого тела является упрощенным представлением твердого тела в виде изотропной упругой среды, способной совершать колебания в конечном интервале частот. Поэтому и выводы этой теории (например, зависимость теплоемкости от температуры) хорошо совпадают с экспериментальными данными только для кристаллов с простыми решетками. К телам сложной структуры теория Дебая неприменима, так как энергетический спектр колебаний таких тел оказывается чрезвычайно сложным. В молекулярных кристаллах, например, кроме поступательно-колебательного движения молекулы как целого, приходится учитывать ее вращательные колебания и колебания атомов или групп атомов внутри молекулы.