§10. Вероятность попадания в заданный интервал показательно распределенной случайной величины.

Найдем вероятность попадания в интервал (a, b) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения: F(x) = 1 – e ^{– x} (x  0)

Используем формулу: P(a < X < b) = F(b) – F(a).

Учитывая, что F(a) = 1 – e ^{– a}, f(b) = 1 – e ^{– b}, получим

P(a < X < b) = e^−a – e^−b. (1)

Значения функции e ^{– x} находят по таблице.

§12. Числовые характеристики показательного распределения.

Пусть непрерывная случайная величина X распределена по показательному закону

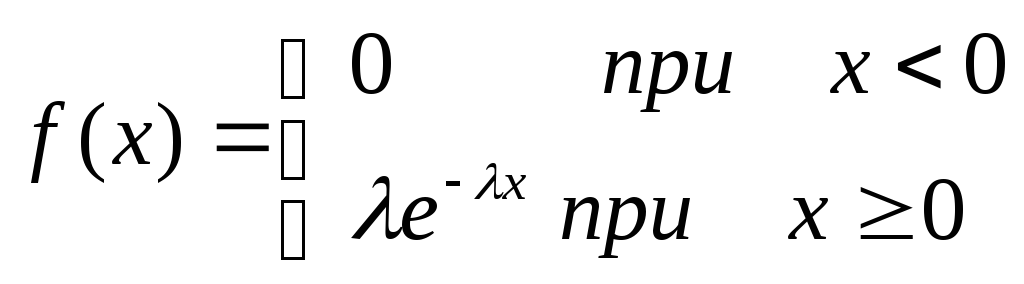
Найдем математическое ожидание:

М(X) = =

Интегрируя по частям, получим

M(X) = 1/ (2)

Таким образом, математическое ожидание показательного распределения равно обратной величине параметра .

Найдем дисперсию:

D(X) = – [M(X)]² = – 1/².

Интегрируя по частям, получим = 2/².

Следовательно, D(X) = 1/².

Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:

(X) = 1/ (3)

Сравнивая (3) и (2), заключаем, что M(X) = (X) = 1/,

т.е. математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Замечание 1. Пусть на практике изучается показательно распределенная случайная величина, причем параметр  неизвестен. Если математическое ожидание также неизвестно, то находят его оценку (приближенное значение), в качестве которой принимают выборочную среднюю . Тогда приближенное значение параметра находят с помощью равенства

* = 1/

Замечание 2. Допустим, имеются основания предположить, что изучаемая на практике случайная величина имеет показательное распределение. Для того чтобы проверить эту гипотезу, находят оценки математического ожидания и среднего квадратического отклонения, т.е. находят выборочную среднюю и выборочное среднее квадратическое отклонение. Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой, поэтому их оценки должны различаться незначительно. Если оценки окажутся близкими одна к другой, то данные наблюдений подтверждают гипотезу о показательном распределении изучаемой величины; если же оценки различаются существенно, то гипотезу следует отвергнуть.

Показательное распределение широко применяется в приложениях, в частности в теории надежности, одним из основных понятий которой является функция надежности.

§11. Геометрические вероятности

Геометрические вероятности − это вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений:

1) поставленная точка может оказаться в любой точке отрезка L;

2) вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L.

В этих предположениях вероятность попадания точки на отрезок l определяется равенством:

Р = Длина l/Длина L.

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством

Р = Площадь g/Площадь G.