Тема 3. Случайные величины

+ §1. Дискретные случайные величины

Рассмотрим переменную X, которая принимает свои отдельные значения x с некоторой вероятностью p.

Определение. Случайной величиной X называется действительная функция X(x), определенная на множестве всех исходов опыта, обладающего статистической устойчивостью.

Случайные величины делятся на дискретные (или прерывные) и непрерывные.

Определение. Случайная величина X называется дискретной, если множество ее значений {x₁, x₂, x₃, …,x_n …} конечно или счетно.

Примером дискретной случайной величины может служить число пассажиров автобуса при его движении по маршруту.

Под законом распределения случайной величины понимается соответствие между значениями случайной величины и вероятностями, с которыми эти значения принимает случайная величина. Для дискретной случайной величины закон распределения задается в виде таблицы

Таблица 1

Значения случайной величины xi	x1	x2	x3	…	xn	…
Вероятности значений pi	p1	p2	p3	…	pn	…

В первой стоке этой таблицы значения x_i случайной величины, во второй вероятности p  0 и сумма их равна 1, т.е.

p₁ + p₂ + p₃ + … + p_n + … = 1

Если две случайные величины X и Y определены на одном множестве исходов опыта, то для них определены алгебраические операции: X + Y, CX (С – постоянное число), XY. Произведение случайной величины X на постоянную величину С – это есть новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные произведению на С значений случайной величины X.

+ §2. Числовые характеристики дискретных случайных величин

Пусть закон распределения дискретной случайной величины задан таблицей

xi	x1	x2	x3	…	xn	…	(3)
pi	p1	p2	p3	…	pn	…

Определение. Сумма

(4)

называется математическим ожиданием дискретной случайной величины и обозначается M(X).

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно этой постоянной, т.е. M(C) = C.

2. Постоянный множитель можно выносить за знак математического ожидания, т.е. M(CX) = C M(X).

3. Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий

M(X + Y) = M(X) + M(Y)

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X)  M(Y)

Определение. Дисперсией D(x) случайной величины X называется математическое ожидание случайной величины [X – M(X)]², т.е.

D(X) = M[X – M(X)]², (5)

Разность X – M(X) – это есть отклонение случайной величины X от своего математического ожидания. Поэтому дисперсия случайной величины X согласно (5) – это есть математическое ожидание квадрата отклонения ее от математического ожидания. Пусть M(X) = a. Тогда формулу (5) более подробно можно записать следующим образом:

D(X) = (x₁ – a)²  p₁ + (x₂ – a)²  p₂ + … + (x_n – a)²  p_n + … (6)

Свойства дисперсии:

1. Дисперсия постоянной равна нулю, т.е. D(X) = 0.

2. Постоянный множитель можно выносить за знак дисперсии, т.е.

D(CX) = C² D(X)

3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий, т.е.

D(X + Y) = D(X) + D(Y)

Определение. Средним квадратическим отклонением _x случайной величины X называется корень квадратный из ее дисперсии

(7)

+ §3. Функция распределения случайной величины. Непрерывные случайные величины.

Задать случайную величину можно также с помощь так называемой функции распределения. Рассмотрим случайную величину X. Пусть x ее отдельное значение. Тогда {X < x} – будет означать событие, что случайная величина X примет значение меньше x.

Определение. Функция распределения F(x) случайной величины X выражает вероятность того, что X примет значение меньше x, т.е.

F(x) = P(X < x) (1)

Свойства функции распределения:

1. F(– ) = 0;

2. F(+ ) = 1 (так как X < +  означает, что случайная величина X принимает все значения, а вероятность такого события равна 1);

3. Согласно своему определению функция распределения F(x) выражает вероятность и поэтому 0  F(x)  1;

4. Вероятность попадания случайной величины X в промежуток [a, b] определяется формулой P(a  X < b) = F(b) – F(a) (2)

Существуют случайные величины, множество значений которых заполняет некоторый числовой промежуток. Такие случайные величины можно задать с помощью функции распределения. Если функция F(x) распределения случайной величины X непрерывна и имеет почти всюду непрерывную производную, то случайную величину X называют непрерывной. Производная F’(x) функции F(x) называется плотностью вероятности случайной величины X и обозначается f(x). Таким образом, плотность вероятности случайной величины X – это есть f(x) = F’(x).

Непосредственно из определения плотности вероятности случайной величины X вытекают следующие ее свойства:

1. f(x)  0;

2. ;

3. 

4. 

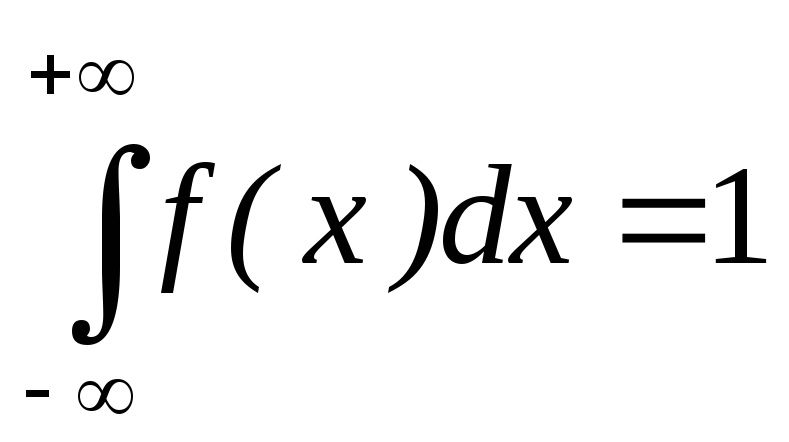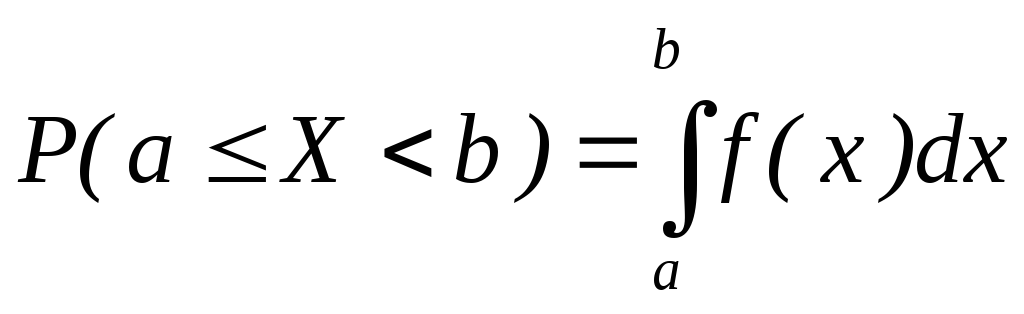
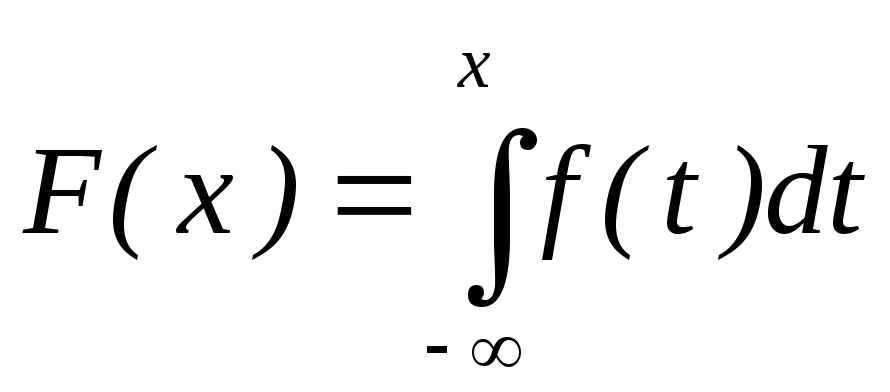
Вероятность того, что непрерывная случайная величина примет конкретное значение, равна нулю.

Математическим ожиданием непрерывной случайной величины X называется число, определяемое равенством

Дисперсия D(x) непрерывной случайной величины X определяется по формуле:

+ §4. Нормальное распределение.

Говорят, что случайная величина X распределена по нормальному закону, если ее плотность вероятности равна

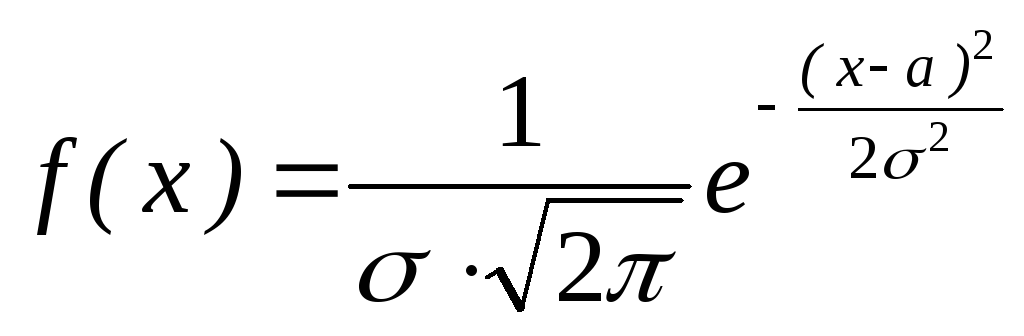
Для случайной величины X распределенной по нормальному закону:

M(X) = a, D(X) =  ², _x = 

Функция распределения нормально распределенной величины имеет вид

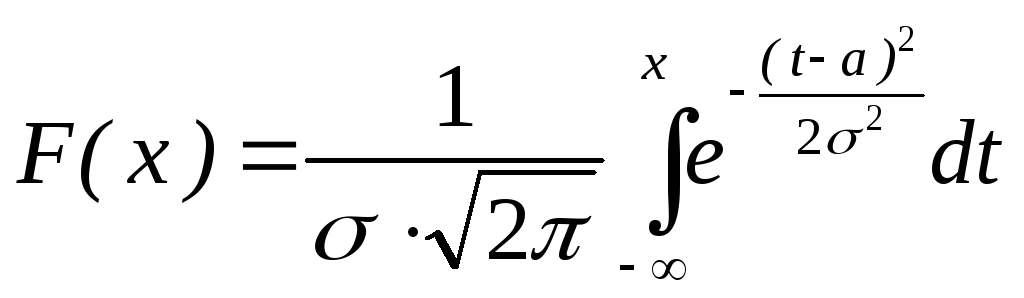
Известно, что если случайная величина X задана плотностью вероятности F(X), вероятность того, что X примет значение, принадлежащее интервалу (a, b), равна

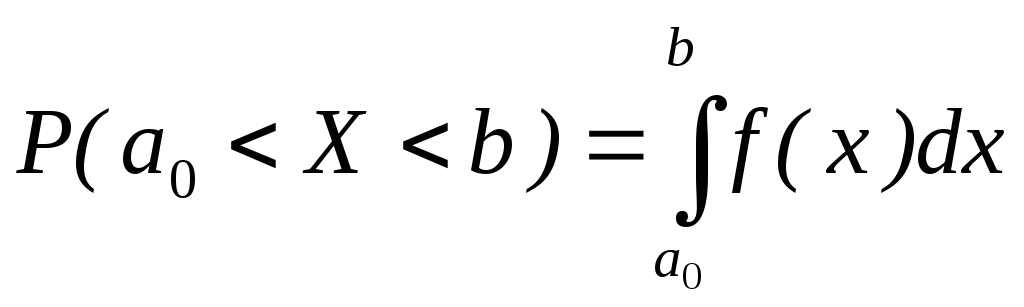
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (а, b), равна

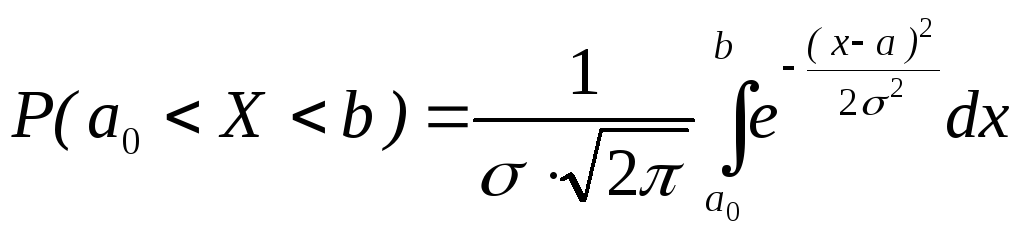
Эту формулу, пользуясь функцией Лапласа

можно записать в следующем удобном для вычислений виде:

(3)

+ §5. Нормальная кривая.

Исследуем функцию

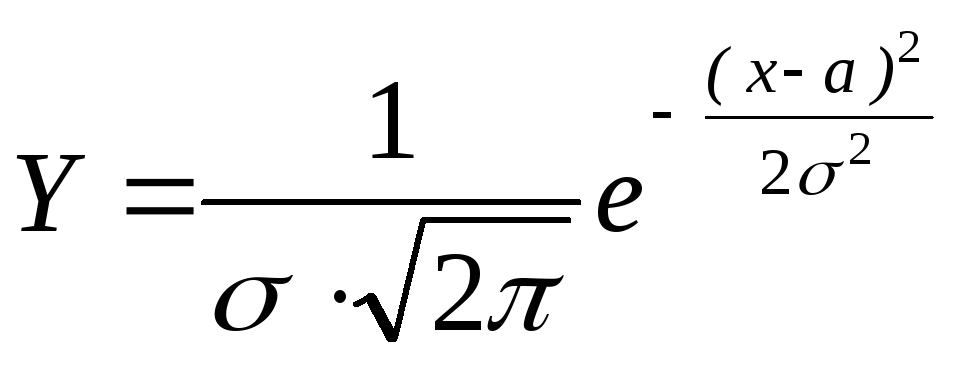
которая задает плотность вероятности нормального закона распределения случайной величины X. График этой функции называется нормальной кривой (кривой Гаусса). Рассмотрим свойства этой функции.

1. Функция определена на всей числовой оси x.

2. При всех значениях x функция принимает положительные значения, нормальная кривая расположена над осью x.

3. Предел функции при неограниченном возрастании x (по абсолютной величине) равен нулю, т.е. ось x служит горизонтальной асимптотой графика.

4. Исследуем функцию на экстремум. Найдем производную

Первый сомножитель обращается в нуль приx = a. Поэтому y = 0 при x = a, Y > 0 при x < a, Y < 0 при x > a. Следовательно, при x = a функция имеет максимум, равный .

5. Функция содержит разность (x – a) в квадрате, т.е. график функции симметричен относительно прямой x = a.

+ §6. Правило трех сигм.

Выше была рассмотрена формула P(|X – a| < ) = 2 Ф .

Преобразуем эту формулу, положив = t и, следовательно,   t. В результате будем иметь P(|X – a| <  t) = 2Ф(t).

Таким образом, значение функции 2Ф(t) при заданном t определяет вероятность того, что отклонение нормально распределенной случайной величины по абсолютной величине будет меньше числа t.

Например, если t = 1 и, следовательно, t = , то

P(|X – a| < ) = 2Ф(1) = 20,3413 = 0,6826.

т.е. вероятность того, что отклонение по абсолютной величине будет меньше среднего квадратического отклонения, равна 0,6826.

Положим теперь t = 3. Тогда t = 3, и поэтому будем иметь

P(|X – a| < 3) = 2Ф(3) = 20,4965 = 0,9973

т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что отклонение по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев такое событие может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена по нормальному закону, то отклонение этой величины от математического ожидания (по абсолютной величине) не превосходит утроенного среднего квадратического отклонения. На основании сформулированного правила трех сигм в статистике часто пролагают, что относительная частота не может отклониться (по абсолютной величине) от вероятности более чем на три сигмы.

+ §7. Законы биномиальный и Пуассона.

Биномиальным называют закон распределения B(n, p) дискретной случайной величины X – числа появлений событий в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения X = k (числа k появлений события) вычисляют по формуле Бернулли:

Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют приближенную формулу

Где k – число появлений события в n независимых испытаниях,  = np (среднее число появлений события в n испытаниях), и говорят, что случайная величина распределена по Закону Пуассона P().