Теория вероятностей (для студентов специальности «Информатика») Тема 2. Повторные независимые испытания

§1. Формула Бернулли.

Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами: событие А осуществилось и не осуществилось , причем вероятность этих исходов не меняется от испытания к испытанию. Вероятность наступления событияА в каждом испытании обозначим через р, т.е. Р(А) = р. Тогда Р()= 1 – р = q. Пусть m – число (частота) наступления события А в n испытаниях. Обозначим через Р_m, n – вероятность того, что частота появления события А равна именно m . Эта вероятность может быть посчитана по формуле Бернулли

(1)

Числа Р_m,n также интерпретируется как вероятность иметь ровно m осуществлений события А в n независимых испытаниях с двумя исходами. Вероятность того, что частота m появления события А в n испытаниях примет значение из промежутка [m₁, m₂] (m₁  m  m₂) равна

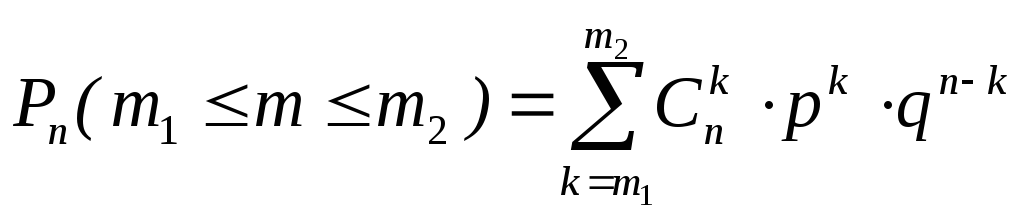(2)

Вероятность того, что событие А хотя бы один раз наступит в n испытаниях вычисляется по формуле

Р _n (m  1) = 1 – Р _0,n = qⁿ

§2. Формула Пуассона.

Нередко приходится рассматривать эксперименты с большим числом испытаний. Нетрудно видеть, что для больших n и m вычисление вероятностей по формуле Бернулли представляется значительные затруднения, становятся очень громоздкими. В этом случае применяются приближенные формулы, позволяющие с достаточной степенью точности найти эти вероятности. Если число испытаний достаточно велико, а р мало и при этом произведение np – не больше 10, то вероятность Р_{m, n} можно найти по формуле Пуассона

(3)

Вычисления по формуле (3) существенно упрощаются, если используются специальные таблицы.

Замечание. Вероятность того, что в испытаниях событие наступит: а) менее k раз ; б) более k раз; в) не менее k раз; г) не более k раз, – находят соответственно по формулам:

а) Р_{0, n} + Р_{1, n} + … + Р _{k–1, n}.

б) Р_{k+1, n} + Р _{k+2, n} + … + Р_{n, n}.

в) Р_{k, n} + Р_{k+1, n} + … + Р_{n, n}.

г) Р_{0, n} + Р_{1, n} + … + Р_{k, n}.

§3. Локальная и интегральная теоремы Муавра-Лапласа.

Рассмотрим вопрос о вычислении вероятности наступления события А ровно m раз в n независимых испытаниях, когда m и n достаточно велики и выполняется условие npq  20.

Локальная теорема Муавра-Лапласа. Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Р_{m, n} того, что в n независимых испытаниях событие А наступит m раз, находится по формуле

(4)

где (q = 1 – p)

а функция f(x) определяется равенством

(5)

Формула (4) называется локальной формулой Муавра-Лапласа. С возрастание n относительная точность значений вероятностей Р, получаемых по ней, возрастает. Значения функции f(x), заданной формулой (5), находят по таблице. Следует также иметь в виду:

1. Функция f(x) является четной, т.е. f(–x) = f(x). Поэтому в таблице приведены значения функции (5) лишь для положительных значений аргумента.

2. Функция f(x) монотонно убывает при положительных значениях x, а предел ее при x   равен нулю.

3. Если x  5, то можно считать приближенно, что f(x) = 0.

Интегральная теорема Муавра-Лапласа. Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях число наступлений события А окажется заключенным в границах от m₁ до m₂ включительно (m₁  m₂), находится по формуле

P_n (m₁  m  m₂) = Ф(x₂) – Ф(x₁) (6)

где ,

а 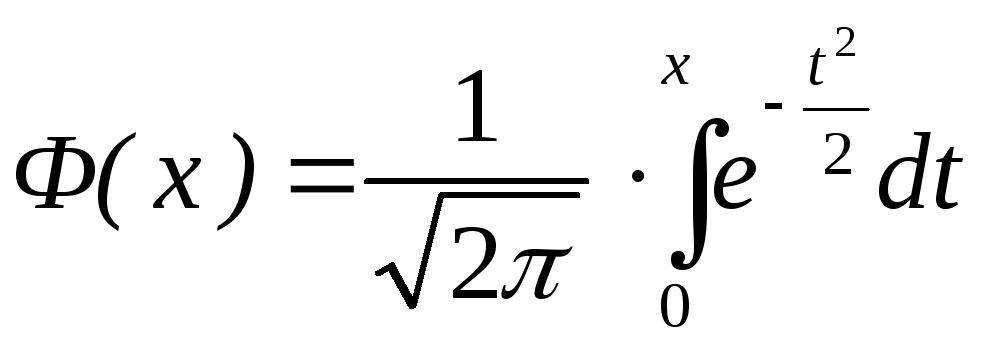(7)

и называется функцией Лапласа, значение которой находится по таблице.

Формула (6) называется интегральной формулой Муавра-Лапласа.. Функция Лапласа Ф(x) обладает следующими свойствами:

1. Функция Ф(x) – нечетная, т.е. Ф(–x) = – Ф(x).

2. Функция Ф(x) – монотонно возрастающая.

3. Предел функции Ф(x) при x   равен единице.

4. Для всех значений x  5 можно считать приближенно Ф(x) = 1.

Из интегральной теоремы Муавра-Лапласа вытекает важное для приложений следующее следствие:

Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях абсолютная величина отклонения числа m наступлений события А от произведения np не превзойдет положительного числа  , находится по формуле

(8)

Из формулы (8) в свою очередь можно получить формулу оценки отклонения частоты m/n появления события А в n испытаниях от вероятностей р:

(9)