чания итераций следует убедиться в малости значения f (c) . В противном
случае найденное значение c следует считать точкой разрыва функции. Тем не менее, гарантированная сходимость обеспечивает методам по-
ловинного деления и ложного положения достаточно широкую область применения. Например, многие программы решения нелинейных уравнений начинают вычисления методом половинного деления, а затем, когда корень локализован в достаточно узкой области, уточняют его быстро сходящимся методом.
Метод Ньютона и метод секущих
Метод Ньютона является, пожалуй, самым популярным методом решения нелинейных уравнений. В нем для вычисления каждого следующего приближения к корню используется экстраполяция функции с помощью
касательной к кривой в текущей точке. |
|
|
Пусть xn – текущее приближение корня xr и |
x = xr − xn . Тогда можно |
|
записать следующее разложение функции f (x) в ряд Тейлора |
||
f (xr )= f (xn + x)= f (xn )+ f ′(xn ) |
x + |
1 f ′′(xn ) x2 +… |
|
|
2 |
С учетом того, что f (xr )= 0 , получим |
|
|
f (xn )+ f ′(xn ) x + 1 f ′′(xn ) |
x2 |
+…= 0 |
2 |
|
|
Выражение (3.5) представляет собой одну из форм записи уравнения (3.1). она удобна тем, что можно находить приближенные решения, ограничиваясь конечным числом слагаемых в левой части (3.5). с учетом двух слагаемых находим приближение вида
|
|
x(1) = x(1) |
− x = − |
f (xn ) |
|
|
|
f ′(xn ) |
|||
|
|
r |
n |
||
|
|
|
|
||
Если теперь точку |
x(1) |
взять в качестве следующего за x уточнения корня, |
|||
|
r |
|
|
|
n |
то получим итерационную формулу метода Ньютона:
x |
= x |
− |
f (xn ) |
. |
(3.6) |
|
|||||
n+1 |
n |
|
f ′(xn ) |
|
|
22
Итерационный процесс по формуле (3.6) продолжается до тех пор, пок разность xn+1 − xn не достигнет заданной погрешности решения или значе-
ние f (xn+1 ) не уменьшится до заданной величины.
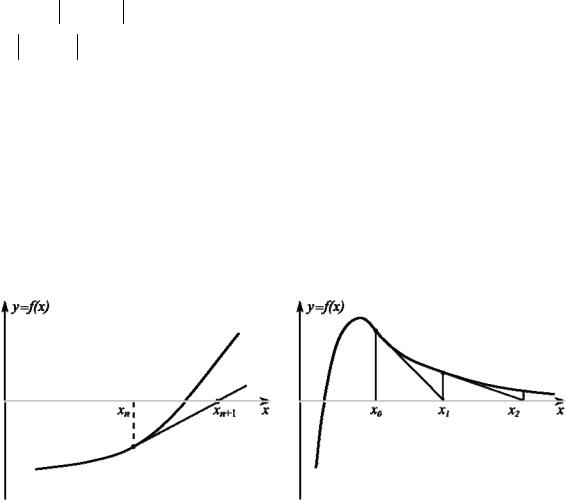
Нетрудно показать, что геометрически xn+1 интерпретируется как точка пересечения оси X касательной к кривой y = f (x) в точке xn (рис. 3.4).
Отсюда и второе название метода Ньютона – метод касательных. Совершенно очевидно, что сходимость метода в большей мере зависит от удачного выбора начального приближения x0 . На рис.3.5 приведена ситуация, когда итерации по методу Ньютона уводят от корня уравнения. Можно представить и другие случаи, например, осцилляции последовательных приближений в окрестности точки, не являющейся корнем.
Рис. 3.4. Метод Ньютона |
Рис. 3.5. Расходимость метода |
|
Ньютона |
Тем не менее, если начальное приближение выбрано в ближайшей окрестности корня, то метод обеспечивает очень быструю, квадратичную сходимость итерационного процесса. Именно это свойство придает методу Ньютона особое значение.
Однако помимо возможных затруднений с выбором начального приближения у метода Ньютона есть еще один недостаток – необходимость задания производной f ′(x) в аналитической форме. Если функция f (x) сложна, то аналитическое дифференцирование сопряжено со значительными трудностями. Еще большие проблемы возникают, когда f (x) вообще не задана аналитически, например, ее значения являются результатом
23
вычислений по некоторому алгоритму. Этот недостаток несколько ограничивает область практического применения метода Ньютона.
Проблему аналитического задания производной можно обойти, если в формуле (3.6.) воспользоваться разностным предтавлением производной f ′(xn )
f ′(xn )≈ f (xn )− f (xn−1 ). xn − xn−1
Тогда получим формулу
x |
= x |
− f (x |
) |
xn |
− xn−1 |
|
, |
(3.7) |
||
|
|
) |
||||||||
n+1 |
n |
n |
|
f (x |
)− f |
(x |
|
|
||
|
|
|
|
n |
|
|
n−1 |
|
|
|
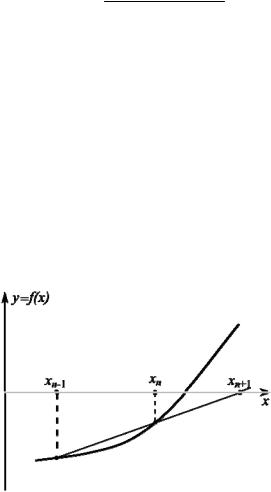
составляющую основу метода секущих. Геометрическая интерпретация одного шага итераций дана на рис. 3.6. Как и в методе Ньютона, вычисления заканчиваются, когда разность между последовательными значениями xn и xn+1 становится меньше заданной точности или когда значение
f (xn+1 ) становится достаточно близким к нулю.
Рис. 3.6. Метод секущих
Проблема выбора начального приближения для метода секущих столь же актуальна, что и для метода Ньютона. Причем, в отличие от метода Ньютона (3.6), использующего для вычисления xn+1 только одно предыдущее приближение xn и поэтому являющегося одношаговым, метод секущих, как это следует из формулы (3.7), двухшаговый метод. Для начала поиска корня теперь требуется уже не одна точка x0 , а две – x0 и x1 . Однако это усложнение задачи не является существенным, как правило, если
24
выбор точки x0 обеспечивает сходимость метода Ньютона, то за x1 можно взять любую близкую к x0 точку.
Скорость сходимости итерационного процесса (3.7) ниже, чем у итераций по методу Ньютона. Тем не менее, она достаточно высока для того, чтобы обеспечить методу секущих широкую область применения. Cовременные компьютерные программы часто основаны на полиалгоритмах, представляющих собой комбинации двух и более методов. Например, в начале используется метод половинного деления и вычисления ведутся до тех пор, пока приближение не окажется настолько близко к корню, что будет сходиться метод секущих. После этого для ускорения сходимости вычисления продолжаются методом секущих.
25