
- •ВВЕДЕНИЕ
- •1. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
- •ЗАДАНИЯ
- •2. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- •ЗАДАНИЯ
- •3. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ ИТЕРАЦИОННЫМИ МЕТОДАМИ
- •Методы простой итерации
- •Метод половинного деления и ложного положения
- •Метод Ньютона и метод секущих
- •ЗАДАНИЯ
- •4. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
- •Метод Ньютона
- •Метод последовательной параболической интерполяции
- •Метод золотого сечения
- •Задания
- •5. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •Задания №5
- •6. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ НЬЮТОНА
- •Метод простой итерации
- •Метод Ньютона
- •Задания
2.ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Снеобходимостью вычисления определенных интегралов вида
I = ∫b f (x)dx
a
приходится сталкиваться при решении многих физических задач. При этом подынтегральная функция f (x) обычно определяется одним из трех способов:
1.Задается явная формула для f (x).
2.Функция f (x) явно не задана, но ее значения могут быть рассчита-
ны для любых значений аргумента из отрезка [a, b]. Это можно сделать, например, путем реализации некоторого вычислительного алгоритма.
3. Функция f (x) задается таблично, часто по результатам экспери-
мента.
В первом случае интегралы иногда удается вычислить аналитически, а во втором и третьем – задача интегрирования решается лишь численными методами. К численным методам прибегают и тогда, когда интеграл от явно заданной функции не выражается через элементарные или специальные функции.
Пусть f (x) – ограниченная на отрезке [a, b] функция. Тогда наиболее
часто применяемый метод численного интегрирования состоит в том, что интеграл заменяется некоторой линейной комбинацией значений f (xi ) , вычисленных в n +1 точке отрезка [a, b]:
b |
n |
|
I = ∫ f (x)dx ≈ ∑Ai f (xi ) . |
(2.1) |
|
a |
i=0 |
|
Приближенное равенство (2.1) называется квадратурной формулой, коэффициенты Ai – квадратурными коэффициентами, а точки xi – узлами квадратурной формулы.
Большинство квадратурных формул получается путем замены подынтегральной функции на всем отрезке интегрирования или на его частях на более простую функцию f (x) , интегрируемую аналитически и прини-
мающую в узлах квадратурной формулы значения f (xi ) = f (xi ) . В качест-
8
ве f (x) можно взять полиномы, кусочные полиномы, тригонометрические, экспоненциальные и другие функции. Конкретный выбор аппроксимирующей функции f (x) может зависеть от вида подынтегральной функции f (x) или определяться физическим содержанием решаемой задачи.
Важной особенностью квадратурной формулы является положение ее узлов. В ряде формул узлы следуют друг за другом с постоянным шагом, в других – выбор узлов основан, например, на соображениях максимальной точности.
Рассмотрим наиболее распространенные квадратурные формулы. К ним относятся формулы Ньютона-Котеса.
Формулы Ньютона-Котеса. Выберем на отрезке [a, b] с постоянным шагом n +1 узел интерполяции x0 = a, x1 = a + h, ..., xn =b и построим
интерполяционный полином Pn (x) . Положив f (x) = Pn (x) и проведя интегрирование, получим группу формул Ньютона-Котеса. Формулы, принадлежащие этой группе, различаются числом квадратурных узлов.
Для определения вида квадратурных коэффициентов Ньютона-Котеса полином Pn (x) удобно представить в форме Лагранжа:
n
Pn (x) = ∑ f (xi )Li (x) .
i=0
Тогда формальная процедура интегрирования приводит к выражению
b |
n |
b |
I ≈ ∫Pn (x)dx = ∑ f (xi )∫Li (x)dx . |
||
a |
i=0 |
a |
Сравнивая его с выражением (2.1), мы находим общий вид квадратурных коэффициентов в формулах Ньютона-Котеса:
Ai = ∫b |
Li (x)dx . |
(2.2) |
a |
|
|
Простейшей из формул Ньютона-Котеса является формула прямо-
угольников, соответствующая интерполяции подынтегральной функции
полиномом нулевой степени – константой. Для вычисления единственного
квадратурного коэффициента этой формулы в выражении (2.2) следует положить L0 (x) =1. После чего находим A0 =b −a и формула прямоугольников записывается в виде
9
R( f ) = (b −a) f (a) .
Далее в группе формул Ньютона-Котеса следует формула трапеций,
являющаяся результатом интерполяции функции f (x) полиномом первой
степени по узловым точкам x0 = a, |
x1 = a + h =b . В этом случае полиномы |
||||||
Лагранжа имеют вид |
|
|
|
|
|
|
|
L |
(x) = − |
x − x1 |
, |
L |
(x) = |
x − x0 |
. |
|
|
||||||
0 |
|
h |
|
1 |
|
h |
|
|
|
|
|
|
|||
Вычисления интегралов (2.2) дают значения A0 = A1 = h 2 , и формула трапеций записывается как
2 , и формула трапеций записывается как
T ( f ) = h [f (x0 ) + f (x1)] . |
(2.3) |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
Пусть теперь подынтегральная функция интерполируется по узлам |
||||||||||
x0 = a, x1 = a + h, x2 = a + 2h =b . |
Квадратичный интерполяционный |
по- |
||||||||
линомом P2 (x) выражается через три полинома Лагранжа |
|
|||||||||
L |
(x) = |
1 |
|
(x − x )(x − x |
), |
|
||||
|
|
|||||||||
0 |
|
|
2h2 |
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
||||
L (x) = − |
1 |
|
|
(x − x |
)(x − x |
), |
|
|||
|
|
|
|
|||||||
1 |
|
|
|
h2 |
0 |
2 |
|
|||
|
|
|
|
|
|
|
|
|||
L |
(x) = |
1 |
|
|
(x − x |
)(x − x ) . |
|
|||
|
|
|
||||||||
2 |
|
2h2 |
0 |
1 |
|
|
||||
|
|
|
|
|
|
|
||||
Использование этих выражений в интегралах (2.2) позволяет получить следующие значения квадратурных коэффициентов
A = A = 1 h , |
A = 4 h |
|
|||
0 |
2 |
3 |
1 |
3 |
|
|
|
|
|
||
и записать формулу |
|
|
|
|
|
S( f ) = h |
[f (x0 ) + 4 f (x1) + f (x2 )]. |
(2.4) |
|||
3 |
|
|
|
|
|
Она называется формулой Симпсона или формулой парабол.
Продолжая и далее эту процедуру построения квадратурных формул,
можно получить, в частности, формулу «трех восьмых»
V ( f ) = 38h [f (x0 ) +3 f (x1) +3 f (x2 ) + f (x3 )]
10

и формулу Боде |
|
|
C( f ) = |
2h |
[7 f (x0 ) +32 f (x1) +12 f (x2 ) +32 f (x3 ) + 7 f (x4 )] . |
|
45 |
|
Оценим теперь погрешности, возникающие при использовании описанных выше квадратурных формул. Так как во всех из них в качестве приближенного значения интеграла берется интеграл от интерполяционного полинома, то допускаемая при этом ошибка есть
E = ∫b [f (x) − Pn (x)] dx .
a
Можно показать, что с учетом погрешности интерполяции это равенство принимает вид
|
1 |
|
b |
)(x − x )...(x − x ) f (n+1) |
|
|
|
E = |
|
(x − x |
(z(x))dx , |
(2.5) |
|||
|
|
||||||
|
(n + |
0 |
1 |
n |
|
|
|
|
1)!∫a |
|
|
|
|
||
где z(x) – зависящая от x точка отрезка [a,b]. Применим оценку (2.5) к конкретным квадратурным формулам. При этом будем считать, что производ-
ные ограничены значениями Mn = max f (n) (x) .
a≤x≤b
В случае формулы прямоугольников n = 0, |
x0 = a, |
b = a + h и оценка |
||||||||||||||||||
погрешности преобразуется к виду |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
a+h |
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ER |
|
= |
′′ |
|
|
≤ |
|
h |
2 |
. |
|
|
|
(2.6) |
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
∫ (x −a) f (z(x)) dx |
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||
А для формулы трапеций (2.3) при n =1, |
x0 = a, |
|
|
x1 =b = a + h |
из (2.5) мы |
|||||||||||||||
находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
a+h |
′′ |
|
|
|
|
|
M2 |
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ET |
= |
|
∫ |
(x −a)(x − a − h) f |
|
dx |
≤ |
h |
. |
(2.7) |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
(z(x)) |
|
12 |
|
|||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Несколько более сложные преобразования дают для оценки погрешности
формулы Симпсона неравенство
ES |
|
≤ |
M4 |
h5 . |
(2.8) |
|
|
||||||
90 |
||||||
|
|
|
|
|
11

Во все приведенные оценки (2.6)–(2.8) входят степени величины шага h. Если эта величина не мала, то не следует ожидать значительной точности вычисления интеграла. На практике малость шага h можно обеспечить двумя способами. Один из них состоит в увеличении числа узлов n+1 квадратурной формулы. Тогда при фиксированной длине отрезка [a,b] шаг
уменьшается как (b −a) / n и можно ожидать достижения приемлемой точ-
ности интегрирования. Однако при этом приходится применять формулу Ньютона-Котеса, основанную высокой степени интерполяционного полинома. Как показывают детальные исследования, при степени полинома выше десятой часть квадратурных коэффициентов принимает отрицательные значения, и возникают проблемы, связанные с ошибками округления. Поэтому формулы с большим числом квадратурных узлов на практике применяют редко. Предпочтение отдают формулам низкого порядка.
Второй способ уменьшения шага заключается в том, что отрезок ин-
тегрирования [a,b] делится на несколько частей. Затем на каждой отдельно
взятой части применяется избранная квадратурная формула и результаты суммируются. Таким образом в вычислительную практику вводятся так называемые составные формулы. Как нетрудно показать составные фор-
мулы прямоугольников, трапеций и Симпсона при фиксированном шаге h
имеют вид
|
|
|
n−1 |
|
|
|
|
RS ( f ) = h∑ f (xi ) , |
|
|
|
||||
|
|
|
i=0 |
|
|
|
|
|
|
( f ) = h |
n−1 |
|
|
|
|
TS |
∑[f (xi ) + f (xi+1)] , |
|
|
||||
|
|
2 i=0 |
|
|
|
|
|
S |
|
( f ) = h |
n−1 f (x ) + 4 f ((x + x |
) 2)+ f (x |
) . |
||
|
S |
3 |
∑i=0 |
i |
i i+1 |
i+1 |
|
Вследствие суммирования ошибок, допускаемых на каждом из подынтервалов полного интервала интегрирования, точность составных формул на порядок ниже точности основных. Таким образом, из оценок (2.6)–(2.8) следует, что составные формулы прямоугольников и трапеций имеют первый и второй порядок точности, в то время как составная формула Симпсона – четвертый порядок. В силу этой относительно высокой точности составная формула Симпсона особенно часто используется в практике численного интегрирования. Однако следует иметь в виду, что составная формула Симпсона использует нечетное число квадратурных уз-
12
лов. Если по каким-либо причинам это условие выполнить не удается, то можно применять имеющую тот же порядок точности составную формулу «трех восьмых».
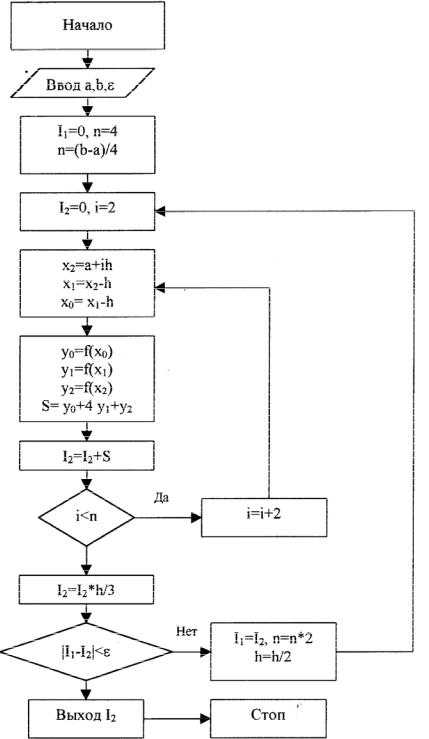
Рис. 2.1. Блок-схема метода Симпсона
На практике при вычислении интегралов теоретические оценки погрешностей используются редко, т.к. они связаны с трудоемкими оценками
13

производных. Поэтому часто применяется следующий способ. Вычисляется значение интеграла I1 при некоторой величине шага h. Затем шаг уменьшается вдвое (или в N-раз) и вычисляется значение интеграла I2 . Пусть требуется вычислить значение интеграла с точностью ε . Тогда проверяется условие I1 − I2 <ε . Если это условие выполняется, то I2 прини-
мается за искомое значение интеграла; если же оно не выполняется, то последнее полученное значение I2 считается предыдущим, т.е. I1 ← I2 . После чего шаг уменьшается и вычисляется новое значение I2. Процесс уменьшения шага продолжается до тех пор, пока модуль разности I1 и I2 не станет меньше ε .
14
