28. Криволінійні кординати.

До цього часу ми мали справу з декартовими або косокутними координатами. Положення точки зручно визначити за допомогою криволінійних координат.

-92-

Три координати називаються криволінійними координатами точки, якщо вони однозначно визначають положення точки в просторі.

Вони вводяться за допомогою системи рівнянь

/28.1/

Тобто

/28.1/

Рівняння /28.1/ можна розв’язати відносно

Функції /28.1/ і /28.2/ будемо вважати неперервними, диференційованими, а при необхідності – однозначними.

Приклад 1. Циліндрична система координат.

Циліндричними координатами точки М є

Вони зв’язані з декартовими координатами за допомогою відомих співвідношень

Приклад 2. Сферична система координат.

Сферичними координатами точки є

При цьому

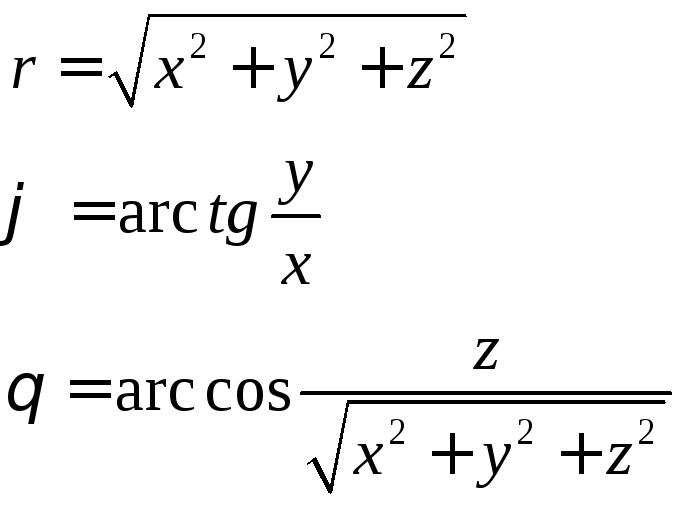
Приклад 3. Криволінійні координати точки задані рівняннм

У першому з рівнянь /28.2/ зафіксуємо криволінійну координатну , тобто приймемо

Очевидно, це є рівнянням певної поверхні в просторі , яку ми будемо називати координатною поверхнею. Існують всього три координатні поверхні.

-93-

Вони перетинаються вздовж трьох ліній

Які ми будемо називати координатними лініями.

Координатні лінії, в свою чергу перетинаються в одній точці М

Означення .Якщо три координатні лінії є взвємно перпендикулярними в кожній точці простору, то криволінійнап систеиа координат називається ортогональною.

Поверхня

Є циліндром радіуса , поверхня

-площиною, яка проходить через вісь і утворює кутз площиноюповерхня

-площина, паралельна до площини на віддалівід цієї

площини. Як видно з рис.73, три лінії є взаємо перпендикулярними.

Подібним чином переконуємось, що ортогональною є і сферична система координат. Координатними поверхнями є

-сфера радіуса

-94-

- площина що проходить через вісь і утворює кутз площиною

- конус, описаний навколо осі , твірна якого утворює кутз віссю. Як видно з рис. 74. три кривіє ортогональними.

Розглянемо криволінійний простір, визначений координатами

тобто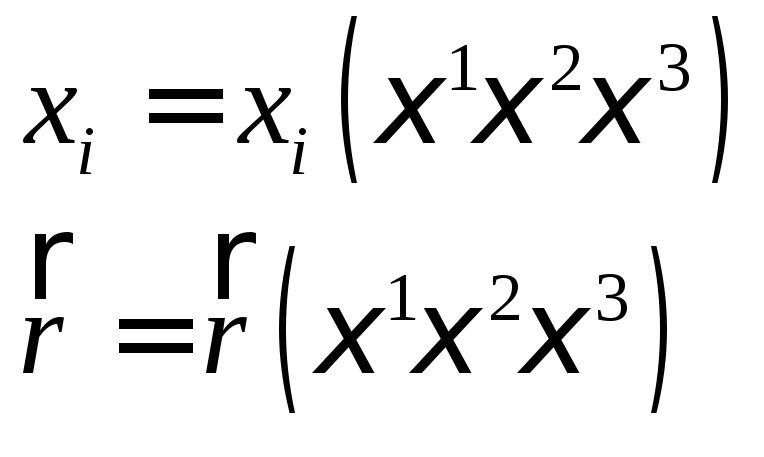

поруч з точкою М, визначеною радіусом-вектором , розглянемо нескінченно близьку точкуз радіусом-вектором. Тоді

/28.4/

порівняємо цей вираз з формулою

І, зокрема з формулою

Де - масштабні вектори косокутної системи,- контраваріантні складові вкктора. У рівності /28.4/ми можемо вважати контраваріантними складовими вектора.

Тоді можна інтегрувати як масштабні вектори в криволінійній системі координат

На відміну від косокутної системи часткові похідні є змінними величинами, тому

-кожній точці криволінійного простору можна поставити у відповідність

-95-

косокутну систему. Визначену масштабними векторами . Таку косокутну систему називають локальною або репером.

Нарисуємо координатні поверхні і координатні лінії, що відповідають точці М криволінійного простору. Нехай точка лежить на координатній лінії, тоді

У нашому конкретному випадку / точка знаходиться на лінії

І тому

-вектори іколінеарні, векторє дотичним до координатної лінії. З другого боку

Де - довжина дуги, тому

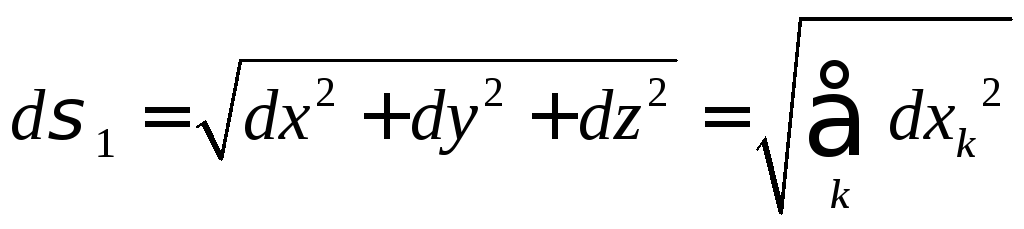
вираз

називають коефіцієнтом Ламе. Враховуючи, що

одержимо

Взагалі: масштабний вектор є дотичним до координатної осі, його довжина дорівнює коефіцієнтові Ламе

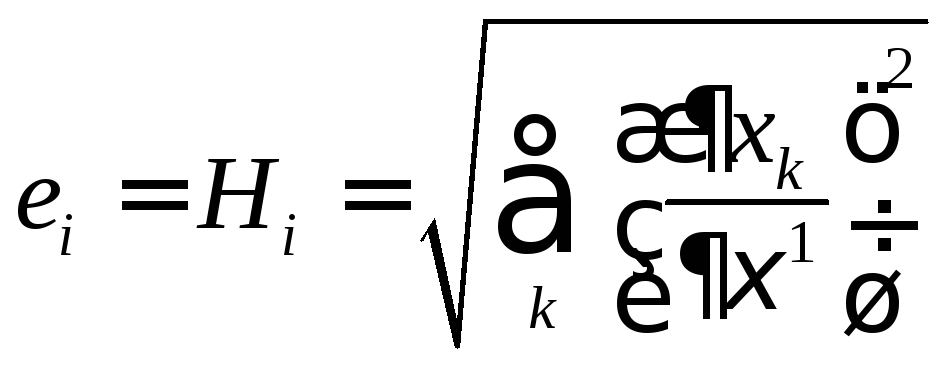
За аналогією з теорії косокутних координат введемо луальні вектори в криволінійному просторі. Будемо виходити з формули

-96-

Приймаючи , ми одержуємо

З другого боку

Порівнюючи дві останні рівності маємо

Легко переконатися, що як і для косокутних координат

дійсно

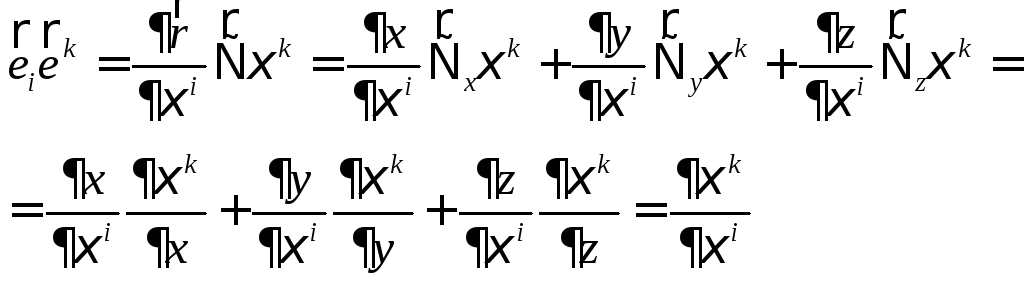
Тому що незалежні координати, похіднаі дорівнює символу Крон екера.

Зауважимо, що вектор - перпендикулярний до поверхні. Це випливає з загальних властивостей градієнта скалярної функції/ див, 6/

29.матричний тензор в криволінійних координатах

Повернемося до формули

І згадаємо. Що величини є контраваріантними складовими векторау локальній системі координат, визначеній масштабними векторами. Коваріантні складові вектора визначається рівністю

Розкриємо скалярний добуток в декартові системі

-97-

І врахуємо, що

Тоді /29.1/

Введемо позначення

/29.2/

Формула /29.1/ визначає операцію опускання індекса у контраваріантного вектора

/29.3/

Отже, величини треба інтерпретувати як коваріантні складові метричного тензора.

Таким чином. Ми ввели коваріантний метричний тензор у криволінійному просторі.легко бачити, що /29.2/ формально збігається з означенням метричного тензора в косокутному просторі

У випадку ортогональної криволінійної системи

Приклад І. знайдемо компоненти метричного тензора для циліндричної системи координат.

Маємо

-98-

.

Приклад 2.Компоненти метричного тензора для сферичної системи координат

, ,,

, ,.

Нескладний підрахунок дає:

,

,

,

,

,

.

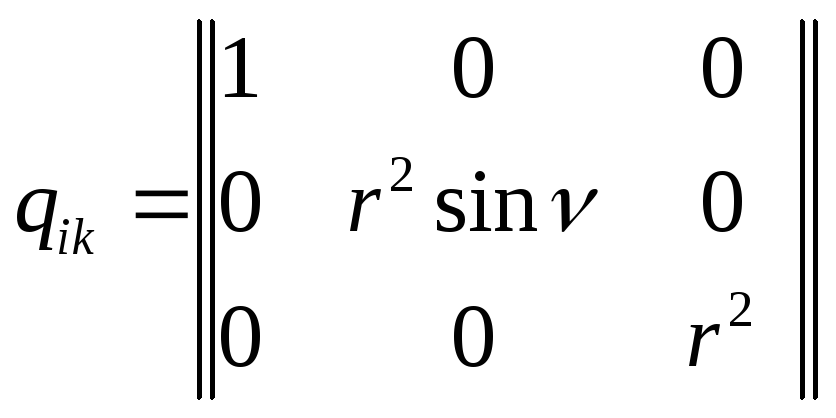Приклад 3. Знайдемо компоненти метричного тензора для координат поверхні тора

Координати поверхні тора пов’язані з декартовими за допомогою таких співвідношень:

,

,

,

Приймаючи

, ,,

маємо

_-99-

,

,

,

,

,

.

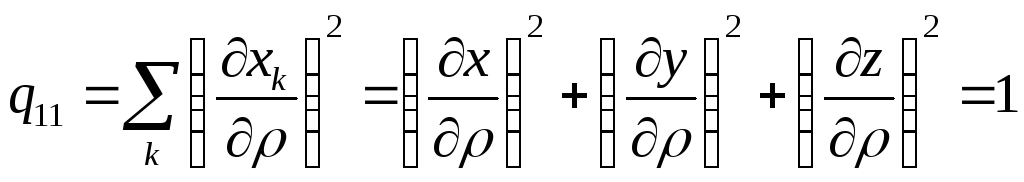Контраваріантні складові метричного тензора визначимо за формулами:

, /29.6/

тобто

. /29.7/

Як і в теорії косокутних координат, коваріантний метричний тензор зв’язаний з контраваріантним відомим співвідношенням:

. /29.8/

Справедливість цієї формули очевидна з такого ланцюга рівностей:

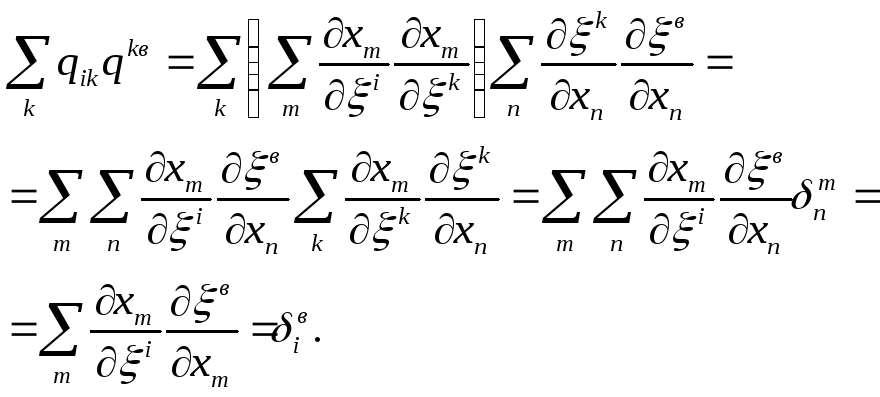
-100-

Зокрема, якщо криволінійна система ортогональна співвідношення між ко- і контраваріантними складовими метричного тензора істотно спрощуються. Наприклад, при

,

,

і взагалі

, .

У випадку ортогональної системи дуальний базис в ортогональним подібно як і базис. Приймаючи в /29.8/маємо

,

, ,,

і взагалі

, .

Приклад 1.Матриця контрваріантного метричного тензора для циліндричної системи координат має вигляд

,

що можна перевірити безпосередньо

,

,

,

-101-

,

,

.

Приклад 2.Для сферичної системи координат

.

Зафіксуємо точку криволінійного простору і розглянемо в цій точці вектор. Його ко- і контраваріантні складові визначені формулами

, ,

.

Перемножуючи останню рівність на , одержимо

,

і аналогічно

.

Таким чином, відомі правила опускання і піднімання індексів справедливі і в криволінійному просторі.

Нехай задане векторне поле .

-102-

Ми можемо говорити про ко- і контраваріантні складові вектора в різних точках простору. При переході від точкидо точкискладові вектора змінюються:

а) за рахунок зміни вектора при переході від однієї точки простору до іншої;

б) за рахунок зміни репера /масштабних векторів /.

Рис. 77

Всі формули теорії косокутних координат залишаються правильними і для криволінійних просторів тільки тоді, коли мова йде про одну і цю ж точку простору.

В розв’язуванні проблем дослідник укріплює свої сили, знаходить нові методи і нові точки зору, відкриває більш широкі і вільні горизонти.

Д.Гільберт