Оглавление

ЗАДАНИЕ 3

РЕФЕРАТ 5

ВВЕДЕНИЕ 6

1 ПОСТАНОВКА ЗАДАЧИ 9

2 ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ 11

ВЫВОДЫ 24

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ 25

ПРИЛОЖЕНИЕ А 26

Задание

на курсовой проект по дисциплине

« Математические методы исследования операций »

Группа ИТ-09-т вариант № 10

Черновой Татьяне Викторовне

Тема проекта:

1. Используя метод штрафных функций, решить задачи нелинейного программирования: найти максимальное и минимальное значения функции z=f(x₁,x₂) при заданных ограничениях на ее переменные.

Условия задачи: z=x+x-10x₁-4x₂

2.Спроектировать контейнер в форме прямой призмы, две грани которой представляют собой равнобочные трапеции, а остальные - прямоугольники (см. рис. 1.1), емкостью V м³ таким образом, чтобы площадь его поверхности имела наименьшее значение.

Рисунок 1.1 – Проектируемый контейнер

Дополнительные условия:

Задание получила: ______________ Т.В. Чернова

(подпись)

Задание выдала: ______________ О.В. Веремей

(подпись)

Дата выдачи 25 сентября 2012 г

Реферат

Курсовой проект по дисциплине «Математические методы исследования операций» на тему: «Методом штрафных функций, решение задачи нелинейного программирования: найти максимальное и минимальное значения функции z=f(x₁,x₂) при заданных ограничениях» и «Проектирование контейнера в форме прямой призмы, две грани которой представляют собой равнобочные трапеции, а остальные - прямоугольники». Студентки группы ИТ-09–т Черновой Татьяны Викторовны. Содержит 38 страниц машинописного текста, 5 рисунков, 1 приложения.

В проекте разработано два программных продукта.

Первый ПП решает задачу нелинейного программирования, методом штрафных функций, находит максимальное и минимальное значение функции.

Второй ПП определяет оптимальные размеры контейнера, методом оптимизации.

Целью данного проекта является освоение методики моделирования и решения задач нелинейного программирования на ЭВМ, а также разработку математической модели объекта и его оптимальное проектирование на ЭВМ различными методами.

ОПТИМИЗАЦИЯ, МАКСИМАЛЬНОЕ И МИИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ, ШТРАФНЫЕ ФУНКЦИИ, КОНТЕЙНЕР

Введение

Оптимизация - модификация системы для улучшения её эффективности. Система может быть одиночной компьютерной программой, набором компьютеров или даже целой сетью, такой как Интернет.

Хотя целью оптимизации является получение оптимальной системы, истинно оптимальная система в процессе оптимизации достигается далеко не всегда. Оптимизированная система обычно является оптимальной только для одной задачи или группы пользователей: где-то может быть важнее уменьшение времени, требуемого программе для выполнения работы, даже ценой потребления большего объёма памяти; в приложениях, где важнее память, могут выбираться более медленные алгоритмы с меньшими запросами к памяти.

Более того, зачастую не существует универсального решения, которое работает хорошо во всех случаях, поэтому инженеры используют компромиссные (англ. tradeoff) решения для оптимизации только ключевых параметров. К тому же, усилия, требуемые для достижения полностью оптимальной программы, которую невозможно дальше улучшить, практически всегда превышают выгоду, которая может быть от этого получена, поэтому, как правило, процесс оптимизации завершается до того, как достигается полная оптимальность. К счастью, в большинстве случае даже при этом достигаются заметные улучшения.

Оптимизация должна проводиться с осторожностью. Тони Хоар впервые произнёс, а Дональд Кнут впоследствии часто повторял известное высказывание: «Преждевременная оптимизация — это корень всех бед». Очень важно иметь для начала озвученный алгоритм и работающий прототип.

В настоящее время оптимизация находит применение в науке, технике и в любой другой области человеческой деятельности. Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку решение задач оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.

Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:

• количество продукции - расход сырья;

• количество продукции - качество продукции.

Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.

При постановке задачи оптимизации необходимо:

• Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Приведем примеры. Типичный пример неправильной постановки задачи оптимизации: «Получить максимальную производительность при минимальной себестоимости». Ошибка заключается в том, что ставится задача поиска оптимальности 2-х величин, противоречащих друг другу по своей сути. Правильная постановка задачи могла быть следующая: а) получить максимальную производительность при заданной себестоимости; б) получить минимальную себестоимость при заданной производительности; В первом случае критерий оптимизации - производительность а во втором - себестоимость.

• Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта.

• Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.

• Учет ограничений.

Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант работы объекта должен оцениваться какой-то количественной мерой - критерием оптимальности. Критерием оптимальности называется количественная оценка оптимизируемого качества объекта. На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации. Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

В зависимости от своей постановки, решение оптимизационных задач может производиться различными методами, и наоборот – любой метод может применяться для решения многих задач. Методы оптимизации могут быть скалярными (оптимизация проводится по одному критерию), векторными (оптимизация проводится по многим критериям), поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.), вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.), теоретико-вероятностными, теоретико-игровыми и др. Подвергаться оптимизации могут задачи как с ограничениями, так и без них.

1 Постановка задачи

1.1 Задание 1 «Оптимизация нахождения максимума и минимума»

Для нахождения максимального и минимального значение функции ,необходимо:

1. построить область допустимых значений, определяемую ограничениями задачи.

2. определить тип поверхности и линии уровня описываемой целевой функции.

3. составить штрафную и вспомогательную целевую функцию.

4. определить исходную точку из которой будет начало движения к экстремуму.

5. выбрать метод оптимизации, а затем получаем глобальный минимум и максимум.

Задача оптимизации состоит в том чтобы найти максимум и минимум функции: z=x+x-10x₁-4x₂.

1.2 Задание 2 «Оптимизация размера контейнера»

Предприятие занимается перевозкой грузов – контейнера, средством перевозки является самолет. Оптимизация контейнера производится под размеры рампы (грузолюка).

Проектируем контейнер, который нужно поставить в грузовой отсек, таким образом, чтобы он был соответствующего размера. Если контейнер будет больше нужного размера, то он не поместится в отсек для груза. Если контейнер будет меньшим нужного размера, то он будет лежать неустойчиво, что может привести к повреждениям груза. Таким образом, нам нужно рассчитать нужный размер контейнера для перевозки.

Поверхность контейнера должна быть без нижней грани, рисунка 1.

1.3 Ограничения задачи

Задание 1.

Ограничения для задачи нахождения минимума и максимума функции выглядит таким образом:

Задание 2.

Ограничения для контейнера:

Объем контейнера V = 2.

Ограничения на размеры L  2.8; c/b =2. Поверхность контейнера должна быть без правой стенки, рисунка 1.

2 Описание предметной области

2.1 Математическая модель

2.1.1 Расчет штрафной и вспомогательной целевой функции

Преобразуем исходную систему ограничений в каноническую форму задачи нелинейного программирования :

8-х1-2х2>=0

3-х2>=0

x1,x2>=0

Формула штрафной функции:

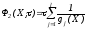
где t - некоторый параметр, l – количество неравенств ограничений, g_j – левая часть неравенства ограничения.

Полученная вспомогательная целевая функция:

F₁(X,t) = Z(X) + Ф2(X,t), где X=(x₁,x₂), Z(X) = x+x-10x₁-4x₂

Поиск максимума функции f сводится к поиску минимума функции

F₂(X,t) = -Z(X) + Ф2(X,t).

Использование метода внутренних штрафных функций (метода внутренней точки) позволяет удерживать траекторию поиска внутри допустимой области. Метод применяется для решения задач минимизаци с ограничениями-неравенствами, то есть

D_X={X/g_j(X)0, j=}.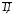

Кроме того, при его использовании начальная точка X₀ должна принадлежать середине области D_X, то есть X₀D_X, X₀dD_X.

Функция штрафа .

С приближением X к границе области D_X (см. рис. 2.1) значение Ф₁ растёт к бесконечности. Это явление вызвано наличием непреодолимого барьеру на границе области

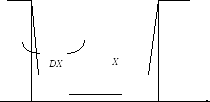
Рисунок 2.1 - Приближением X к границе области D_X

_ъ

При использовании функции Ф₂ решают последовательность задач безусловной оптимизации функции F(X,) с значениями , что монотонно уменьшаются на каждом этапе.

2.1.2 Расчет целевой функции и ограничений

Определим площадь поверхности призмы:

где - площадь поверхности призмы;-длины сторон оснований призмы;-высота призмы;-длина бокового ребра призмы.

Объем призмы рассчитывается по формуле:

где 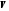-объем призмы.

Стороны верхнего и нижнего оснований призмы находятся в зависимости:

Длину бокового ребра можно определить по формуле:

Объединяя формулы (1)..(4) получим площадь поверхности , зависящую от двух параметрови:

Для того, чтобы решить поставленную задачу методами оптимизации, воспользуемся методом внешних штрафных функций. Для этого составим вспомогательную функцию , имеющую вид:

где -вспомогательная функция;-целевая функция;-вектор,,-матрица ограничений,,-коэффициент штрафа.

Матрица ограничений имеет вид:

Поставленную задачу решаем методом Фиако – МакКормика с использованием метода внешних функций.

2.1.3 Расчет системы уравнений

Для удобства дифференцирования функции , перепишем ее в виде:

Найдем частные производные функции функции по независимым переменным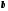и

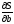Для того, чтобы площадь поверхности призмы была минимальна, необходимо, чтобы были равны нулю частные производные и. Получим систему двух нелинейных уравнений:

2.2 Описание методов используемых в заданиях

2.2.1 Описание метод внешних штрафных функций

В методах внешних штрафных функций (методах внешней точки) функциями штрафа для ограничений типа могут быть выбраны

При использовании этих функций не нужно, чтобы начальная точка X₀ принадлежала допустимому участку D_X. Функции ведут себя следующим образом (см. рис. 2.2):

С уменьшением  (ростом 1/) будут сближаться условный минимум f(X) и безусловный минимум F(X,). При 0 эти минимума сливаются.

Следует заметить, что если условный минимум функции f(X) лежит внутри участка D_X, то он одновременно есть и безусловным, так как для XD_X всегда min[g_j(X),0]=0[3],[4].

2.2.2 Описание метода наискорейшего спуска

Использование метода внутренних штрафных функций (метода внутренней точки) позволяет удерживать траекторию поиска внутри допустимой области. Метод применяется для решения задач минимизаци с ограничениями-неравенствами, то есть

D_X={X/g_j(X)0, j=}.

Кроме того, при его использовании начальная точка X₀ должна принадлежать середине области D_X, то есть X₀D_X, X₀dD_X.

Функция штрафа .

С приближением X к границе области D_X значение (см. рис. 2.3) Ф₁ растёт к бесконечности. Это явление вызвано наличием непреодолимого барьеру на границе области

Рисунок 2.3 - Приближением X к границе области D_X

При использовании функции Ф₂ решают последовательность задач безусловной оптимизации функции F(X,) с значениями , что монотонно уменьшаются на каждом этапе[5].

2.2.3 Описание метода Морринсона

Метод применяется для задач нелинейного программирования с ограничениями вида неравенств, то есть подходит для данной задачи. Метод аналогичен методу штрафных функций. Для минимизации функции f(X) при заданных ограничениях вида g_j(X)  0, j=1..m, где m – количество ограничений. Вводится вспомогательная функция:

.

Итерационная формула:

, где иX_k определяются из условия минимизации

.

Начальную точку можно выбирать произвольно, но желательно внутри заданной области ограничений. Параметр ₀ следует выбрать так, чтобы ₀F(X*), а т.к. F(X*)=f(X*), то ₀ заранее неизвестно. В нашей задаче известно, что f(X*) положительна, поэтому примем ₀=0.

Условия окончания вычислительного процесса:

1) ||X_k – X_k+1|| <e;

2) f(X_k)- _k<e(1 + |_k|);

3) _k+1 - _k<e(1 + |_k|).

После окончания вычислений X* = X_k+1; f* = f(X*).

2.3 Алгоритмы методов

2.3.1 Алгоритм метода штрафных функций

1. Строим штрафную функцию и выбираем начальную точку и произвольный коэффициент штрафа.

2. С помощью любого метода безусловной оптимизации находим экстремум функции x¹(r¹). Начиная с точки x¹(r¹) с помощью метода безусловной оптимизации ищем экстремум функции U(x,r²), где r¹>r²>0.

3. Описанную процедуру продолжаем до тех пор, пока |U(x,r^k+1)-U(x,r^k)|<eps.

2.3.2 Алгоритм метода оптимизации(наискорейшего спуска)

1. Выбор начальной точки X₀ (произвольно).

2. Полагаем k = 1. Начальное значение t = 1.

3. Методом наискорейшего спуска находим минимум функции F(X,t), получаем точку (X_k,t_k)..

4. Проверка условия окончания поиска:||X_k – X_k-1|| <e или ||f(X_k) – f(_k-1)|| <e.

5. Уменьшение t: t = t/R, где R=5..10.

6. k = k + 1, переход на этап 3.

7. X^* = X_k; f^* = f(X^*).

2.3.3 Алгоритм метода Морринсона

1. Выбор начальной точки X₀ (произвольно).

2. Полагаем k = 1. Начальное значение _k = 0.

3. Методом наискорейшего спуска находим минимум функции F(X, _k), получаем точку (X_k, _k). Вычисляем F(X_k, _k)

4. Проверка условия окончания поиска:

||X_k – X_k-1|| <e или f(X_k)- _k<e(1 + |_k|). Если условие выполняется, переход на этап 7.

5. Изменение _k: .

6. k = k + 1, переход на этап 3.

7. X^* = X_k; f^* = f(X^*).

3 РАЗРАБОТКА ПРОГРАММНОГО ПРОДУКТА

3.1 Выбор средств реализации

Данный программный продукт разработан в среде программирования Delphi 7 под Windows.

Delphi – общепризнанный лидер среди инструментов для создания приложений и систем, функционирующих на платформе Windows. Передовая объектно-ориентированная технология визуального проектирования позволяет отдельным программистам и коллективам разработчиков почувствовать уверенность в возможности полного удовлетворения запросов самых требовательных пользователей и устойчивость своего положения на рынке высоких технологий.

Сочетание возможностей быстрого прототипирования приложений с технологиями уровня предприятия обеспечивает плавное и предсказуемое развитие проектов любого масштаба. Следование стандартам индустрии и открытость к взаимодействию с любыми частными решениями гарантирует успех проектов, разрабатываемых с использованием Delphi.

В библиотеки визуальных компонентов Delphi включено множество типов компонентов, и их номенклатура очень быстро расширяется от версии к версии.

Delphi базируется на языке Object Pascal. Компиляторы с языков семейства Паскаль фирмы Borland были одними из самых быстрых компиляторов. В настоящее время Object Pascal – это объектно-ориентированный язык с твердой опорой в виде хорошего компилятора.

В настоящее время приложения, как правило, должны функционировать не сами по себе, а являться частью некоторой информационной системы. В этом случае один из основных вопросов – организация взаимного общения приложений друг с другом и с базами данных. Приложения Delphi имеют доступ к ряду современных технологий, разработанных на основе спецификаций OLE,COM,DCOM.

Delphi 7 имеет уникальную особенность: она способна создавать так называемые межплатформенные приложения, т.е. программы, которые одинаково успешно могут работать как под управлением Windows 32, так и под Linux.

В основе поддержки распределенных вычислений в Delphi лежит два важнейших принципа: ориентация на стандарты и высокоуровневая разработка клиентской и серверной логики приложений на основе компонентной модели. Комплекс технологий, компонентов, инструментов и средств поддержки объектных инфраструктур (middleware): COM, CORBA, XML – MIDAS – является неотъемлемой частью Delphi 7.

Delphi, как мощная система визуального объектно-ориентированного программирования позволяет решать множество задач, в частности:

• создавать законченные приложения для Windows самой различной направленности, от вычислительных и логических, до графических и мультимедиа;

• быстро создавать профессионально выглядящий интерфейс для любых приложений, написанных на любом языке;

• создавать мощные системы работы с локальными базами данных любых типов;

• создавать многозвенные распределенные приложения, основанные на различных технологиях;

• создавать приложения, которые управляют другими приложениями;

• и многое другое, включая создание отчетов, справочных систем, библиотек DLL.

В целом Delphi – великолепный инструмент, как для начинающих программистов, так и для ассов программирования [6].

3.2 Требования к аппаратным средствам

Для эффективной работы программного продукта необходимо выполнение следующих требований к аппаратному и программному обеспечению:

1. ОС: Windows 98/Me/NT/2000/XP/Vista

2. процессор: 1 Ггц

3. память: система требует минимум 256 Мб оперативной памяти.

4. управление: требуется клавиатура и мышь

5. устройства чтения: 1 Гб свободного места на жестком диске для установки и запуска системы

6. Borland Delphi 7

3.3 Порядок работы с программой

Задание 1.

При запуске программы появляется окно главной формы показано на рисунке 3.1. Задаем начальные точки, нажимаем кнопку «Расчет». Просматриваем результаты.

Рисунок 3.1 – Окно главной формы

Задание 2.

При запуске программы появляется окно главной формы показано на рисунке 3.2. Выбираем способ решения, нажимаем кнопку «Вычисление». Просматриваем результаты.

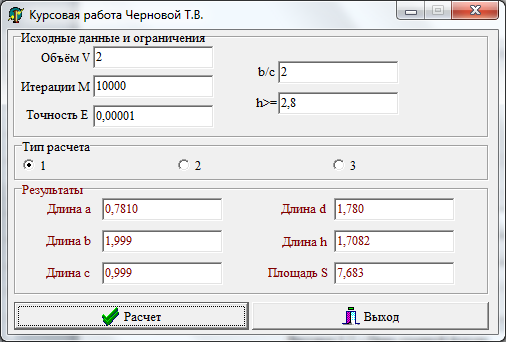
Рисунок 3.2 – Окно главной формы

3.4 Результаты работы программ

1 задание

В результате проведенной работы было установлено, что метод штрафных функций обеспечивает точность, достаточную для поставленной задачи.

Max: x1=0; x2=1,59999; f=-0,003999;

Min: x1=4,8000; x2=0,001 f=-28,8.

2 задание

В результате проведенной работы было установлено, что метод штрафных функций обеспечивает точность, достаточную для поставленной задачи.

Результат расчета с использованием второго ограничения на размеры и методов дифференциального исчисления:

• первый способ – непосредственное нахождение минимума функции f(c,h):

a = 0,7810; b = 0,999; c = 1,999; d = 1,780; h = 1,7082; S = 7,683;

• второй способ – решение системы уравнений:

a = 0,7810; b = 0,999; c = 1,999; d = 1,780; h = 1,7082; S = 7,683;

• третий способ – используется ограничение на d:

a = 0,6003; b = 0,793; c = 1,587; d = 2,828; h = 2,7997; S = 8,155;

Заметим, что решения задачи первым и вторым способами мало отличаются друг от друга. Это свидетельствует о правильности решения.

ВЫВОДЫ

Задание 1. В результате проведенной работы было установлено, что метод штрафных функций обеспечивает точность, достаточную для поставленной задачи. На количество итераций больше всего влияет начальное значение t и точность e. Для расчетов на минимум принято t₀=1; на максимум – t₀=0.001.

Задание 2. В ходе решения задачи проектирования контейнера были установлены следующие оптимальные размеры а=1,27087м; b=0,31478м; c=0,94435м; d=2,51944м; h=2,4997м; S=7,94953м2 для перевозки 1-м и 2-м методами, это свидетельствует о правильном решении задачи.

Результат в 3-м методе отличается от результатов в 2-х предыдущих методах – это обусловлено различием в ограничениях в первых двух и 3-м методах.

Перечень используемых источников

1. Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высш. шк., 1986. - 319 с.

2. Мину М. Математическое программирование. - М.: Наука, 1990.-- 488 с.

3. Ю.П. Зайченко. Исследование операций: нечеткая оптимизация. Киев, Выща школа, 1991.- 192с.

4. Пантелеев А.В. и др. Методы оптимизации в примерах и задачах: Учеб. пособие – М.: Высш. шк.., 2002. – 544 с.: ил.

5. Программирование в среде Delphi: Лабораторный практикум для студентов всех специальностей. Под общей редакцией Синицына А.К. – Мн.; БГУИР, 1998. – 94 с.

6. Архангельский А.Я. Программирование в Delphi 6 ––М.: ЗАО «Издательство БИНОМ», 2002г. – 1200 с.

7. Программирование в среде Delphi: Лабораторный практикум для студентов всех специальностей. Под общей редакцией Синицына А.К. – Мн.; БГУИР, 1998. – 94 с.

Приложение а

1. Листинг программы к задачи нахождения минимума и максимума функции:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls, TeeProcs, TeEngine, Chart, Series, ArrowCha;

type

TForm1 = class(TForm)

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Edit4: TEdit;

Edit5: TEdit;

Edit6: TEdit;

Edit7: TEdit;

Edit8: TEdit;

Button1: TButton;

Memo1: TMemo;

Memo2: TMemo;

Chart1: TChart;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Label6: TLabel;

Label7: TLabel;

Label8: TLabel;

Label9: TLabel;

Label10: TLabel;

Label11: TLabel;

Label12: TLabel;

Series1: TArrowSeries;

Series2: TArrowSeries;

Series3: TArrowSeries;

Series4: TArrowSeries;

Label13: TLabel;

Label14: TLabel;

Label15: TLabel;

Edit9: TEdit;

Edit10: TEdit;

procedure Button1Click(Sender: TObject);

procedure DrawLines;

PROCEDURE OPGRAD(N:INTEGER;E:REAL);

private

{ Private declarations }

public

{ Public declarations }

end;

const n=2; kol=8; zmin=0.2;

nmax=100;e=0.000001;

Graph1Color = clBlue;

Graph2Color = clRed;

BorderColor = clBlack;

LineColor = clGreen;

R = 5;

type mas=array [1..n] of real;

artype=array[1..n] of real;

function f(x:mas):real;

function poisk(x:mas;h,t:real;typ:integer):mas;

function eq(x1,x2:mas):boolean;

procedure m1(x:mas;h,t,eps:real;MaxIt,typ:integer);

function shtf(x:mas;T:real):real;

function fgran(x:mas;i:byte):mas;

function gr(x:mas;i:byte):real;

var

Form1: TForm1;

T:real;

G,X,Xk:mas;

fopt:real;

nn:integer;

xm,ym:real;

lambda:real;

s:real;

implementation

{$R *.dfm}

function fgran(x:mas;i:byte):mas;

begin

fgran:=x;

case i of

1:fgran[2]:=(6-2*x[1])/3;

2:fgran[2]:=(3*x[1]-18)/2;

3:fgran[2]:=(x[1]+8)/2;

4:fgran[1]:=0;

5:fgran[2]:=0;

end;

end;

function gr(x:mas;i:byte):real;

var r:real;

begin

case i of

1: r:=8-X[1] - 2*X[2];

2: r:=-X[2] + 3;

3: r:=x[1];

4: r:=x[2];

end;

result:=r;

end;

function gf(x:mas):real;

var i:integer;

r:real;

begin

r:=0;

for i:=1 to 5 do

begin

if gr(x,i)<0 then begin r:=1e10; break; end;

if gr(x,i)=0 then begin r:=1e5; break; end;

r:=r+1/gr(x,i);

end;

result:=r;

end;

function f(x:mas):real;

begin

f:=sqr(x[1])+sqr(x[2])-10*x[1]-4*x[2];

end;

function shtf(x:mas;T:real):real;

begin

shtf:=f(x)+T*GF(x);

end;

function poisk(x:mas;h,t:real;typ:integer):mas;

var x1,x2,minx:mas;

i,j,k:integer;

begin

result:=x;

minx:=x;

for i:=1 to n do

begin

x1:=x;x2:=x;

x1[i]:=x[i]+h;

x2[i]:=x[i]-h;

for j:=1 to 5 do

begin

if (gr(minx,j)<1e-3) or (gr(x2,j)<1e-3) or (gr(x1,j)<1e-3) then

begin

x1:=fgran(x1,j);

x2:=fgran(x2,j);

for k:=1 to 5 do

if (j<>k) and ((gr(x2,k)<1e-3) or (gr(x1,k)<1e-3)) then exit;

if typ=0 then

begin

if f(x1)<f(x2) then minx:=x1 else minx:=x2;

if f(minx)>f(x) then minx:=x

else result:=minx;

end

else

begin

if f(x1)>f(x2) then minx:=x1 else minx:=x2;

if f(minx)<f(x) then minx:=x

else result:=minx;

end

end;

end;

if not ((result[1]=x[1]) and (result[2]=x[2])) then exit;

if typ=0 then

begin

if shtf(x1,t)<shtf(x2,t) then minx[i]:=x1[i] else minx[i]:=x2[i];

if shtf(minx,t)>shtf(x,t) then minx[i]:=x[i];

end

else

begin

t:=-abs(t);

if shtf(x1,t)>shtf(x2,t) then minx[i]:=x1[i] else minx[i]:=x2[i];

if shtf(minx,t)<shtf(x,t) then minx[i]:=x[i];

end;

end;

if ((typ=0) and (shtf(minx,t)>shtf(x,t)))

or ((typ=1) and (shtf(minx,t)<shtf(x,t))) then minx:=x;

result:=minx;

end;

function eq(x1,x2:mas):boolean;

var i:integer;

begin

eq:=true;

for i:=1 to n do

if x1[i]<>x2[i] then

begin

eq:=false;

break;

end;

end;

procedure m1(x:mas;h,t,eps:real;maxIt,typ:integer);

var k,i:integer;

min:real;

x1:mas;

qq:mas;

begin

qq[1]:=2;

qq[2]:=3;

for i:=1 to 5 do

if gr(x,i)<=0 then

begin

showmessage('Выбранная начальная точка находится'+#13+'вне внутренней области!');

exit;

end;

min:=f(x);k:=0;

while (t>=0)and (k<=maxIt)do

begin

x1:=poisk(x,h,t,typ);

if (eq(x,x1)) then begin h:=h/2; end;

k:=k+1;

if typ=0 then begin

if (k>1) and (x[1]<>x1[1]) and (x[2]<>x1[2]) then begin

form1.Memo1.Lines.Add(' x1='+copy(floattostr(x[1]),1,5)+' x2='+copy(floattostr(x[2]),1,5)

+' f='+floattostr(f(x1))) ;

end; end

else begin

if (k>1) and (x[1]<>x1[1]) and (x[2]<>x1[2]) then begin

form1.Memo2.Lines.Add(' x1='+copy(floattostr(x[1]),1,5)+' x2='+copy(floattostr(x[2]),1,5)

+' f='+floattostr(f(x1))) ;

end;

end;

x:=x1;

T:=T/2;

end;

if typ=0 then begin

form1.Edit3.Text:=floattostr(x[1]);

form1.Edit4.Text:=floattostr(x[2]);

form1.Edit5.Text:=floattostr(f(x1));

form1.Series1.AddArrow(qq[1],qq[2],X[1],X[2],'',clblue);

end

else begin

form1.Edit7.Text:=floattostr(x[1]);

form1.Edit8.Text:=floattostr(x[2]);

form1.Edit6.Text:=floattostr(f(x1));

form1.Series2.AddArrow(qq[1],qq[2],X[1],X[2],'',clred);

end;

end;

procedure TForm1.Button1Click(Sender: TObject);

var x:mas;

eps,h:real;

mi:integer;

begin

Memo1.Clear;

Memo2.Clear;

Series1.Clear;

Series2.Clear;

Series3.Clear;

Series4.Clear;

Series3.AddArrow(0,4,10,9,'',BorderColor);

Series3.AddArrow(10,9,6,0,'',BorderColor);

Series3.AddArrow(6,0,3,0,'',BorderColor);

Series3.AddArrow(3,0,0,2,'',BorderColor);

Series3.AddArrow(0,2,0,4,'',BorderColor);

DrawLines;

x[1]:=strtofloat(Edit1.Text);

x[2]:=strtofloat(Edit2.Text);

h:=0.2;

T:=1;

eps:=0.0001;

mi:=10000;

m1(x,h,t,eps,mi,0);

m1(x,h,t,eps,mi,1);

Label14.Caption:='X1=2';

Label15.Caption:='X2=2';

opgrad(2,e);

end;

procedure TForm1.DrawLines;

const N = 100;

FMIN = -10;

FMAX = 30;

Del = 6;

Dang = 2*pi/N;

Xc =4;

Yc =2;

var ang,r,f,x,y,x2,y2 : real;

c : TColor;

rr,g,b : byte;

begin

{Только для заданной функции!!!}

form1.Series4.Clear;

f := FMIN + Del;

c := clBlack;

r := 0;

g := 0;

b := 0;

While f <= FMAX do begin

r := sqrt((f - FMIN)/1);

f := f + Del;

ang := 0*pi/180;

x := Xc + r*cos(ang);

y := Yc + r*sin(ang);

ang := ang + Dang;

x2 := Xc + r*cos(ang);

y2 := Yc + r*sin(ang);

c := RGB(rr,g,b);

rr := rr + 10;

g := g + 30;

b := b + 50;

form1.Series4.AddArrow(x,y,x2,y2,''{Format('%5.2g',[f])},c);

while ang < 360*pi/180 do begin

x := Xc + r*cos(ang);

y := Yc + r*sin(ang);

ang := ang + Dang;

x2 := Xc + r*cos(ang);

y2 := Yc + r*sin(ang);

form1.Series4.AddArrow(x,y,x2,y2,'',C);

end;

end;

end;

PROCEDURE GRAD(N:INTEGER;E:REAL;X:mas);

VAR I:INTEGER; FP,FO :REAL;

BEGIN

FOR I:=1 TO N DO BEGIN

X[I]:=X[I]+E; FP:=F(X);

X[I]:=X[I]-2*E; FO:=F(X);

X[I]:=X[I]+E; G[I]:=(FP-FO)/2/E;

END;

END;

PROCEDURE Tform1.OPGRAD(N:INTEGER;E:REAL);

LABEL 1;

VAR DK : ARTYPE; OD,LAMBDA,S,SF : REAL;

I: INTEGER; C: CHAR;

FUNCTION FF(X:REAL):REAL;

VAR I:INTEGER;

BEGIN

FOR I:=1 TO N DO XK[I]:=XK[I]+ABS(X)*DK[I]/OD;

FF:=F(XK);

FOR I:=1 TO N DO XK[I]:=XK[I]-ABS(X)*DK[I]/OD;

END;

PROCEDURE MIN(A,B,E:REAL);

LABEL 1,2;

VAR X,Y,XO,XK,x1,x2,y1,y2:REAL;

BEGIN

XO:=A;XK:=B;

x1:=a+0.382*(b-a);

x2:=b-0.382*(b-a);

y1:=ff(x1);y2:=ff(x2);

1:

if (y1<=y2) then begin b:=x2;

if ((b-a)<e) then goto 2 else

begin

x2:=x1;

x1:=a+0.382*(b-a);

y2:=y1;y1:=ff(x1);

goto 1;

end;

end

else begin a:=x1;

if ((b-a)<e) then goto 2 else

begin

x1:=x2;

x2:=b-0.382*(b-a);

y1:=y2;y2:=ff(x2);

goto 1;

end;

end;

2: xm:=(a+b)/2;

ym:=ff(xm);

END;

BEGIN

NN:=0; LAMBDA:=0;

REPEAT

GRAD(N,E/2,XK);

for i:=1 to n do Dk[i]:=G[i];

FOR I:=1 TO N DO DK[I]:=-DK[I]; SF:=F(XK);

OD:=0;

FOR I:=1 TO N DO OD:=OD+SQR((DK[I]));

OD:=SQRT(OD); IF OD<E THEN GOTO 1;

NN:=NN+1;

IF NN>NMAX THEN BEGIN NN:=NN-1;

FOPT:=F(XK);{ EXIT} END ;

MIN(0,10,E);

LAMBDA:=Xm;

S:=Ym;

FOR I:=1 TO N DO XK[I]:=XK[I]+LAMBDA*DK[I]/OD;

UNTIL (LAMBDA<E) ;

1: FOPT:=F(XK);

form1.Edit9.Text:=floattostr(xk[1]);

form1.Edit10.Text:=floattostr(xk[2]);

END;

end.

2. Листинг программы к задаче для проектирования контейнера:

unit untMain;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

untMeth, StdCtrls, ExtCtrls, Buttons;

type

TfrmMain = class(TForm)

gbxData: TGroupBox;

edtV: TEdit;

lblV: TLabel;

edtE: TEdit;

edtM: TEdit;

lblE: TLabel;

lblM: TLabel;

gbxResult: TGroupBox;

lblA: TLabel;

lblB: TLabel;

lblC: TLabel;

lblD: TLabel;

lblH: TLabel;

lblS: TLabel;

rgpNumber: TRadioGroup;

edtA: TEdit;

edtB: TEdit;

edtC: TEdit;

edtD: TEdit;

edtH: TEdit;

edtS: TEdit;

edtT: TEdit;

edtP: TEdit;

lblT: TLabel;

lblP: TLabel;

BitBtn1: TBitBtn;

BitBtn2: TBitBtn;

procedure BitBtn1Click(Sender: TObject);

procedure BitBtn2Click(Sender: TObject);

end;

var

frmMain: TfrmMain;

v, t, s, e, p: extended;

i, m: integer;

x: TVekt;

implementation

function c(x: TVekt): extended;

begin

c:=x[0];

end;

function h(x: TVekt): extended;

begin

h:=x[1];

end;

function a(x: TVekt): extended;

begin

a:=2*v/(h(x)*c(x)*(t+1));

end;

function b(x: TVekt): extended;

begin

b:=t*c(x);

end;

function d(x: TVekt): extended;

begin

Result:=sqrt(sqr(h(x))+sqr(c(x)*(t-1))/4);

end;

function f(x: TVekt): extended;

var k: extended;

begin

k:=(b(x)+c(x))*(a(x)+h(x))+a(x)*sqrt(4*sqr(h(x))+sqr(b(x)-c(x)));

k:=k-((c(x)+b(x))*h(x)/2);

Result:=k;

end;

function dfc(x: TVekt): extended;

var p: array [1..6] of extended;

begin

p[1]:=h(x)*(t+1)/2;

p[2]:=h(x)*(t+1)/2;

p[3]:=0;

p[4]:=0;

p[5]:=-4*v/(sqrt(4/sqr(c(x))+sqr(t-1)/sqr(h(x)))*(t+1)*c(x)*c(x)*c(x));

p[6]:=-4*v/(sqrt(4/sqr(c(x))+sqr(t-1)/sqr(h(x)))*(t+1)*c(x)*c(x)*c(x));

Result:=p[2]+p[3]+p[4]+p[5]+p[6];

end;

function dfh(x: TVekt): extended;

var p: array [1..6] of extended;

begin

p[1]:=c(x)*(t+1)/2;

p[2]:=c(x)*(t+1)/2;

p[3]:=-2*v*t/sqr(h(x))/(t+1);

p[4]:=-2*v/sqr(h(x))/(t+1);

p[5]:=-v*sqr(t-1)/(sqrt(4/sqr(c(x))+sqr(t-1)/sqr(h(x)))*h(x)*h(x)*h(x)*(t+1));

p[6]:=-v*sqr(t-1)/(sqrt(4/sqr(c(x))+sqr(t-1)/sqr(h(x)))*h(x)*h(x)*h(x)*(t+1));

Result:=p[2]+p[3]+p[4]+p[5]+p[6];

end;

function df(x: TVekt): extended;

begin

df:=sqr(dfc(x))+sqr(dfh(x));

end;

function oh(x: TVekt): extended;

begin

oh:=p-h(x)

end;

function oc(x: TVekt): extended;

begin

oc:=-c(x);

end;

function sf(x: TVekt): extended;

begin

sf:=1000*(sqr((oh(x)+abs(oh(x)))/2)+sqr((oc(x)+abs(oc(x)))/2))

end;

function rf(x: TVekt): extended;

begin

rf:=f(x)+sf(x);

end;

{$R *.DFM}

procedure TfrmMain.BitBtn1Click(Sender: TObject);

begin

Close();

end;

procedure TfrmMain.BitBtn2Click(Sender: TObject);

begin

v := StrToFloat(edtV.Text);

m := StrToInt(edtM.Text);

e := StrToFloat(edtE.Text);

t := StrToFloat(edtT.Text);

p := StrToFloat(edtP.Text);

if t > 1 then t:=1/t;

SetLength(x, 2);

x[0]:=0.0001;

x[1]:=0.0001;

case rgpNumber.ItemIndex of

0: gradmin(f, m, e, x, s, i);

1: begin

gradmin(df, m, e, x, s, i);

s:=f(x);

end;

2: begin

gradmin(rf, m, e, x, s, i);

s:=f(x);

end;

end;

if i = 0 then ShowMessage('Превышено число шагов');

edtA.Text := FormatFloat('0.0000', a(x));

if StrToFloat(edtT.Text) < 1 then

begin

edtB.Text := FormatFloat('0.000', b(x));

edtC.Text := FormatFloat('0.000', c(x));

end

else

begin

edtB.Text := FormatFloat('0.000', c(x));

edtC.Text := FormatFloat('0.000', b(x));

end;

edtD.Text := FormatFloat('0.000', d(x));

edtH.Text := FormatFloat('0.0000', h(x));

edtS.Text := FormatFloat('0.000', s);

end;

end.
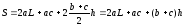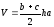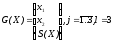
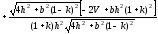