3.3.3 Электрический расчет
Расчет выполняют обычно для горячего режима и нормального заполнения тигля, когда весь металл находится в расплавленном состоянии [10].
Глубина проникновения тока в металл индуктора
,
(3.24)
где ρ1 – удельное сопротивление меди, из которой изготовлен индуктор.
= 0,01 м
Удельное сопротивление меди в пределах 20…1500С меняется линейно от 1,68*10-8 до 2,75*10-8. В расчете температуру меди принимаем равной 60…700С.
Глубина проникновения тока в материал загрузки
,
(3.25)
где ρ2 – удельное сопротивление загрузки; ρ2=0,810-6 Ом*м;
μZ2 –
относительная магнитная проницаемость
загрузки, μZ2=1
.
= 0,06 м
Относительный радиус загрузки (характерный поперечный размер)
.
(3.26)
= 10,8 м
Активное сопротивление индуктора при условии, что толщина внутренней стенки трубки индуктора b1>Δ1. Принимаем толщину трубки 0,05 м.
,
(3.27)
где k3 – коэффициент заполнения индуктора, k3 = 0,82.
= 0,01 · 10-3 Ом.
Активное сопротивление загрузки
,
(3.28)
где А – вспомогательная функция, А = 0,15.
= 0,23 · 10-3 Ом.
Внутреннее реактивное сопротивление индуктора
x1b=r1tgφ, (3.29)
где φ – сдвиг фаз между напряженностями электрического и магнитного полей в металле индуктора. При b1 > 1,5Δ1 tgφ = 1.
x1b = 0,01 · 10-3 Ом·м.
С учетом принятого b = 0,05 м x1 = 0,2 · 10-3 Ом. Внутреннее реактивное сопротивление загрузки
,
(3.30)
где
В = f (R2)
– вспомогательная функция, В = А.
= 0,23 · 10-3 Ом.
Реактивное сопротивление рассеивания
,
(3.31)
где ω – круговая частота тока, ω=2πf, рад/с.
Подставляем данные в формулу (3.31)
= 0,03 · 10-3 Ом.
Реактивное сопротивление пустого индуктора
,
(3.32)
где К – поправочный коэффициент, К = 0,9.
= 0,09 · 10-3 Ом.
Реактивное сопротивление обратного замыкания
.
(3.33)
= 0,91 · 10-3 Ом.
Коэффициент приведения параметров загрузки к цепи индуктора
.
(3.34)
= 0,84
Приведенное активное сопротивление загрузки
r2’ = c · r2. (3.35)
r2’ = 0,84 · 0,23 · 10-3 = 0,18 · 10-3 Ом.
Приведенное реактивное сопротивление загрузки
.
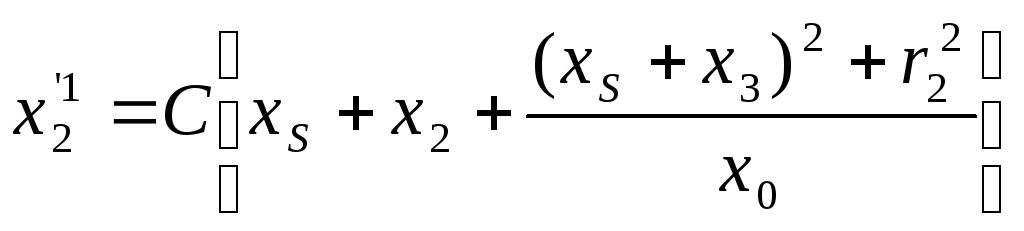(3.36)
=
0,35 · 10-3 Ом.
Эквивалентное активное сопротивление индуктора
r = r1 + r2. (3.37)
r = (0,01 + 0,23) · 10-3 = 0,24 · 10-3 Ом.
Эквивалентное реактивное сопротивление индуктора
х = х1 + х2. (3.37)
х = (0,20 + 0,23) · 10-3 = 0,43 · 10-3 Ом.
Полное сопротивление индуктора
.
(3.38)
= 0,50 · 10-3 Ом.
Электрический КПД индуктора
,
(3.39)
= 0,71
Определяем естественный коэффициент мощности по формуле
.
(3.40)
= 0,49.
Активная мощность индуктора
.
(3.41)
= 484015,6 Вт.
По активной мощности индуктора и частоте тока выбираем трансформатор ЭОМП-1600/10-82, мощность которого 630000 Вт.
Число индуктора
,
(3.42)
где U1 – напряжение на индукторе, U1 = 1750 В.
= 40.
Толщина
изоляции между витками индуктора
,
(3.43)
где ΔU1 – допустимый перепад напряжения на высоте индуктора, ΔU1=40000 В/м.
= 4,3...1,1 мм.
Принимаем толщину изоляции 4 мм. Ориентировочная высота индуктирующего витка
.
(3.44)
= 0,03 м.
По сортаменту выпускаемых промышленностью трубок выбираем трубку прямоугольного сечения. Определяем поперечное сечение канала охлаждения (внутреннее сечение)
SОХЛ = 0,03 · 0,05 = 0,0015 м2 = 1500 мм2.
Уточняем высоту индуктора
.
(3.45)
h1 = 0,03 · (40 + 1) + 40 · 0,004 = 1,39 м.
Активное сопротивление системы индуктор-загрузка
.
(3.46)
ru = 402 · 0,24 · 10-3 = 384 · 10-3 Ом.
Реактивное сопротивление системы индуктор-загрузка
.
(3.47)
xu = 402 · 0,43 · 10-3 = 688 · 10-3 Ом.
Полное сопротивление системы индуктор-загрузка
.
(3.48)
Zu = 402 · 0,50 · 10-3 = 800 · 10-3 Ом.
Ток индуктора
.
(3.49)
= 2187,5 A.
Линейная плотность тока в индукторе
.
(3.50)
= 62949,6
.
Плотность тока по сечению трубки индуктора
.
(3.51)
= 1
.
Плотность тока не превышает 20
.
Для увеличения коэффициента мощности cosφ путем компенсации реактивной индуктивной мощности применяют конденсаторные батареи. Емкость конденсаторной батареи
,
(3.52)
где Рρ – реактивная мощность индуктора
.
(3.53)
= 987,7 кВар.
= 1027,1 мкФ.
Для тигельных печей с напряжением более 1000 В выпускают специальные однофазные конденсаторы типа КСЭ мощностью РС = 75 кВа. Тогда потребное количество конденсаторов будет таким
= 13,7 шт.
Принимаем 14 конденсаторов.