Задание 1.

Построение и исследование физических моделей

Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мяча в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на определенном расстоянии.

Качественная описательная модель.

Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

• Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;

• Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с² и движение по оси ОУ можно считать равноускоренным;

• Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным.

Формальная модель. Для формализации модели обозначим величины:

• начальную скорость мячика- V₀

• угол бросания мячика- α

• высоту стенки- h

• расстояние до стенки- s

Изобразим график движения мячика:

Используем известные из курса физики формулы равномерного и равноускоренного движения. При заданной начальной скорости V₀ и угле бросания α значения координат дальности полета Х и высоты У от времени можно описать следующими формулами:

Чтобы определить, попадет ли мячик в стену, необходимо вычислить его координату Y в момент времени, когда он будет находиться на расстоянии s. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:

Подставляем это значение времени t в формулу для вычисления координаты Y. Получаем l- высоту мячика над землей на расстоянии s:

Формализуем условие попадания мячика в мишень. Попадание произойдет, если значение высоты l мячика будет удовлетворять условию неравенства:

Если l<0, то это означает «недолет», если l>h, то это означает «перелет».

Преобразуйте теперь формальную модель в компьютерную с использованием электронных таблиц Excel.

Модель «Движение тела, брошенного под углом к горизонту» в электронных таблицах

1. Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2.

2. Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.

3. В ячейки В5 и С5 введем формулы:

=$B$1*COS(РАДИАНЫ($B$2))*A5

=$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5

4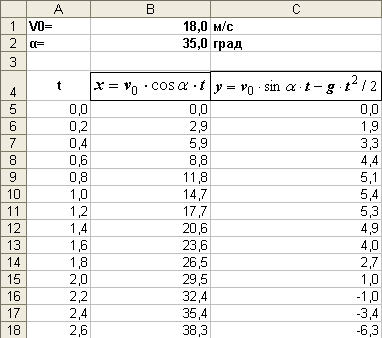. Скопируем формулы в ячейки В6:B18 и С6:С18 соответственно.

Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).

5. Построим диаграмму типа Точечная, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.

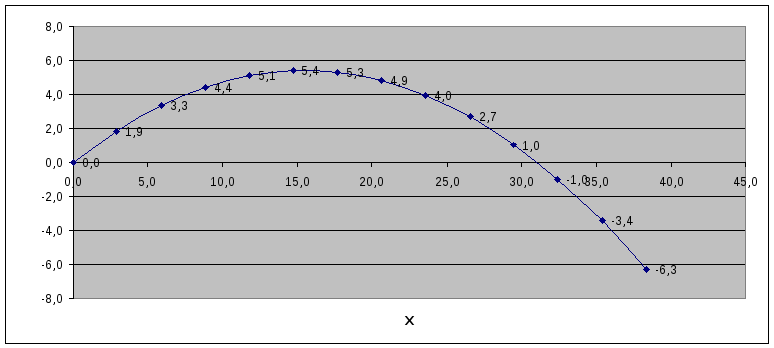
Исследование модели. Исследуем модель и определим с заданной точностью 0,1⁰ диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/С. Воспользуемся для этого методом Подбор параметра.

1. Установить для ячеек точность один знак после запятой.

2. Ввести в ячейки В21, В22 и В23 значения расстояния до мишени S=30 м, начальной скорости V₀ = 18 м/с и угла α=35⁰ , а в ячейку В25 – формулу для вычисления высоты мячика над поверхностью для заданных начальных условий:

=В21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(В23))^2).

Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.

3. Выделим ячейку В25 и введем команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели введем в поле Значение: наименьшую высоту попадания в мишень (то есть 0). В поле Изменяя значение ячейки: введем адрес ячейки, содержащей значение угла (в данном случай $B$23).

4. В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.

Таким образом, исследование модели показало, что существует диапазон значений угла бросания мячика от 32,6⁰ до 36,1⁰, при котором обеспечивается попадание в стенку высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.

Задание для самостоятельного выполнения:

определить диапазон предельных углов при начальном значении угла в ячейке B23, равном 55⁰.

Вывести на одном графике траектории мячика для двух диапазонов углов бросания.

Задание 2.

Приближенное решение уравнений в электронных таблицах

Постановка задачи

Найти корень уравнения приближенными методами (графическим и с помощью метода Подбор параметра).

Компьютерная модель

1. Представить заданное уравнении в табличной форме:

2. Для грубо приближенного определения корня построить диаграмму типа Точечная.

По графику грубо приближенно можно определить, что

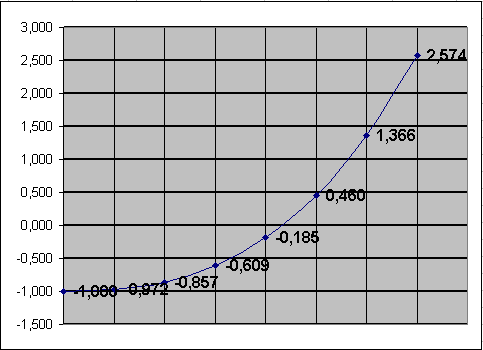
Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой).

Методом подбора параметра необходимо определить значение аргумента (ячейка F1), при котором значение функции (ячейка F2) будет равно нулю.

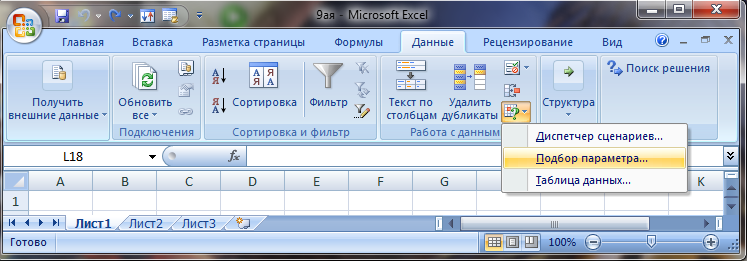
Выделить ячейку со значением функции F2 и ввести команду [На вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра.]

3. В диалоговом окне Подбор параметра:

• в поле Установить в ячейке ввести адрес ячейки $F$2

• в поле Значение ввести требуемое значение функции ( в данном случае 0)

• в поле Изменяя значение ячейки ввести адрес ячейки $F$1, в которой будет производиться подбор значения аргумента

• щелкнуть по кнопке ОК

4. На панели Результат подбора параметра будет выведена информация о величине значения в ячейке F2.

5. В ячейке аргумента F1 появится подобранное значение 0,855. Таким образом, корень уравнения 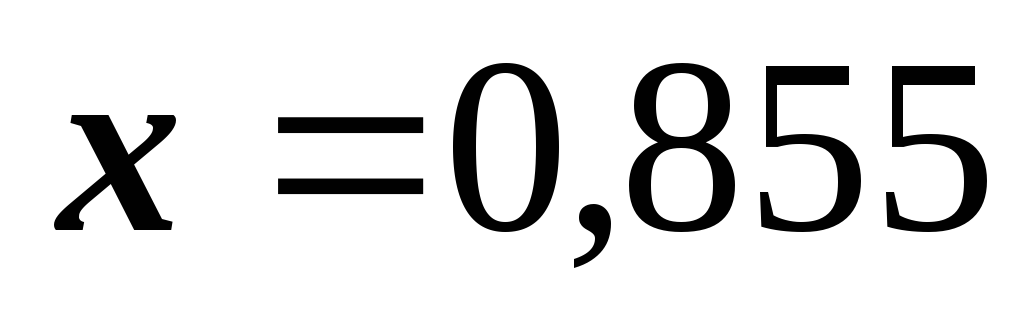найден с заданной точностью.

Задание для самостоятельного выполнения:

аналогичным способом решить уравнение

Задание 3.

Компьютерные модели развития популяций в электронных таблицах

Формальная модель

Начнём с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определённый процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста a:

Например, если ежегодный прирост численности популяции составляет 5%, то a=1,05

В модели ограниченного роста учитывается эффект перенаселённости, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением её численности.

Введём коэффициент перенаселённости b, значение которого обычно существенно меньше a. Тогда коэффициент ежегодного увеличения численности равен

В модели ограниченного роста с отловом, учитывается, что на численность промысловых видов животных и рыб оказывает влияние величина ежегодного отлова. Формула принимает вид:

Популяции обычно взаимодействуют с другими популяциями, наиболее важным является взаимодействие между хищниками и жертвами. В модели «хищник- жертва» количество жертв и количество хищников связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищником. В этом случае численность популяции жертв уменьшается на величину и формула для расчета численности жертв принимает вид:

Численность популяции хищников в отсутствие жертв ( в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой

,

где значение коэффициента d<1 характеризует скорость уменьшения численности популяции хищников.

Увеличение популяции хищников можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент g характеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать формулу: