Matematika_001

1. Линейное д.у.

y'+P(x)y=Q(x), y,y' только в 1-й степени

2. Однородные ур-ия

y'=f()

3. Д.у. Бернулли

y'+P(x)y=Q(x)yⁿ , n=1

4. Задача Коши с нач. условием

y(x₀)=y₀ - нач. условие

5. Д.у. с разделяющимися переменными

x√y dx-(1-x²)ydy=0

6. Задачу Коши требуется решать в ур-ии

y'=2^x-y, y(-3)=5

7. Линейное д.у. решается с помощью подстановки

y=u(x)*v(x)

8. Линейным д.у. яв-ся

x²y'-2xy-3=0

9. Линейным д.у. яв-ся

y'+ =arcsinx+x

10. Линейным д.у. яв-ся

y'+2yx=4x²

11. Линейным д.у. Яв-ся

xy'-y=x*cosx

12. Общий вид лин. д.у. 1 порядка

y'+M(x)y=N(x)

13. Общим видом ур-ия Бернулли

y'+M(x)y=N(x)yⁿ, n не равно1

14. Однородное д.у. Решается при помощи подстановки

y= tx

15. Однородным д.у. 1 порядка яв-ся

xy'sin+x=y*sin

16. Однородным у-ем 1 порядка яв-ся

y'= (1+)/(1-)

17. Решить задачу Коши требуется в ур-нии

+e^y=0, y(1)=0

18. Ур-ием Бернулли яв-ся

y'+=-xy²

19. Ур-ием Бернулли яв-ся

xy'+y=y²lnx

20. Ур-ием Бернулли яв-ся

y'=y+x√y

21. Частное решение следует искать в ур-ии

y'+=-y², y(0)=

22. Однородным д.у. яв-ся

y'=+cos

23. Общий вид д.у. с разделенными переменными

M(x)dx+N(y)dy=0

24. Общий вид д.у. с разделяющимися переменными M₁(x)M₂(y)dx+M₂(x)N₂(y)dy

25. Общий вид д.у. с разделенными переменными

dy=dx

26. Д.у. с разделяющимися переменными

y'cosx=(y+1)sinx (y'=dy/dx)

27. Общим решением д.у. (1+x²)dy-ydx=0 яв-ся

ln|y|=arctgx+C

28. Общим решением д.у. siny*sinx*dy=cosy*cosx*dx

Csinx*cosy=1

29. Решением д.у. y'+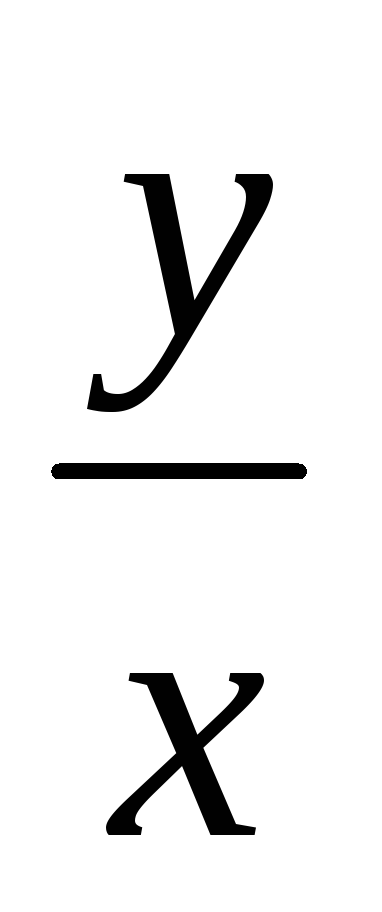=x яв-ся

y=+

30. Решением д.у. cosx*dx+dy=0

y=C-sinx

31. Решением д.у. y'=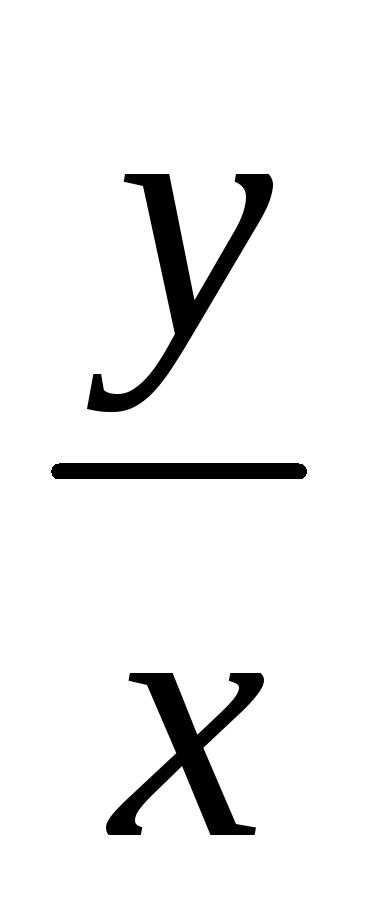+x²

y=x(C+)

32. Решением д.у. xy'=2y+2x⁴ яв-ся

y=x⁴+cx²

33. Решением д.у. y'=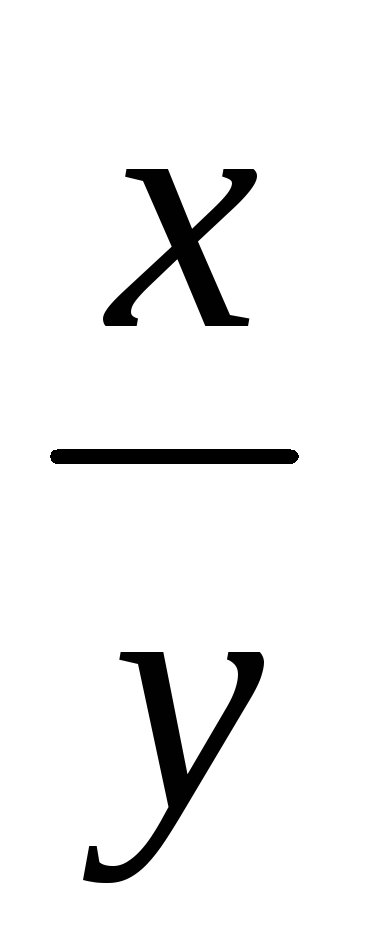+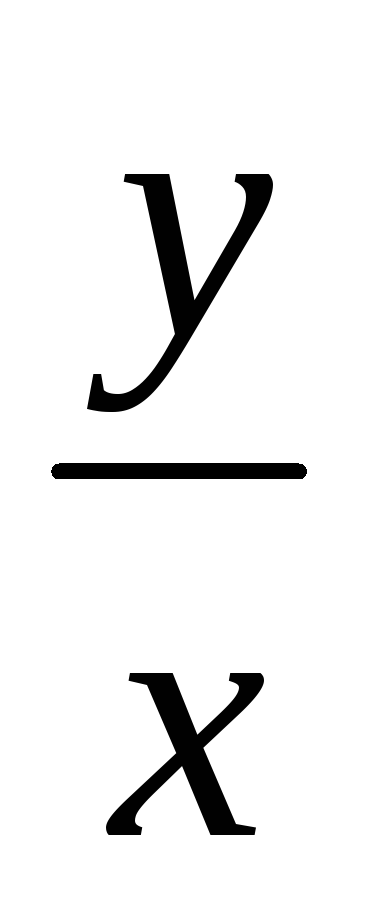яв-ся

y²=2x²ln|cx|

34. Решением ур-ия y'-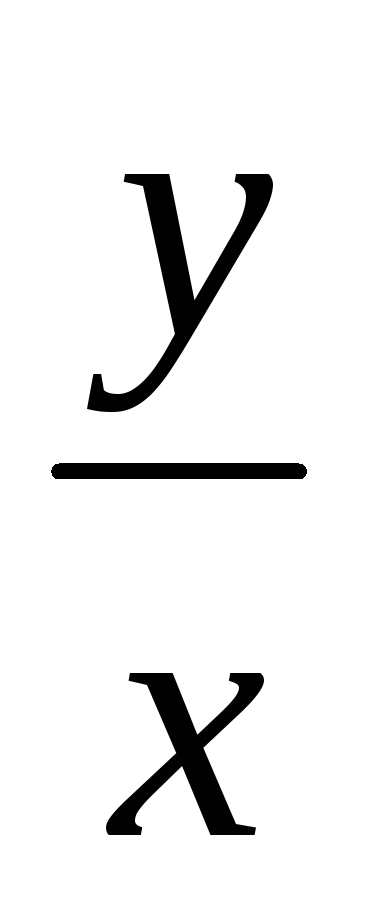=x² яв-ся

y=+Cx

35. Решением ур-ия 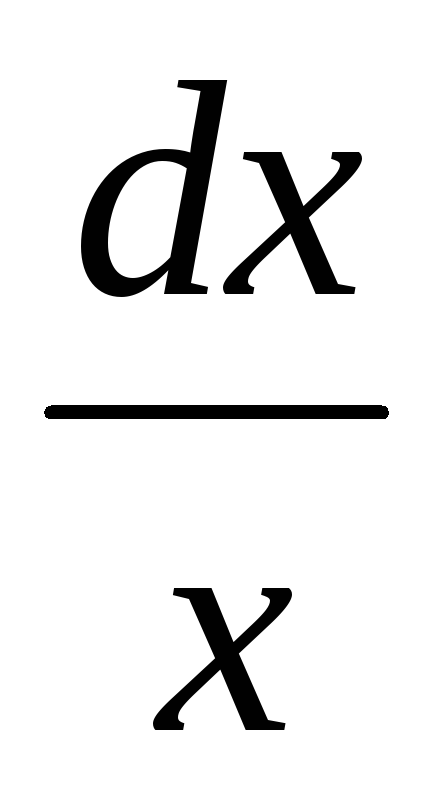-siny*dy=o яв-ся

ln|x|+cosy=C

36. Решением ур-ия y'=e+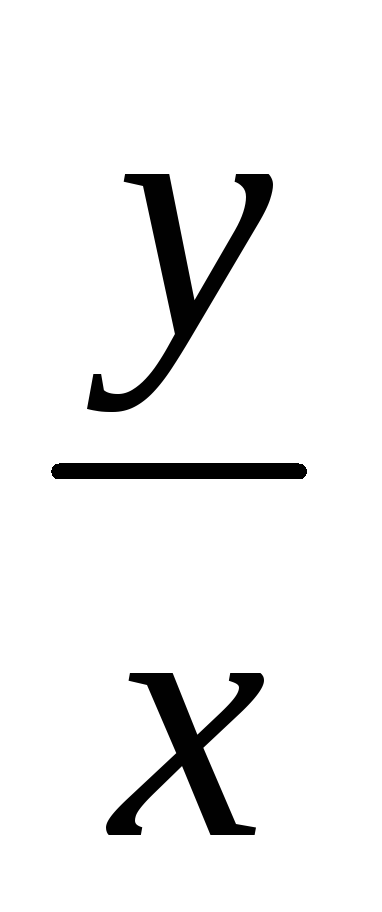яв-ся

e +ln|cx|=0

37. Решением ур-ия y'=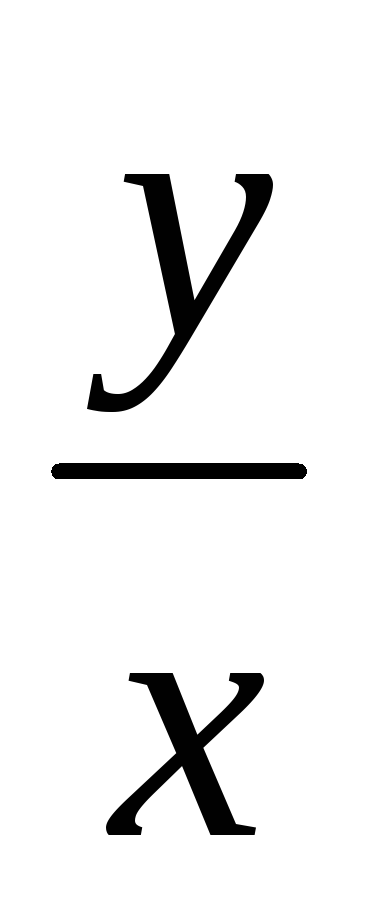+cos²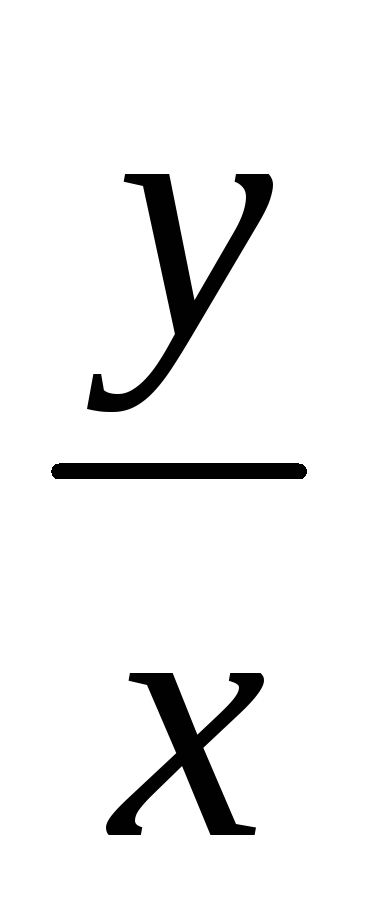яв-ся

tg=ln|cx|

38. Общим решением д.у. 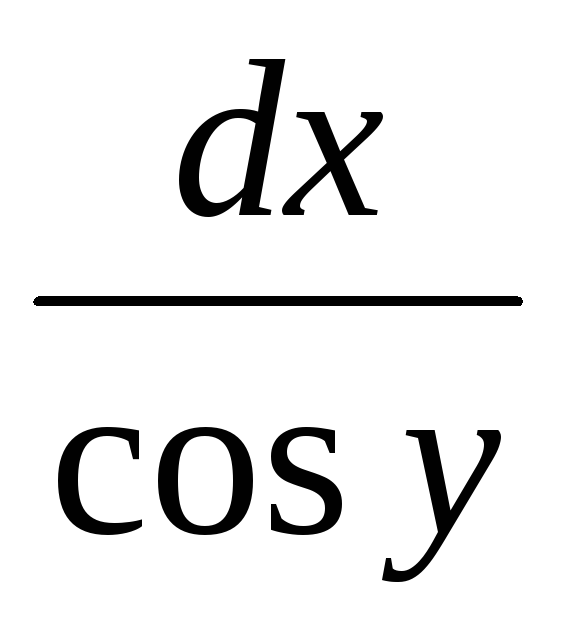- 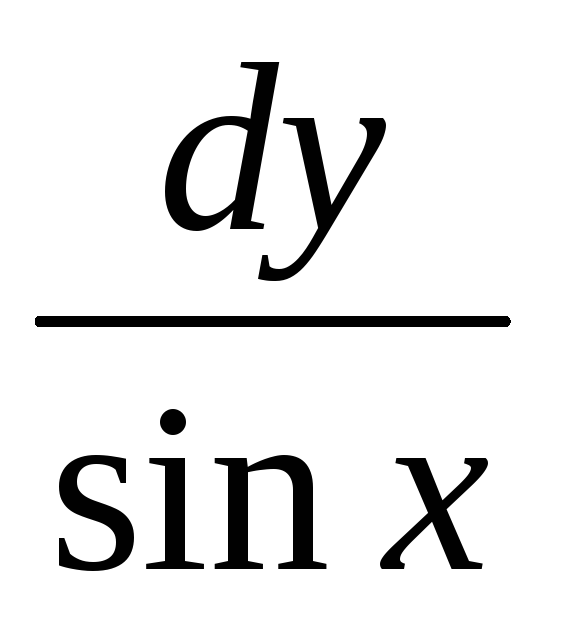=0 яв-ся

cosx+siny=С

39. Замена y'(x)=p(y) применяется в ур-ии

(y+y')*yⁿ+(y')2=0

40. Решением д.у. (xy²+x)dx+(y-x²y)dy=0

1+y²=C(1-x²)

41. Частным решением ур-ия y’=+x² при начальном условии y(1)=0.5 яв-ся

y=

42.Решением д.у. +dy=0 яв-ся

2x-3cosy=C

43. Частным решением ур-ия =, если y(1)=2 яв-ся

y=2x

44. Частным решением ур-ия -=0 при начальном условии y(1)=0 яв-ся

2=1-

45. Решением д.у. =0 яв-ся

tgx+arcsiny=C

46. Решением д.у. яв-ся

arcsinx-

47. Решением д.у. x²dx-=0 яв-ся

ln|y|=C

48. В ур-ии колебаний струны равно

49. Общим решением ур-ия яв-ся

50. Частным решением ур-ия xy’-y=xe^x при начальном условии y(1)=0 яв-ся

lnx+e=1

51. Общим решением ур-ия y’= яв-ся

y²=2x²lnCx

52. Решением д.у. xdx-y²dy=0 яв-ся

3x²-2y³=C

53. Общим решением ур-ия y’+=-xy² яв-ся

y=

54. Общим решением д.у. y¹¹-2y’-15y=0 яв-ся

y=C₁e^-3x+C₂e^5x

55. Общим решением ур-ия y’- яв-ся

y=

56. Решением д.у. dx+ яв-ся

x+2=C

57. Частным решением ур-ия y’=+x², если y(1)=0.5 яв-ся

y=

58. 1) абсолютно сходится

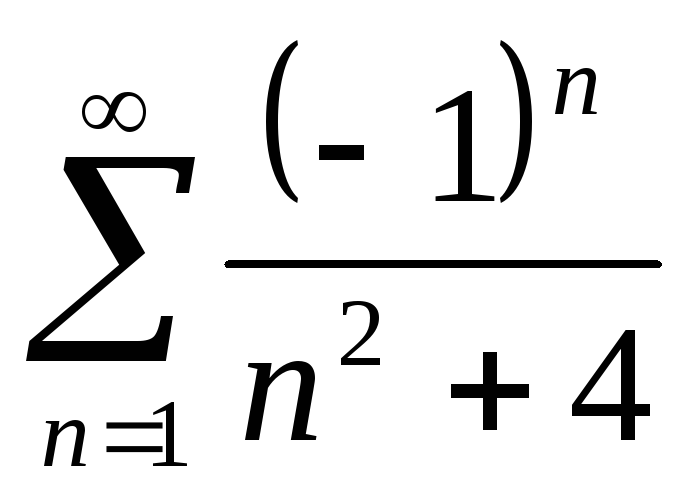
2)условно сходится

3)расходится

59. Законочередующимся яв-ся ряд

(-1+2-3+4…)

60. 1) абсолютно сходится

2)условно сходится

3)расходится

61. 1) абсолютно сходится

2)условно сходится

3)расходится

n!=1*2*3…n, где n-факторная

1!=1, 2!=1*2, 3!=1*2*3, 4!=1*2*3*4=24

62. 1) абсолютно сходится

2)условно сходится

3)расходится

63. 1) абсолютно сходится

2)условно сходится

3)расходится

64. 1) абсолютно сходится

2)условно сходится

3)расходится

65. Общий член последовательности 1, имеет вид

_n=

66. Общий член последовательности 1, равен

_n=

67. Пятый член последовательности 2, равен

₅=

68. Пятый член последовательности 1, равен

₅=

69. Пятый член последовательности 1, равен

₅=

70. Общий член последовательности 4, имеет вид

_n=

71. Четвертый член последовательности 1, равен

_n=

72. Общий член последовательности 1, равен

_n=

73. Пятый член последовательности имеет вид

₅=

74. Общий член последовательности имеет вид

_n=

75. Четвертый член последовательности 4, равен

₄=

76. Общий член последовательности 2, имеет вид

_n=

77. Сумма членов рядов равна

Сумма членов ряда равна 3

78. Сумма членов ряда равна

79. Сумма членов ряда равна 5

80. Сумма членов ряда равна

81. Сумма членов ряда равна 2,5

82. Для ряда суммы положительного члена тогда ряд сходится, если <1

83. F(x) одна из первообразных для ф-ции f(x). Тогда любая первообразная F(x) для ф-ции f(x) равна

ф(x)=f(x)+C

84. Одной из первообразных ф-ции f(x)=2x+1 яв-ся ф-ция F(x), равная

- x²+x+1

85. Одной из первообразных ф-ции F(x)=1-2x явл-ся ф-ция F(x), равная

x-x²+1

86. Одной из первообразных ф-ции F(x)=2-5x яв-ся ф-ция F(x), равная

-2,5x²+2x+1

87. Одной из первообразных ф-ции F(x)=3x-1 яв-ся ф-ция F(x), равная

1,5x²-x-1

88. Первообразная ф-ции F(x) для ф-ции f(x)=sinx, равна

-cosx+C

89. Первообразная ф-ции F(x) для ф-ции f(x)=x равна

+C

90. Первообразная ф-ции F(x) на интервале (a,b) наз-ся ф-ция F(x), если

F’(x)=f(x)

91. Соответствие неопределенных интегралов ф-иям:

1) ∫x²dx (α≠ -1) +C

2) ∫ ln|x|+C

3) ∫e^xdx e^x+C

4) ∫a^xdx +C

92. Соответствие первообразной F(x), ф-ции f(x)

1) F(x)= arccosx f(x)= -

2)F(x)=arcctgx f(x)=

3)F(x)= -cosx+C f(x)=sinx

4)F(x)=ctgx+C f(x)= -

93. Соответствие первообразной F(x), ф-ции f(x)

1) F(x)= arcsinx f(x)=

2)F(x)=arctgx f(x)=

3)F(x)= sinx+C f(x)=cosx

4)F(x)=tgx+C f(x)=

94. Соответствие первообразной F(x), ф-ции f(x)

1) arctg+C ∫

2) ln||+C ∫

3)arcsin ∫

4)ln|x+| ∫

95. Соответствие первообразной F(x), ф-ции f(x)

1) arcsinx+C ∫

2) arctgx+C ∫

3) ln||+C ∫

4)ln|x+| ∫

96. Соответствие первообразной F(x), ф-ции f(x)

1) –cosx+C ∫sinxdx

2)sinx+C ∫cosxdx

3)tgx+C

4) –ctgx+C 97. Соответствие

1)

2)

3)

4)

98. Соответствие

1)

2)

3)

4)

99. ∫lnxdx равен x(lnx-1)+C

100. ∫xe^-xdx равен -xe^-xe^-x+C

101. Форма интегрирования по частям ∫4dV равен uV-∫Vdu

102. Применяя формулу инт. по частям в интеграле ∫x²lnxdx u=lnx

103. Применяя формулу инт. По частям в интеграле ∫x²cos2xdx u=x²

104. Одной из первообразных ф-ций f(x)=x-1 явл. F(x), равное

105. ∫dx равен x+C

106. ∫0*dx равен C

107. ∫sin3xdx равен cos3x+c

108. ∫ равен ln|x±a|+C

109. ∫(3-x²)dx равен 3x+c

110. равен ln(x²+4)+C

111. ∫αxe сводится к табличному заменой t=x²

112. равен -+С

113. равен arctg(x+1)+C

114. равен

115. равен arctg+C

116. равен +C

117. равен ln|x²-4x+8|+C

118. равен |x²-4|+ln||+C

119. сводится к т..ному значению t=lnx

120. равен ln|x²-4x+5|+9arctg(x-2)+C

121. dSf(x)dx диф. Неопред. Интеграл равен f(x)dx

122. ∫cos2xdx равен sin2x+C

123. ∫sin²xcos²xdx равен -sin4x+C

124. равен ln-arctgx+c

125. равен tg²x+C

126. равен 2(-ln(+1))+C

127. равен ln|x-2|+ln|x+2|+C

128. ∫x²dx равен +С

129. ∫cos²dx равен sinx-sin³x+C

130.∫sin³xdx равен cos³x-cosx+C

131. ∫sin²2xdx равен x-sin4x+C

132. ∫ равен -+С

133. Определенный интеграл, выраженный площадью треугольника с вершинами (0,0),(2,0),(2,3) имеет вид

xdx

134. Опр. Инт., выраж. Площадью треуг. (0,0),(1,0),(1,2)

2xdx

134. Опр. Инт. S_∆ (0,0),(2,2),(2,0)

xdx

136. Площадь, ограниченная линиями y=12x-x² и y=0 равна 32

137. Площадь заштрихованной части фигуры

(( 2x-x²)-(-x))dx

138. Площадь заштрихованной части фигуры

(x-(x²-2x))dx