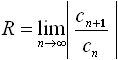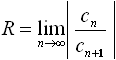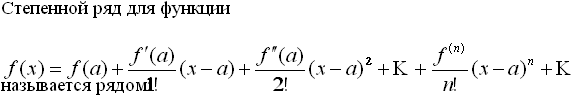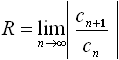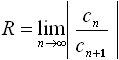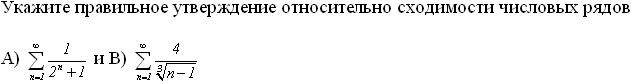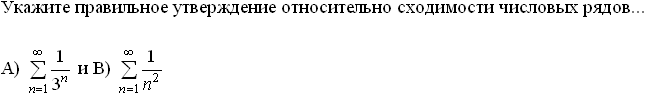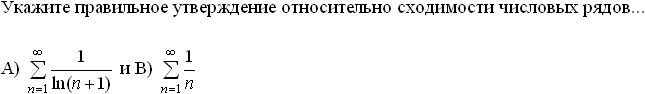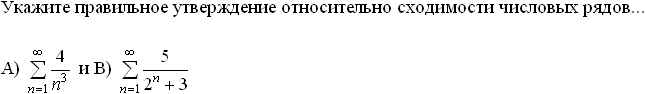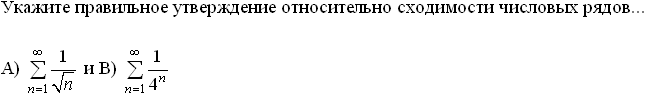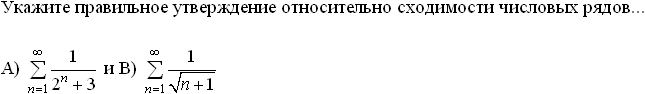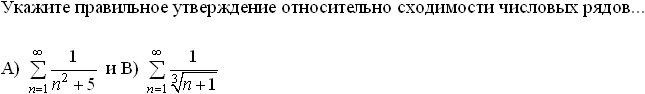17.11.2012 16:07

Дисциплина: "Математика" Дидактическая единица: "де_13_Последовательности и ряды. Степенные ряды_(у;мв,мт,мэ,мз,мо,эп,эм,амс,ат,смд,смэ,смн,э,д,гст;;)"

№   Вопроса	Вопрос
	№	Вариант ответа	Эталон ответа
1	Уровень: 1   Код:   423706/242760  (копия/оригинал) Задание: выбрать верные Абсолютно сходится знакопеременный числовой ряд, если ряд составленный из абсолютных величин его членов является ... 1 гармоническим - 2 вариационным - 3 расходящимся - 4 сходящимся +
2	Уровень: 1   Код:   423698/242757  (копия/оригинал) Задание: выбрать верные Абсолютно сходится ряд ... 1 - 2 - 3 - 4 +
3	Уровень: 1   Код:   423702/242762  (копия/оригинал) Задание: выбрать верные Степенным является ряд ... 1 - 2 - 3 - 4 +
4	Уровень: 1   Код:   423705/242749  (копия/оригинал) Задание: выбрать верные Сходящимся является ряд ... 1 - 2 - 3 - 4 +
5	Уровень: 1   Код:   423711/242748  (копия/оригинал) Задание: выбрать верные Сходящимся является ряд ... 1 - 2 - 3 - 4 +
6	Уровень: 1   Код:   423701/242758  (копия/оригинал) Задание: выбрать верные Условно сходится ряд ... 1 - 2 - 3 - 4 +
7	Уровень: 1   Код:   423717/104910  (копия/оригинал) Задание: определить соответствие Установите соответствие между знакопеременными рядами и видами сходимости: 1 абсолютно сходится 2 условно сходится 3 расходится 1 2 3
8	Уровень: 1   Код:   423718/104906  (копия/оригинал) Задание: определить соответствие Установите соответствие между знакопеременными рядами и видами сходимости: 1 абсолютно сходится 2 условно сходится 3 расходится 1 2 3
9	Уровень: 1   Код:   423719/104908  (копия/оригинал) Задание: определить соответствие Установите соответствие между знакопеременными рядами и видами сходимости: 1 абсолютно сходится 2 условно сходится 3 расходится 1 2 3
10	Уровень: 2   Код:   423703/107066  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
11	Уровень: 4   Код:   423714/107136  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
12	Уровень: 2   Код:   423713/107068  (копия/оригинал) Задание: выбрать верные 1 - 2 ln x - 3 - 4 +
13	Уровень: 2   Код:   423710/107139  (копия/оригинал) Задание: выбрать верные 1 (0; R) - 2 [- R; R] - 3 (-R; 0) - 4 (- R; R) +
14	Уровень: 2   Код:   423712/107067  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
15	Уровень: 3   Код:   423699/107137  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
16	Уровень: 2   Код:   423700/107064  (копия/оригинал) Задание: выбрать верные 1 Маклорена - 2 Фурье - 3 Лорана - 4 Тейлора +
17	Уровень: 3   Код:   423704/107138  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
18	Уровень: 2   Код:   423696/303480  (копия/оригинал) Задание: выбрать верные 1 (0; a + R) - 2 (- R; R). - 3 (a - R; 0) - 4 (a - R; a + R) +
19	Уровень: 1   Код:   423716/104899  (копия/оригинал) Задание: выбрать верные 1 -0,51 - 2 -2,1 - 3 2,1 - 4 0,51 +
20	Уровень: 1   Код:   423722/104900  (копия/оригинал) Задание: выбрать верные 1 -1,7 - 2 1,7 - 3 -0,8 - 4 0,8 +
21	Уровень: 1   Код:   423691/124962  (копия/оригинал) Задание: выбрать верные 1 (0;10) - 2 [-8;10] - 3 (-9;9) - 4 (-8;10) +
22	Уровень: 1   Код:   423674/124963  (копия/оригинал) Задание: выбрать верные 1 (-4;4) - 2 [-2;6] - 3 (0;6) - 4 (-2;6) +
23	Уровень: 1   Код:   423687/124959  (копия/оригинал) Задание: выбрать верные 1 (-5;5) - 2 [0;7] - 3 [-3;7] - 4 (-3;7) +
24	Уровень: 1   Код:   423677/124958  (копия/оригинал) Задание: выбрать верные 1 (-6;6) - 2 (0;7) - 3 (5;7) - 4 (-5;7) +
25	Уровень: 1   Код:   423683/124961  (копия/оригинал) Задание: выбрать верные 1 (-7;7) - 2 [-5;9] - 3 (-7;0) - 4 (-5;9) +
26	Уровень: 1   Код:   423693/124960  (копия/оригинал) Задание: выбрать верные 1 [-9;11] - 2 (-9;0) - 3 (0;10) - 4 (-9;11) +
27	Уровень: 1   Код:   423715/104915  (копия/оригинал) Задание: выбрать верные 1 А и В расходятся - 2 А - сходится, В - расходится - 3 А - расходится, В - сходится - 4 А и В сходятся +
28	Уровень: 1   Код:   423720/104916  (копия/оригинал) Задание: выбрать верные 1 А и В расходятся - 2 А - сходится, В - расходится - 3 А - расходится, В - сходится - 4 А и В сходятся +
29	Уровень: 1   Код:   423721/104912  (копия/оригинал) Задание: выбрать верные 1 А и В расходятся - 2 А - сходится, В - расходится - 3 А - расходится, В - сходится - 4 А и В сходятся +
30	Уровень: 1   Код:   423724/104911  (копия/оригинал) Задание: выбрать верные 1 А и В расходятся - 2 А - сходится, В - расходится - 3 А - расходится, В - сходится - 4 А и В сходятся +
31	Уровень: 1   Код:   423725/104913  (копия/оригинал) Задание: выбрать верные 1 А и В сходятся - 2 А и В расходятся - 3 А - расходится, В - сходится - 4 А - сходится, В - расходится +
32	Уровень: 1   Код:   423678/124927  (копия/оригинал) Задание: выбрать верные 1 А - сходится, В - расходится - 2 А - расходится, В - сходится - 3 А и В расходятся - 4 А и В сходятся +
33	Уровень: 1   Код:   423723/104914  (копия/оригинал) Задание: выбрать верные 1 А и В расходятся - 2 А - сходится, В - расходится - 3 А - расходится, В - сходится - 4 А и В сходятся +
34	Уровень: 1   Код:   423682/124928  (копия/оригинал) Задание: выбрать верные 1 А - сходится, В - расходится - 2 А - расходится, В - сходится - 3 А и В сходятся - 4 А и В расходятся +
35	Уровень: 1   Код:   423685/124930  (копия/оригинал) Задание: выбрать верные 1 А - сходится, В - расходится - 2 А и В расходятся - 3 А - расходится, В - сходится - 4 А и В сходятся +
36	Уровень: 1   Код:   423672/124929  (копия/оригинал) Задание: выбрать верные 1 А - сходится, В - расходится - 2 А и В расходятся - 3 А и В сходятся - 4 А - расходится, В - сходится +
37	Уровень: 1   Код:   423675/124926  (копия/оригинал) Задание: выбрать верные 1 А и В сходятся - 2 А - расходится, В - сходится - 3 А и В расходятся - 4 А - сходится, В - расходится +
38	Уровень: 1   Код:   423680/124931  (копия/оригинал) Задание: выбрать верные 1 А и В сходятся - 2 А и В расходятся - 3 А - расходится, В - сходится - 4 А - сходится, В - расходится +
39	Уровень: 2   Код:   423697/303481  (копия/оригинал) Задание: выбрать верные 1 - 2 - 3 - 4 +
40	Уровень: 1   Код:   423671/124951  (копия/оригинал) Задание: выбрать верные 1 1 - 2 4 - 3 0,25 - 4 0 +
41	Уровень: 1   Код:   423686/124952  (копия/оригинал) Задание: выбрать верные 1 1 - 2 -1 - 3 0,2 - 4 0 +
42	Уровень: 1   Код:   423692/124957  (копия/оригинал) Задание: выбрать верные 1 1 - 2 -1 - 3 0,5 - 4 0 +
43	Уровень: 1   Код:   423673/124955  (копия/оригинал) Задание: выбрать верные 1 1 - 2 0,25 - 3 -1 - 4 0 +
44	Уровень: 1   Код:   423694/124954  (копия/оригинал) Задание: выбрать верные 1 0,25 - 2 -1 - 3 1 - 4 0 +
45	Уровень: 1   Код:   423681/124953  (копия/оригинал) Задание: выбрать верные 1 0,25 - 2 -1 - 3 1 - 4 0 +
46	Уровень: 1   Код:   423670/124956  (копия/оригинал) Задание: выбрать верные 1 -1 - 2 1 - 3 0,2 - 4 0 +
47	Уровень: 1   Код:   423688/124944  (копия/оригинал) Задание: выбрать верные 1 -1 - 2 1 - 3 1,2 - 4 0,4 +
48	Уровень: 1   Код:   423689/124945  (копия/оригинал) Задание: выбрать верные 1 -1,3 - 2 1 - 3 -1 - 4 0 +
49	Уровень: 1   Код:   423684/124950  (копия/оригинал) Задание: выбрать верные 1 - 2 -1 - 3 1 - 4 +
50	Уровень: 1   Код:   423690/124946  (копия/оригинал) Задание: выбрать верные 1 -0,3 - 2 1 - 3 1,2 - 4 0,2 +
51	Уровень: 1   Код:   423679/124949  (копия/оригинал) Задание: выбрать верные 1 -0,5 - 2 -1 - 3 1 - 4 0,5 +
52	Уровень: 1   Код:   423676/124948  (копия/оригинал) Задание: выбрать верные 1 -1 - 2 1 - 3 1,2 - 4 0,4 +
53	Уровень: 1   Код:   423695/124947  (копия/оригинал) Задание: выбрать верные 1 -0,3 - 2 1 - 3 1,2 - 4 0,2 +

Общий член u_n ряда равен:

;

Общий член u_n ряда равен:

;

Сумма ряда равна:

2

Сумма ряда равна:

не существует

Условием сходимости для ряда условие является:

Необходимым

– последовательность частичных сумм ряда . Тогда ряд сходится, если предел равен:

S – конечное число

Ряд сходятся, а члены ряда , b_n  a_n. Тогда ряд :

Сходится

Ряд расходится, а члены ряда , b_n  a_n. Тогда ряд :

расходится

Ряд с положительными членами сходится если :

D < 1

Ряд :

Сходится

Ряд :

Расходится

Исследовать ряд на сходимость по интегральному признаку:

Сходится

Исследовать ряд на сходимость по интегральному признаку:

Расходится

Исследовать ряд на сходимость по радикальному признаку Коши:

сходится

Знакочередующийся ряд :

сходится

Ряд сходится абсолютно, если сходится ряд:

;

Радиус R сходимости ряда определяется по формуле:

;

Радиус R сходимости ряда определяется по формуле:

.

Интервал сходимости степенного ряда равен (R – радиус сходимости ряда):

( R; R)

R – радиус сходимости степенного ряда Тогда интервал сходимости ряда равен:

[a  R; a + R]; (a  R; a + R).

6.3.3.3/1

Область сходимости степенного ряда :

( 1; 1]

Степенной ряд для функции

называется рядом:

Тейлора

Степенной ряд для функции

называется рядом:

Маклорена

Ряд Маклорена является разложением в ярд функции:

e^x

Ряд Маклорена является разложением в ярд функции:

sin x

Ряд Маклорена является разложением в ярд функции:

cos x

Функциональный ряд вида в интервале ( ; ) называется рядом:

Фурье

равен:

0

равен:

0

Функция f (x), чётная в интервале ( ; ) разлагается в ряд Фурье по

Косинусам

Функция f (x), нечётная в интервале ( ; ) разлагается в ряд Фурье по

Синусам

Ряд является рядом Фурье для функции f (x) в интервале:

( ; )

i – мнимая единица. Тогда i² равно:

 1

Комплексное число z =  2 + 3i, Re z – действительная часть z – равна:

 2

Комплексное число z =  2i, Re z – действительная часть z – равна:

0

Комплексное число z =  2 + 3i, Im z – мнимая часть z – равна:

3 2

Комплексное число z = 3 + 2i, комплексно сопряжённое число равно:

3  2i

Комплексное число z =  i, комплексно сопряжённое число равно:

i

Комплексное число z = 3 + 4i, произведение равно:

25

Комплексное число z = 4 + 3i, модуль | z | комплексного числа равен:

5

Комплексное число , модуль | z | комплексного числа равен:

2

Комплексное число z = 1 + i, аргумент  = arg z комплексного числа равен:

Тригонометрическая форма комплексного числа :

;

Тригонометрическая форма комплексного числа :

Комплексные числа z₁ = 3 + 2i и z₂ =  1  i. Тогда сумма z₁ + z₂ равна:

2 + i

Комплексные числа z₁ = 4 + 3i и z₂ =  3 + 2i. Тогда разность z₁  z₂ равна:

7 + i

Комплексные числа z₁ = 3 + i и z₂ = 2  i. Тогда произведение z₁  z₂ равно:

7  i

Комплексные числа z₁ = 1  i и z₂ = 1 + i. Тогда частное равно:

 i

Комплексное число z = 1 + i. Тогда степень z⁸ равна:

16

Комплексное число . Тогда равен:

;

Значение функции f (z) =  z²  3i в точке z₀ = 1  2i равно:

3 + i

Значение функции f (z) = 2z²  i в точке z₀ = 1  3i равно:

 16  13i

Значение функции f (z) =  2z² + i в точке z₀ = 1 + 3i равно:

16 + 13i

Значение функции в точке z₀ = 2i равно:

равен:



равен:

0  

Для непрерывной функции f (z) в точке z₀ выполняется:

Производной функции f (z) называется функция f (z), равная:

Если функция f (z) = 5z²  7i, то значение производной этой функции в точке z₀ = 3  3i равно:

30  30i

Если функция f (z) = 2z²  5i, то значение производной этой функции в точке z₀ = 5  i равно:

20  4i

Если функция f (z) = 3z²  4i, то значение производной этой функции в точке z₀ = 4 + i равно:

24 + 6i

Для того, чтобы функция f (z) = u(x,y) + iv(x,y) имела производную в точке необходимо и достаточно, чтобы в этой точке выполнялись условия:

Однозначная функция называется аналитической в некоторой области при выполнении условия:

имеет производную в каждой точке

Функция f (z) = u(x,y) + iv(x,y), тогда интеграл равен:

Ряд называется:

рядом Лорана

Вычетом функции f (z) относительно изолированной точки однозначного характера (ИОТОХ-а) z = a является 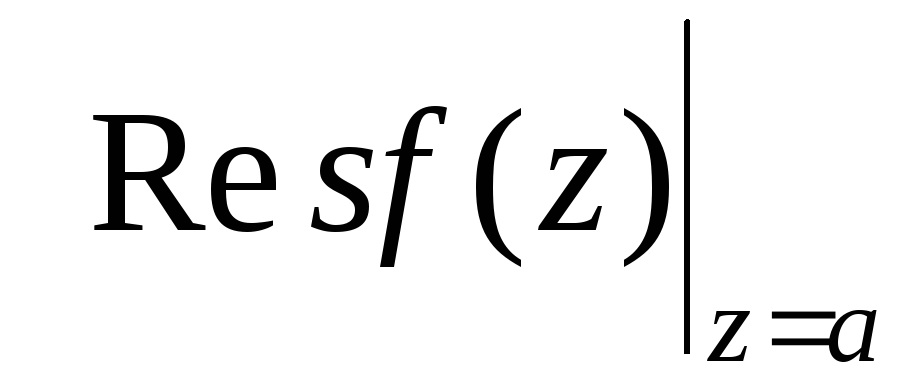, равный:

Вычетом функции f (z) относительно ИОТОХ-а z = a называется коэффициент c_n разложения f (z) в ряд Лорана по степеням (z  a), равный

c_1

Вычет функции относительно точки z = 0 равен:

2

Вычет функции относительно точки z = 1 равен:

6

, где C: | z | = 2 равен:

0

, где C: | z | = 1 равен:

Дифференциальным уравнением второго порядка является уравнение:

.(1-x²)-x=2

Общим решением уравнения (1+x²)dy+ydx=0 является:

. ln|y|=-arctgx+C

Дифференциальным уравнением с разделенными переменными является уравнение:

.

Общим решением уравнения является:

Общий вид дифференциального уравнения с разделенными переменными есть:

. M(x)dx+N(y)dy=0

Общим решением уравнения x²dx-=0 является:

.

Общим решением уравнения sinxdx+e^-3ydy=0 является:

. 3cosx+

Общий вид дифференциального уравнения с разделяющимися переменными есть:

.M₁(x)N₁(y)dx+M₂(x)N₂(y)dy=0

Дифференциальным уравнением с разделяющимися переменными является уравнение:

(y+1)sinx

Общим решением уравнения =2^x-y является:

2^y=2^x+C

Общим решением уравнения sinysinxdy = cosycosxdx является:

Csinxcosy=1

Общим решением уравнения является:

Решить задачу Коши требуется в уравнении:

.

Частным решением уравнения при начальном условии у(1)=0 является:

Частным решением уравнения при начальном условии у(1)=0 является

Частным решением уравнения при начальном условии у(1)=0,5 является:

y=

Частным решением уравнения при начальных условиях у()= является:

. 2y²-4x²=1

Однородным дифференциальным уравнением 1 порядка является уравнение:

.

Однородное дифференциальное уравнение 1 порядка решается при помощи подстановки

y=

Общим решением уравнения является:

.

Частным решением уравнения при начальном условии y(1)=0 является:

Общим решением уравнения является:

.

Общий вид линейного дифференциального уравнения 1 порядка есть:

Линейным дифференциальным уравнением 1 порядка является уравнение:

.

Линейное дифференциальное уравнение решается при помощи подстановки

.

Общим решением уравнения является:

Общим решением уравнения является:

Общим видом уравнения Бернулли является:

Уравнением Бернулли является уравнение

.

Общим решением уравнения является:

Общим решением уравнения является:

Замена применяется в уравнении

Общим решением уравнения является:

К дифференциальному уравнению вида

относится уравнение

Общим решением дифференциального уравнения является:

Замена применяется в уравнении

К дифференциальному уравнению вида

относится уравнение

Общим решением уравнения является:

Общим решением уравнения является:

Дифференциальное уравнение относится к виду

.

Линейным однородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение:

.

К линейному однородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:

Общим решением дифференциального уравнения является:

Общим решением дифференциального уравнения является:

.

Общим решением дифференциального уравнения является:

Общим решением дифференциального уравнения является:

.

Общим решением дифференциального уравнения является:

Линейным неоднородным дифференциальным уравнением 2 порядка с постоянными коэффициентами называется уравнение:

.

К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:

Частное решение дифференциального уравнения ищется в виде:

Частное решение дифференциального уравнения ищется в виде:

.

Частное решение дифференциального уравнения ищется в виде:

Решение дифференциального уравнения ищется в виде

Решение дифференциального уравнения ищется в виде , где

Частное решение дифференциального уравнения ищется в виде:

.

К линейному неоднородному дифференциальному уравнению 2 порядка с постоянными коэффициентами относится уравнение:

Решение дифференциального уравнения ищется в виде

.

Линейной неоднородной является система

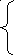
В уравнении колебаний струны a² равно

.

В уравнении колебаний струны равно

Уравнением свободных колебаний струны является

Решением уравнения , , является

.

Линейной системой второго порядка является

.

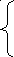
Линейной системой второго порядка является

.

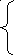Линейная система дифференциальных уравнений

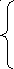
называется однородной, если:

Однородной линейной системой первого порядка является

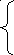
Неоднородной линейной системой является

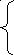
Частное решение требуется найти в системе

. x(0)=2

y(0)=0

Решением дифференциального уравнения является:

Решением дифференциального уравнения является:

.

Решением дифференциального уравнения является:

Решением дифференциального уравнения является:

.

Решением дифференциального уравнения является:

Дифференциальным уравнением с разделяющимися переменными является:

.

Решением дифференциального уравнения является:

Решением дифференциального уравнения является:

.

Решением дифференциального уравнения является:

.

Решением дифференциального уравнения является:

.

Задачу Коши требуется решить в уравнении

Задачу Коши требуется решить в уравнении

Частным решением уравнения при условиях у(0)=0, является

Частным решением уравнения , если y(1)=2 является

.

Частным решением уравнения , если является

.

Частное решение следует искать в уравнении

. ;

Однородным уравнением первого порядка является

.

Решением уравнения является

.

Решением уравнения является

Решением уравнения является

Линейным дифференциальным уравнением является

Линейным дифференциальным уравнением является

.

Линейным дифференциальным уравнением является

.

Решением уравнения является

.

Решением уравнения является

Уравнением Бернулли является

Уравнением Бернулли является

.

Решением уравнения является

Решением уравнения является

Решением уравнения является

Решением уравнения является

Частное решение уравнения ищется в виде:

Однородным уравнением первого порядка является

Дано: z₁ =1 -3i ; z₂ = 2 + i, тогдаравно ...

Аргумент комплексного числа -3+3i равен...

Если z₁ =2-i, z₂ = 3+i ,то z₁∙z₂ равно...

7-i

Дано: z₁=6+i; z₂=1-2i, тогда равно ...

Если z₁=1-i, z₂=3+i, то z₁∙z₂ равно...

4-2i

Аргумент комплексного числа -1+i равен ...

Аргумент комплексного числа -1+i равен...

Если z₁=2+3i, z₂=5-i, то z₁∙z₂ равно...

13+13i

Дано z₁=3+i, z₂=2-i, тогда равно...

1+i

Если z₁ =2-i, z₂ =l + i, то z_1∙z₂ равно...

3+i

Дано: z₁=6-i, z₂=1+2i, тогда равно...

Аргумент комплексного числа равен ...

Аргумент комплексного числа равен ...

Дано: z₁=2+i, z₂=1-i, тогда равно...

Если z₁=2-i, z₂=1+i, то z₁∙z₂ равно...

З+i

Если z₁ =1+2i, z₂ =2-i ,то z₁∙z₂ равно...

4+3i

Дано: z₁=4+i, z₂=1-i, тогда равно...

Дано: z₁=2-i, z₂=1+i, тогда равно...

Если z₁=2-3i, z₂=3-i, то z₁∙z₂ равно...

3-11i

Дано z₁=1-i, z₂=2+i, тогда равно...

Если z₁=3-i, z₂=2-i, то z₁∙z₂ равно...

5-5i

Значение y(x) при x=2, где y(x) - решение задачи Коши , равно ...

2

Если y(x) решение задачи Коши , то y(2) равно ...

2

Если y(x) решение задачи Коши , то y(1) равно ...

Значение y(x), при x=2, где y(x) - -решение задачи Коши равно ...

2

Значение y(x), при x=1, где y(x) - решение задачи Коши равно ...

Если y(x) решение задачи Коши y(0)=1, то y(1) ...

e

Значение y(x) при x=2, где y(x) - решение задачи Коши (1+x)dy+ydx=0,y(0)=1,) равно ...

1/3

Значение y(x) при x=2, где y(x) - решение задачи Коши равно ...

Общее решение дифференциального уравнения , имеет вид ...

Общее решение дифференциального уравнения , имеет вид ...

Общее решение уравнения имеет вид ...

Если, тогда значение производной этой функции в точке равно...

16+40i

Если f(z)=4z²-10i, тогда значение производной этой функции в точке z₀=1-3i равно...

8-24i

Если f(z)=3z²-9i, тогда значение производной этой функции в точке

z₀=5+7i равно...

30+42i

Если f(z)=5z²-7i, тогда значение производной этой функции в точке z₀=3-3i равно ...

3-3i

Установите соответствие между знакопеременными рядами и видами сходимости.

абсолютно сходится

условно сходится

расходится

Если f(z) =_6z² –i, тогда значение производной этой функции в точке z₀ = l + 2i равно...

12+24i

Если f(z)=2z²+15i, тогда значение производной этой функции в точке z₀=1-4i равно...

4-16i

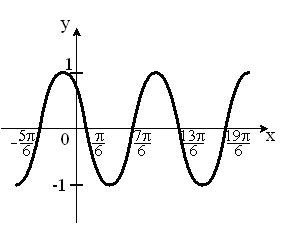
Укажите вид графика периодической функции ...

Если f(z)=4z²-9i, тогда значение производной этой функции в точке z₀=1-i равно ...

8-8i

Если f(z)=4z²-i, тогда значение производной этой функции в точке z₀=1+5i равно...

8+40i