5.6. Физическое моделирования узла трения (на примере пары трения «колесо – рельс»)

На сегодняшний день трудно представить единую методику моделирования, которая бы позволила создать цельную модель путевой машины, включающую единство подсистем конструкции рамы с навесным оборудованием, систем подвески и собственно колесной пары и тягового привода, так и модель верхнего строения пути. Каждая из данных подсистем может быть представлена в виде физической или математической модели. Общим правилом разделения подсистем может быть наличие в ней узла трения, роль которого в данной подсистеме является определяющей, то есть оказывающей определяющее влияние на динамику ее функционирования. Например, пара сцепления «колесо – рельс», демпферы крутильных и линейных колебаний, тормоза, фрикционная муфта и т.д.

Практически все системы можно определить как фрикционные механические системы, потому что уже наличие крепежных узлов (пара болт – гайка – шайба, заклепка и т.д.) ставят их функционирование в зависимость от трения. Придавая им статус стабильного узла трения (оптимально высокое и стабильное значение коэффициента сцепления, контроль затяжки болтовых соединений, наличие устройств компенсации зазоров, гарантированная работоспособность подшипников трения качения и гидродинамических подшипников скольжения) на время эксплуатации или межремонтный цикл.

Поэтому закономерности движения, проблемы управления движением необходимо рассматривать с учетом заданных и изменяющихся в ходе эволюции свойств фрикционного контакта.

Изучение фрикционных механических систем как механической системы не всегда возможно и корректно, поскольку различные входящие в нее подсистемы определяются различными физико-механическими, химическими и физическими взаимодействиями и не вписываются исключительно в проблемы механики систем.

Достоверность модели фрикционной части ФМС имеет принципиальное значение, так как она объединяет упруго-диссипативные характеристики механических подсистем, строго говоря, не описываются ни одной из моделей классической механики, так как они зависят от мощности и работы диссипативных сил и относятся исключительно к проблемам нелинейной механики. Однако, наличие такого специфичного состояния фрикционного контакта, как установившийся после приработки процесс равновесного состояния позволяет характеризовать его как случайно-стационарный, то есть диссипативные свойства, свойства пограничных слоев и трибоконтакта остаются переменными во времени, однако эти изменения являются достаточно медленными.

Представление путевой машины как пространственной дискретной динамической структуры взаимодействующих подсистем, определенные массы которых взаимодействуют через упруго-диссипативные связи, получил в динамике машин большее распространение и фактически является предметом исследования теории колебаний систем с конечным числом степеней свободы. Тем не менее, необходимо учитывать, что как подсистемы, так и все разнообразные процессы, протекающие в них (преобразование энергии механической системы в производство тепла, в работу сил трения на перемещение и т.д.) являются взаимосвязанными и одновременно частично самостоятельными.

Поэтому при составлении физико-математической модели исследуемой системы необходимо учитывать, что:

• подсистема сцепления является тем фактором, который объединяет упруго-диссипативные характеристики механических подсистем машины в единую динамическую ФМС;

• свойство взаимосвязи подсистем в полной мере не описываются ни одной из моделей классической механики, так как они зависят от мощности и работы диссипативных сил;

• контактирующие тела колесо и рельс считаются недеформируемыми, их возможные пространственные смещения определяются исключительно действием упруго-диссипативных связей, наложенных на движения сосредоточенных масс;

• для динамической ФМС параметры упруго-диссипативной системы являются переменными;

• в единой динамической системе все физико-механические и механо-химические процессы являются взаимосвязанными и одновременно обладают некоторой самостоятельностью.

Процессы сцепления являются существенно нелинейными. Поэтому наиболее достоверные результаты при исследовании данных задач дают методы оценки определяющих процессов и явлений через модельный эксперимент. Физическое моделирование процессов реализации сил сцепления в контакте «колесо – рельс» при воздействии сил, перемещений и колебаний подвижного состава, а также динамического отклика на данное воздействие со стороны элементов ВСП можно реализовать, используя основные положения теории моделирования [1, 4, 22, 23].

Метод анализа размерностей, с введенными условиями динамического подобия, позволяет сложные неоднородные системы превращать в сложные однородные и получать единственное значение масштабных коэффициентов перехода от модели к натуре для каждого из параметров.

При комплексном моделировании, на этапе моделирования механического, теплового и динамического подобия механических систем, необходимо учесть ограничения, определяющие как динамику механической системы без пары сцепления «колесо – рельс» и условия ее определяющие, так и тождественность аналогичных процессов механической части модели и натуры, в том числе коэффициента затухания гармонических составляющих (форм собственных колебаний) модели и натурных поверхностей колеса и рельса.

В системе основных единиц выбираются четыре параметра (базисные), которые оказывают существенное влияние на исследуемый процесс, это [8, 24] скорость каченияV, осевая нагрузка, коэффициент теплоотдачи, линейные размеры. В качестве краевых условий выбираем температуру в зоне сцепления пары «колесо – рельс», контактное давление, время, то есть, что достигается применением одинаковых параметров натурного образца и модели.

Расчет масштабных коэффициентов перехода от натурного образца к модели производится по разработанной программе "MKP". Результаты представлены в виде скриншота реализации программы расчета масштабных коэффициентов перехода от натуры к модели.

С точки зрения возможности анализа получаемых результатов большой интерес представляет расчет масштабных коэффициентов вручную, так как при моделировании по программе "МКР" невозможно выделить промежуточные результаты расчета, в частности, получаемые константы подобия для моделируемых величин. Результаты расчетов представлены в таблице 5.2.

Базисный определитель будет иметь вид

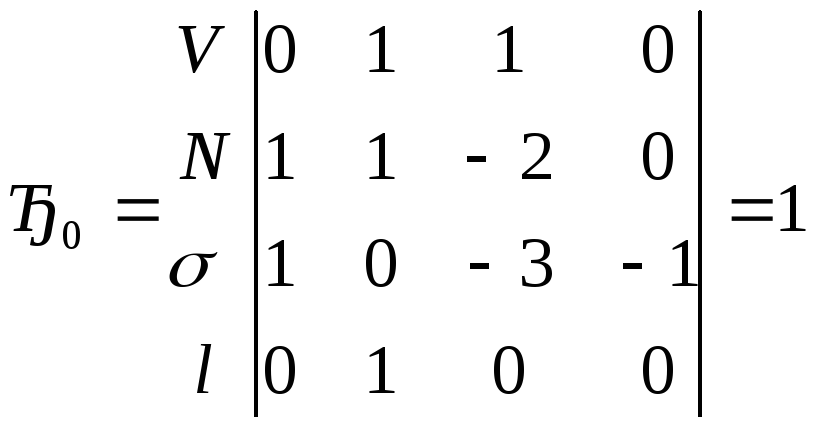
Заменяя поочередно строки в базисном определителе на строку с размерностью параметра, для которого определяется индикатор подобия, получаем четыре определителя , то есть для параметракритерий подобия будет иметь вид

Объединим с параметрами базисного определителя параметры процесса:

1) Сопротивление срезу пленок - Т

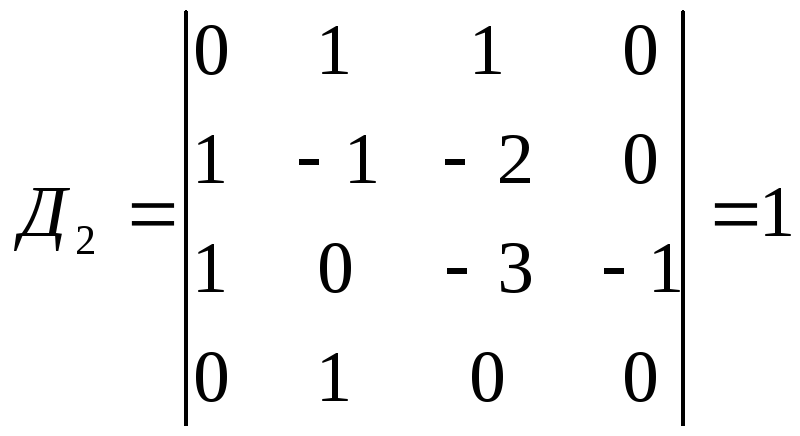
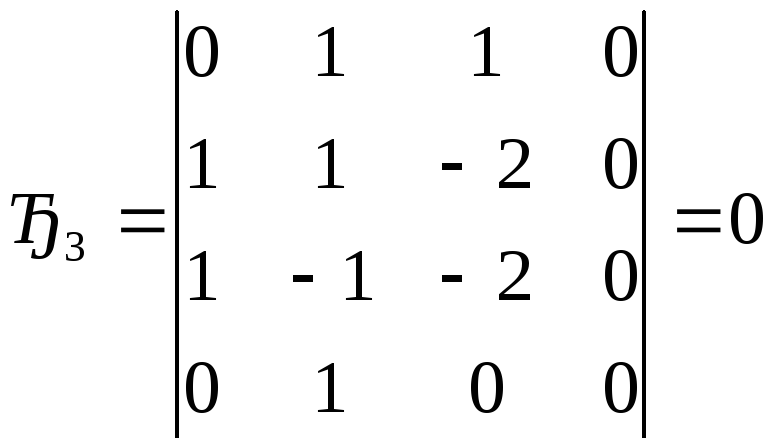
( 5.32)

Аналогичным образом связываются с базисными параметрами все остальные параметры процесса трения , принятые для моделирования.

1) Демпфирование 

( 5.33)

2. Масса

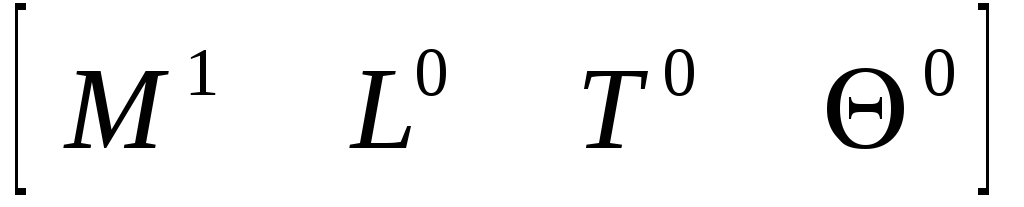
(5.34)

2. Момент инерции I

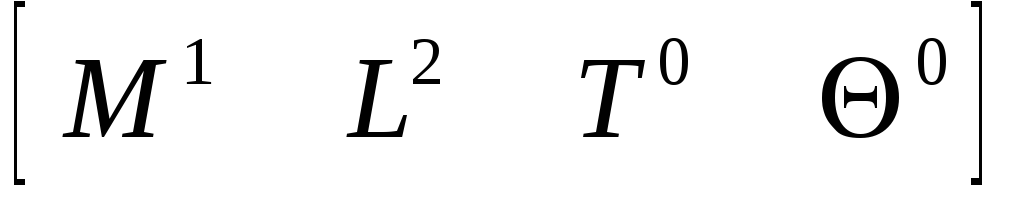
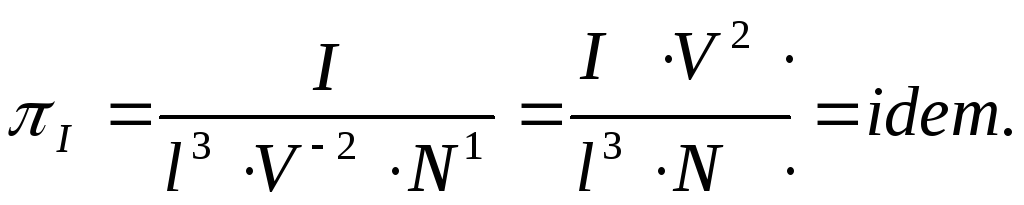(5.35)

2. Круговая жесткость

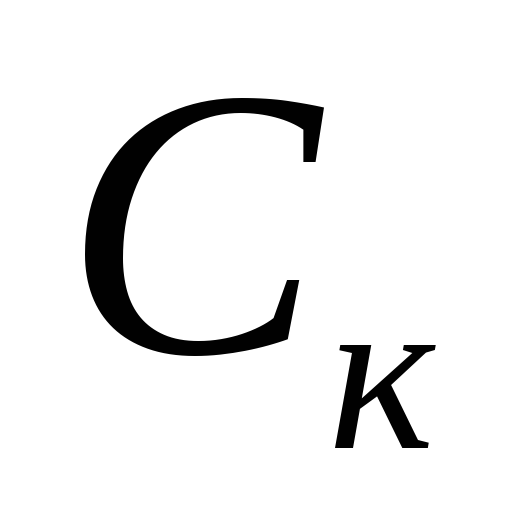
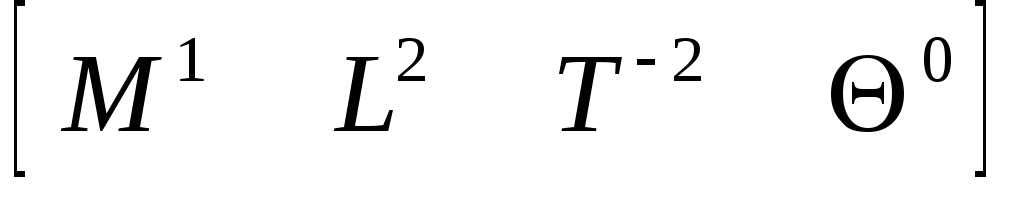
(5.36)

2. Площадь сцепления колеса и рельса Aa

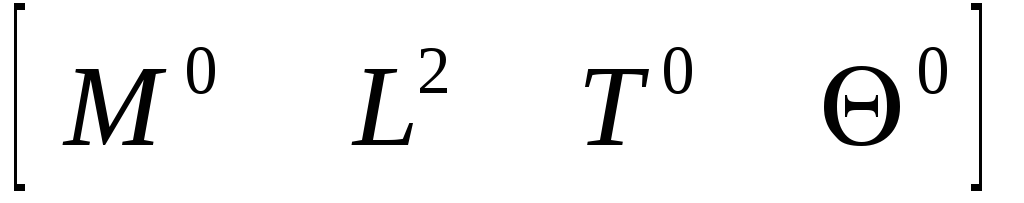
(5.37)

2. Сила сцепления F

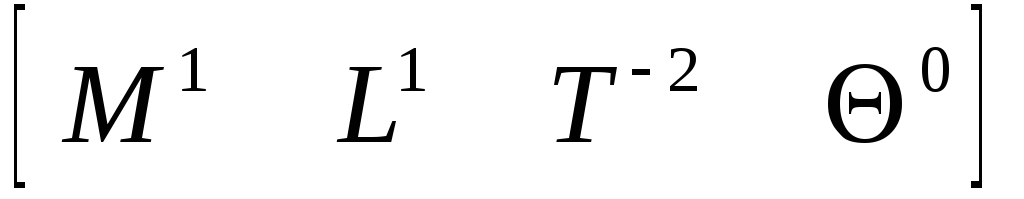
(5.38)

2. Частота колебаний 

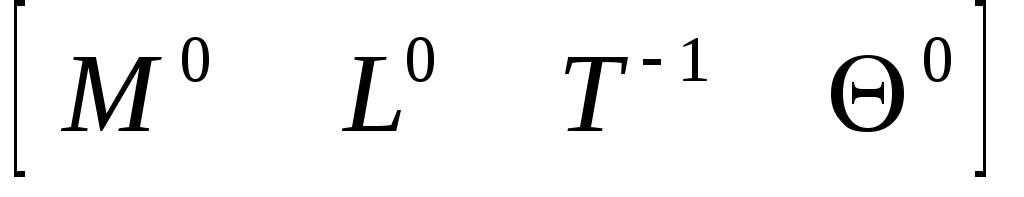
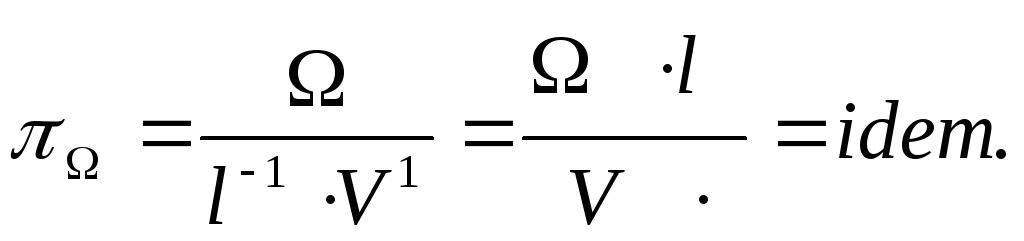(5.39)

2. Динамическая вязкость загрязнителей M

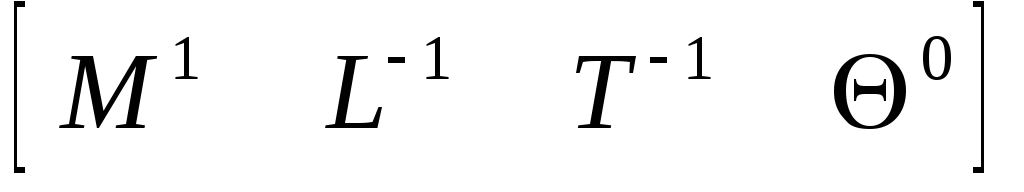
(5.40)

2. Твердость НВ

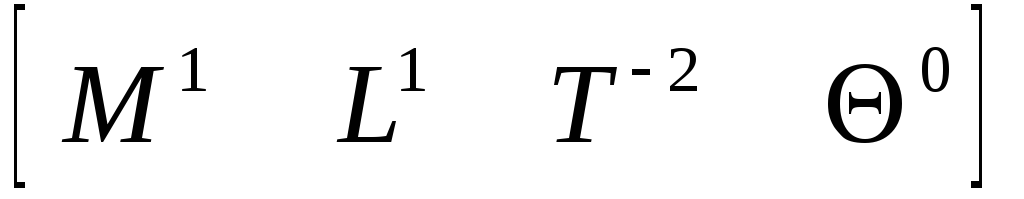
(5.41)

2. Время t

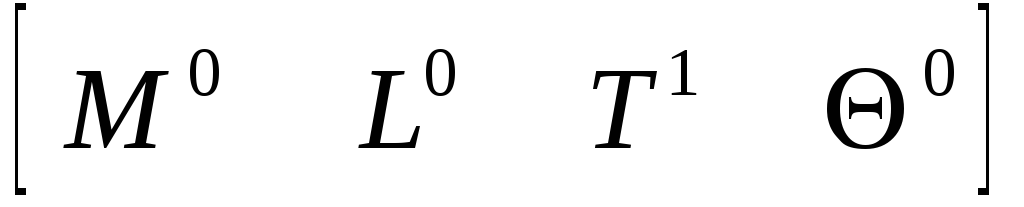
( 5.42)

2. Температура

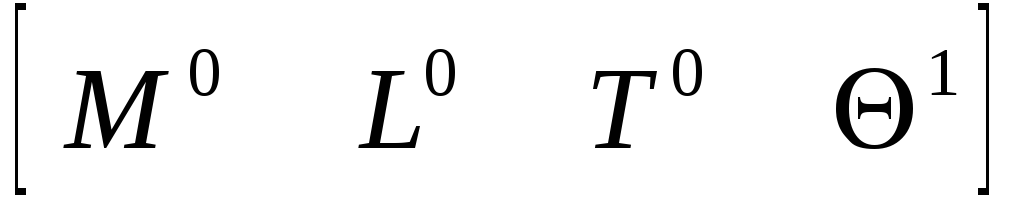
( 5.43)

Уравнение подобия, объединившее полученные критерии, состоит из 14 критериев, так как, согласно теореме Бэкингэма, должно быть равно числу параметров за вычетом четырех базисных.

. ( 5.44)

Таблица 5.2 - Характеристики и константы подобия

Характеристика	Обозна- чение	Размерность в системе М LT	Обозначение по програм- ме "МКП"	Константа МКП
Скорость качения	V		V
Коэффициент теплоотдачи			CG
Жесткость линейная	C		Cl
Сопротивл. срезу пленок	T		T
Демпфирование			B
Масса	m		m
Момент инерции	J		J
Жесткость крутильная			Ck
Площадь сцепления	S		AA
Сила сцепления	F		F
Частота колебаний			Y
Твердость	HB		HB
Динамич. вязкость загрязнителей	M		M
Температура объемная			
Время трения	t		t
Контактное давление	q		q
Градиент температуры	S		S

Для проверки полученных критериев подобия, составляющие критериальное уравнение (5.44), воспользуемся их сопоставлением с критериями многократно апробированы при исследованиях аналогичных процессов в других областях техники.

Рассмотрим несколько разнородных критериев, характеризующих соотношения силовых, теплофизических процессов и процессы работы при наличии третьего тела (загрязнителей) на поверхности сцепления пары «колесо – рельс»:

1. Критерий гомохронности, характеризующий однородность процессов во времени: , гдеV- скорость,t- время,L- путь, в реализованном моделировании получается, если критерий времени (5.32) разделить на критерий пути трения (2.37), то есть.

Так как в выражение критерия гомохронности входят параметры V,t,L, то даже если ни один из этих параметров не входит в число базисных, перемножение критериев скорости и времени и деление на критерий пути в результате обеспечивает получение критерия гомохронности.

2. Критерий силы сцепления (5.38) умножим на критерий времени (5.42) и разделим на критерий массы (5.34 ):

или, подставляя вместо , в результате получаем критерий Ньютона.

3. Критерий массы (5.34 ) разделим на критерий времени (5.42): , подставляя вместои, получаемили, умножив на квадрат критерия гомохронности, получаем- критерий Фруда.

4. Критерий температуропроводности (5.34) разделим на критерий пути (5.37) трения: или заменяя, получаем- критерий Фурье.

5. Критерий пути (5.37) разделим на критерий теплопроводности (5.42):

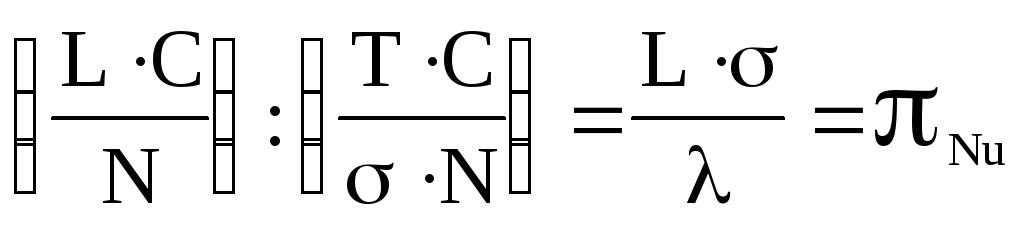- критерий Нуссельта.

159